C++/编译原理语法分析：求解First集合

Posted 2021-10-14 立秋小猪

上机要求

• 目的：熟练掌握自上而下的语法分析方法，并能用程序实现。

• 要求：
  例如，使用的文法如下：
  编写First函数，实现其求解过程。

  E -> TE\'
  E\' -> +TE\' | #
  T -> FT\'
  T\' -> *FT\' | #
  F -> (E) | id
  end

• 提示：

  1. 非终结符为 大写字母；或 后面带’的大写字母
  2. 终结符为 小写字母和符号（+、*）
  3. 推导符号→为或->
  4. 用end结束文法。

• 不针对特定文法，编写求first函数。

原理

• A -> a， 则将 a 加入 First(A)中
• A -> Y₁Y₂···Y_n
  将 First(Y₁) 除空串外的字符加入到First(A)中，若 1 =< i < n - 1，Y₁，Y₂， Y_i中均含有空串，则将First(Y_{i + 1})加入到First(A)中，若Y₁，Y₂，···，Y_n都有空串，则将空串加入到First(A)中
• First(a) = {a}

一点思路及优化

• 将输入格式化（扫描输入）
• 将产生式转换为哈希map：
  对任一产生式： A -> body_1 | body_2 | ··· | body_n，
  将 A 作为map的 key，
  map的value为一个string类的向量(vector<string>)，
  将 body_1，body_2，···，body_n 都加入value中。
• 求解First(str)
• 特殊情况处理，str为空或str不在产生式的key中，返回空；str的首个字符是终结符，返回首个字符构成的集合。
• 一般情况，获取str推导产生的产生体集bodys(其中的每个产生体为body)，遍历产生体集合求解First集
• 针对空串，我们加入标记hasBlank = true，往下遍历body的字符
• body的首个字符为终结符，直接将该字符加入first集，记hasBlank = false以便遍历下一body（如果有的话）。
• body的首个字符为非终结符，递归求解该非终结符first集，记为temp，同时将空串标记记为false，将temp的中除空串外的字符加入first集；若temp中有空串，记空串标记为true，继续遍历当前body的字符，理解上可以将body后面的字符串视为一个新的body继续进行求解步骤。
• body的字符遍历结束后若空串标记hasBlank仍然为true，则将空串加入first集。
• 优化：递归求解的中间结果可以放在全局哈希First（或者换个名字避免冲突）中，避免重复的迭代（本代码没实现，下次一定）。

代码

/**
 * @brief Function for generating set of First(a)
 * @author 立秋小猪
 * @time: 2021/10/13
 * @notice: 要求产生体句型不得有空格
 *          左递归的产生体中必须有空串（必须能够终结）
 *          char \'#\' act as varepsilon 
 * **/

#include <iostream>
#include <unordered_map>
#include <vector>
#include <string>
#include <fstream>
#include <unordered_set>

using namespace std;

unordered_map<string, vector<string>> P; //产生式P的集合

void scan(){
    //scan函数实现从文件扫描文法，将对应的产生式加入到映射P中
    fstream fs;
    string input;
    fs.open("lan.txt");
    if(!fs.is_open()){ // 文件打开失败
        cout << "Error: Could not open the file" << endl;
        exit(-1);
    }
    fs >> input;
    while(input != "end"){
        string VN = input; // 产生式的非终结符

        fs >> input; //跳过推导符号
        if (input != "->" && input != "→"){
            cout << "Error: undefined symbol [" << input << "]" << endl;
            exit(-2);
        }

        fs >> input; //产生体拆开后加入到set集合中，默认推导符号后必有一个产生体
        P[VN].emplace_back(input);
        while( fs >> input && input == "|"){
                fs >> input;
                P[VN].emplace_back(input);
        }
    }
}

// void generate(){
// }

unordered_set<char> First(const string& str){
    // 终结符以及空串情况下, whether has the VN or not
    if(str == "" || str == "#" || P.find(str) == P.end())
        return {};
    if(!(str[0] >= \'A\' && str[0] <= \'Z\'))
        return {str[0]};

    vector<string> bodys = P[str]; // str -> bodys
    unordered_set<char> res = {};
    for(auto &s: bodys){
        bool hasBlank = true;//是否含有空串，是否继续读产生体
        for (int i = 0; i < s.size() && hasBlank; ++i){
            if(s[i] >= \'A\' && s[i] <= \'Z\'){//是否为终结符
                unordered_set<char> temp = {};//递归的临时集
                string next;
                if(i < s.size() - 1 && s[i + 1] == \'\\\'\'){ // 大写字母 + \' 的非终结符
                    next = s.substr(i, 2);
                    ++i;
                }else{ //仅仅是大写字母的终结符
                    next = s[i];
                }
                if(next != str){ //避免无限递归，默认自身是含有空串（hasBlank为True）
                    temp = First(next); //递归求解
                    hasBlank = false; //先默认temp中没有空串
                    for(auto &c : temp)
                        if(c == \'#\')
                            hasBlank = true;//temp中发现了空串
                        else
                            res.emplace(c);
                }
            }else{
                res.emplace(s[i]);
                hasBlank = false;//默认连接的终结符不为空，故此终结符后不会再有新元素加入First集
            }
        }
        if(hasBlank) //产生体中所有非终结符都包含空串，则将空串加入first集中
            res.emplace(\'#\');
    }
    return res;
}



int main(){
    // unordered_map<string, vector<char>> First; //First集合
    scan();
    cout << "输入的产生式如下：\\n"
         << "********************************\\n";
    for(auto &[vn, bodys]: P){
        cout << vn << " -> " << bodys[0];
        for (int i = 1; i < bodys.size(); ++i)
            cout << " | " << bodys[i];
        cout << endl;
    }
    cout << "********************************\\n";

    for(auto &[vn,_]: P){
        unordered_set<char> f = First(vn);
        cout << "First(" << vn << ") : ";
        auto iter = f.begin();

        if(iter != f.end()){
            cout << *iter;
            while(++iter != f.end()){
                cout << " , " << *iter;
            }
        }
        cout << endl;
    }

    return 0;
}

lan.txt文件内容

E -> TE\'
E\' -> +TE\' | #
T -> FT\'
T\' -> *FT\' | #
F -> (E) | id
end

运行结果

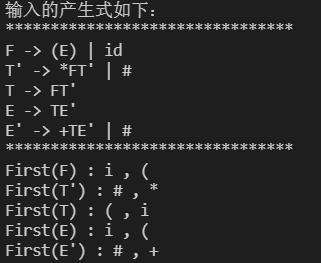
lan.txt文件内容

S -> SaRb | #
R -> RSQ | #
Q -> e
end

运行结果

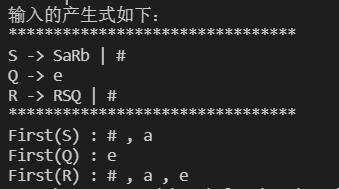
本人也只是编程小白，代码仅供参考，如有错误请见谅，如有疑问欢迎交流讨论，欢迎提出任何建议和评价。

编译原理：LL文法 语法分析器（预测分析表法）

设计要求：对于任意输入的一个LL(1)文法，构造其预测分析表，并对指定输入串分析其是否为该文法的句子。

思路：首先实现集合FIRST(X)构造算法和集合FOLLOW(A)构造算法，再根据FIRST和FOLLOW集合构造出预测分析表，并对指定的句子打印出分析栈的分析过程，判断是否为该文法的句子。

指定文法：

//文法
E->TK
K->+TK
K->$
T->FM
M->*FM
M->$
F->i
F->(E)

对于输入串i+i*i# ,这里我们先给出实验结果截图：

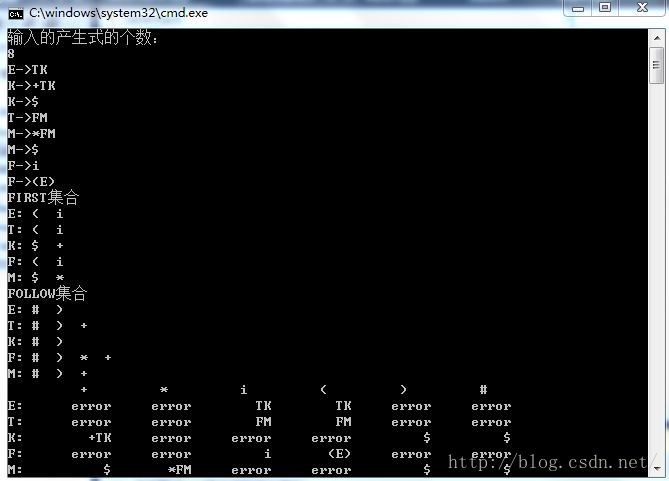
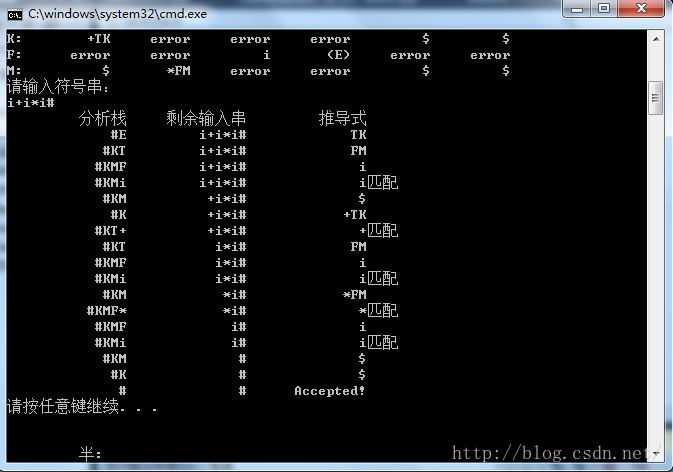
这个实验花了我一天的时间，主要难点在于first集和follow集中的递归判断部分，其他的只要按照下面的判断流程走就可以了。

（1）求FIRST集的算法思想

如果产生式右部第一个字符为终结符，则将其计入左部first集
 如果产生式右部第一个字符为非终结符
 ->求该非终结符的first集
 ->将该非终结符的非$first集计入左部的first集
->若存在$，则将指向产生式的指针右移
->若不存在$，则停止遍历该产生式，进入下一个产生式
->若已经到达产生式的最右部的非终结符，则将$加入左部的first集
 处理数组中重复的first集中的终结符

（2）求FOLLOW集的算法思想

 对于文法G中每个非终结符A构造FOLLOW(A)的办法是,连续使用下面的规则,直到每个FOLLOW不在增大为止.
(1) 对于文法的开始符号S,置#于FOLLOW(S)中;
(2) 若A->aBb是一个产生式,则把FIRST(b)\\{ε}加至FOLLOW(B)中;
(3) 若A->aB是一个产生式,或A->aBb是一个产生式而b=>ε(即ε∈FIRST(b))则把FOLLOW(A)加至FOLLOW(B)中

（3）生成预测分析表的算法思想

构造分析表M的算法是： 
 (1) 对文法G的每个产生式A->a执行第二步和第三步;
 (2) 对每个终结符a∈FIRST(a),把A->a加至M[A,a]中;
 (3) 若ε∈FIRST(a),则把任何b∈FOLLOW(A)把A->a加至M[A,b]中;
 (4) 把所有无定义的M[A,a]标上出错标志.

（4）对符号串的分析过程

 预测分析程序的总控程序在任何时候都是按STACK栈顶符号X和当前的输入符号行事的,对于任何(X,a),总控程序
 每次都执行下述三种可能的动作之一;
(1) 若X=a=”#”,则宣布分析成功,停止分析过程.
(2) 若X=a≠”#”,则把X从STACK栈顶逐出,让a指向下一个输入符号.
(3) 若X是一个非终结符,则查看分析表M,若M[A,a]中存放着关于X的一个产生式,那么,首先把X逐出STACK栈顶,然后
把产生式的右部符号串按反序一一推进STACK栈(若右部符号为ε,则意味着不推什么东西进栈).在把产生式的右部
符号推进栈的同时应做这个产生式相应得语义动作,若M[A,a]中存放着”出错标志”,则调用出错诊察程序ERROR.
 

在我的程序中，Base类为基类，负责求出FIRST和FOLLOW集；TableStack继承Base类，求出预测分析表和显示符号串的分析过程。

Base.h

struct node
{
	char left;
	string right;
};

class Base
{
protected:
	int T;
	node analy_str[100]; //输入文法解析

	set<char> first_set[100];//first集
	set<char> follow_set[100];//follow集
	vector<char> ter_copy; //去$终结符
	vector<char> ter_colt;//终结符
	vector<char> non_colt;//非终结符

public:
	Base() :T(0){}
	bool isNotSymbol(char c);
	int get_index(char target);//获得在终结符集合中的下标
	int get_nindex(char target);//获得在非终结符集合中的下标
	void get_first(char target); //得到first集合
	void get_follow(char target);//得到follow集合
	void inputAndSolve(); //处理得到first和follow
	void display(); //显示

};

TableStack.h

class TableStack :public Base
{
protected:
	vector<char> to_any; //分析栈
	vector<char> left_any;//剩余输入串
	int tableMap[100][100];//预测表
public:
	TableStack(){ memset(tableMap, -1, sizeof(tableMap)); }

	void get_table(); //得到预测表
	void analyExp(string s); //分析栈的处理
	void print_out();//输出
	void getAns(); //结合处理
};

接下来只列出FIRST集中的核心递归过程，有详细注释：

void Base::get_first(char target)
{
	int tag = 0;
	int flag = 0;
	for (int i = 0; i<T; i++)
	{
		if (analy_str[i].left == target)//匹配产生式左部
		{
			if (!isNotSymbol(analy_str[i].right[0]))//对于终结符，直接加入first
			{
				first_set[get_index(target)].insert(analy_str[i].right[0]);
			}
			else
			{
				for (int j = 0; j<analy_str[i].right.length(); j++)
				{
					if (!isNotSymbol(analy_str[i].right[j]))//终结符结束
					{
						first_set[get_index(target)].insert(analy_str[i].right[j]);
						break;
					}
					get_first(analy_str[i].right[j]);//递归
					//	cout<<"curr :"<<analy_str[i].right[j];
					set<char>::iterator it; 
					for (it = first_set[get_index(analy_str[i].right[j])].begin(); it != first_set[get_index(analy_str[i].right[j])].end(); it++)
					{
						if (*it == '$')
							flag = 1;
						else
							first_set[get_index(target)].insert(*it);//将FIRST(Y)中的非$就加入FIRST(X)
					}
					if (flag == 0)
						break;
					else
					{
						tag += flag;
						flag = 0;
					}
				}
				if (tag == analy_str[i].right.length())//所有右部first(Y)都有$,将$加入FIRST(X)中
					first_set[get_index(target)].insert('$');
			}
		}
	}

}

这个语法分析的全部工程代码在我的

Github

上，欢迎大家star学习，希望可以给大家带来帮助。