OpenCV——直方图

Posted 2021-04-03 Arthur的仓库

一、直方图概述

在统计学中，直方图是一种对数据分布情况的图形表示，是一种二维统计图表，他的两个坐标分别是统计样本（图像、视频帧）和样本的某种属性（亮度，像素值，梯度，方向，色彩等等任何特征）。

也可以这么理解，直方图是对数据的统计，并把统计值显示到事先设定好的bin（矩形条）中，bin中的数值是从数据中计算出的特征的统计量。总之，直方图获取的是数据分布的统计图，通常直方图的维数要低于原始数据。

图像直方图是用一表示数字图像中亮度分布的直方图，标绘了图像中每个亮度值的像素数。可以借助观察该直方图了解需要如何调整亮度分布的直方图。这种直方图中，横坐标的左侧为纯黑、较暗的区域，而右侧为较亮、纯白的区域。因此，一张较暗图片的图像直方图中的数据多集中于左侧和中间部分，而整体明亮、只有少量阴影的图像则相反。计算机视觉邻域常借助图像直方图来实现图像的二值化。

灰度直方图是一幅图像中个像素灰度值出现次数或频数的统计结果，它只反映该图像中灰度值出现的频率，而未反映某一灰度值像素所在的位置。也就是说，它只包含了该图像中某个灰度值的像素出现的概率，而丢失了其所在的位置的信息。任一幅图像，都能唯一地算出一幅与它对应的直方图。但不同的图像，可能有相同的直方图。即图像与直方图之间是多对一的映射关系。

直方图意义：

1.直方图是图像中像素强度分布的图形表达方式。

2.直方图统计了每一个强度值所具有的像素个数。

直方图术语：

dims：需要统计的特征的数目。例如：dims=1，表示我们仅统计灰度值。

bins：每个特征空间子区段的数目。

range：每个特征空间的取值范围。

二、直方图均衡化

直方图均衡化是通过拉伸像素强度的分布范围，使得在0~255灰阶上的分布更加均衡，提高了图像的对比度，达到改善图像主观视觉效果的目的。对比度较低的图像适合使用直方图均衡化方法来增强图像细节。

函数原型：

参数：

src：源图像，需为8位单通道图像

dst：输出图像，尺寸、类型和源图像一致

该函数采用如下步骤对输入图像进行直方图均衡化：

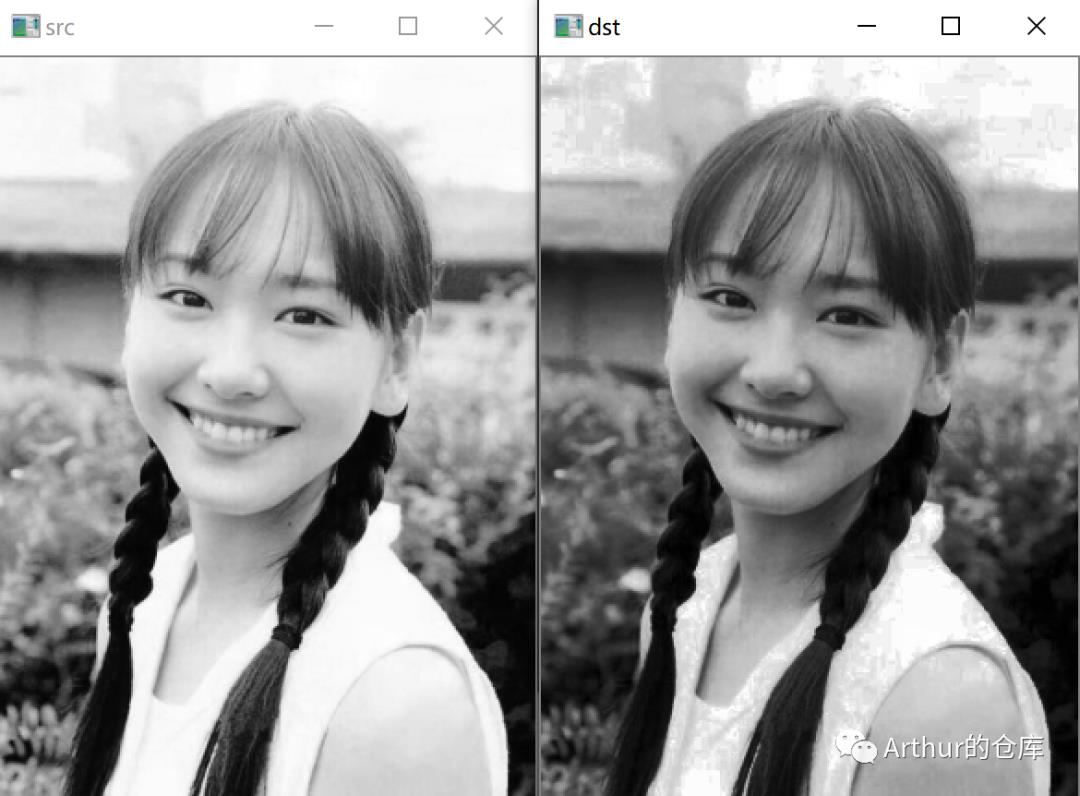
效果：

#define HIST_SIZE 256//计算直方图数据的函数static Mat cal_histogram(const Mat& src){ int hist[HIST_SIZE] = {0}; //遍历图像，对直方图对应的格子累加计算 for (int i = 0; i < src.rows; i++) { for (int j = 0; j < src.cols; j++) { int idx = src.ptr<uchar>(i)[j]; if (idx < HIST_SIZE) { hist[idx]++; } } } //把直方图数据从数组转换成只有一列的矩阵 Mat histMat(HIST_SIZE, 1, CV_32FC1); for (int i = 0; i < HIST_SIZE; i++) { histMat.ptr<float>(i)[0] = hist[i]; } return histMat;}//定义函数把直方图以图像形式显示static void show_histogram(const Mat& src, String winName){ //先调用计算直方图的函数得到直方图数据，并归一化到0-255 Mat hist = cal_histogram(src); normalize(hist, hist, 0, 255, NORM_MINMAX, CV_8UC1); //定义用于显示的图像 Mat hist2 = Mat(300, 256, CV_8UC1, Scalar(0)); //遍历直方图，一个格子的数据画一条竖线 for (int i = 0; i < HIST_SIZE; i++) { //从左到右，高度相反画图线 line(hist2, Point(i, 299), Point(i, 299 - hist.at<uchar>(i)), Scalar(255), 1, LINE_AA); } imshow(winName, hist2);}

均衡化前后强度对比：

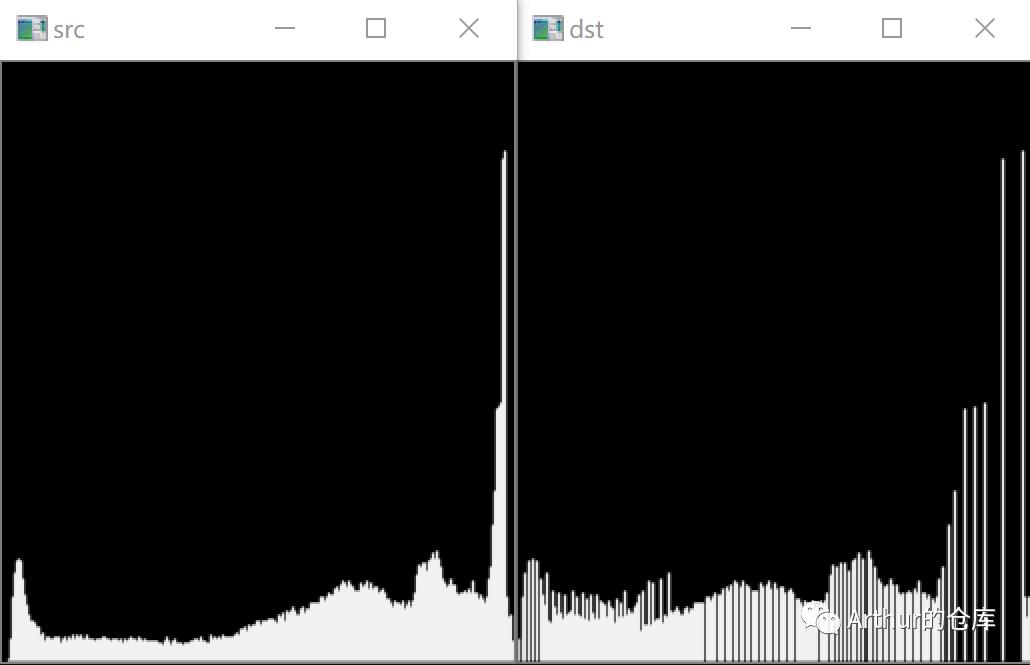
均衡化前，像素强度分布相对集中，均衡化后，分布相对散开一点，对比度就改善了。

如果图像是彩色图像，则先分离通道，分别做均衡化，再合并通道。

vector<Mat>channels;split(src, channels);Mat blue, green, red;blue = channels.at(0);green = channels.at(1);red = channels.at(2);equalizeHist(blue, blue);equalizeHist(green, green);equalizeHist(red, red);merge(channels, dst);

效果：

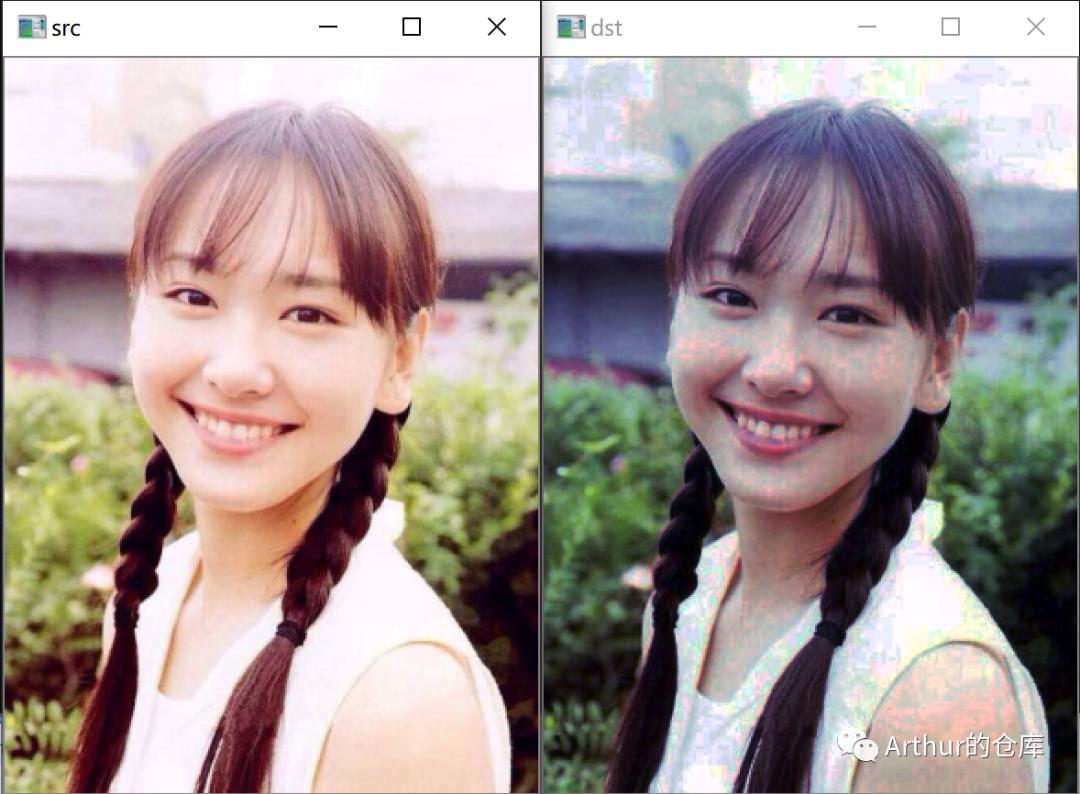
具体实现：

static Mat histogram_equalize(Mat& src){ //第一步，计算直方图数据 Mat hist = cal_histogram(src); //第二步，计算累积直方图，同时进行第三步，把累积直方图的数据归一化到0-255 int hist_accumulate[HIST_SIZE]; int sum = 0; int total_number_pixels = src.cols * src.rows; for (int i = 0; i < HIST_SIZE; i++) { sum += (int)hist.ptr<float>(i)[0]; hist_accumulate[i] = saturate_cast<uchar>(sum * 255 / total_number_pixels); } //第四步，遍历原图像，以原图像的像素值为索引，从第三步的归一化后的直方图中取值组成最终均衡化图像 Mat dst(src.size(), CV_8UC1); for (int i = 0; i < dst.rows; i++) { for (int j = 0; j < dst.cols; j++) { dst.ptr<uchar>(i)[j] = hist_accumulate[src.ptr(i)[j]]; } } return dst;}

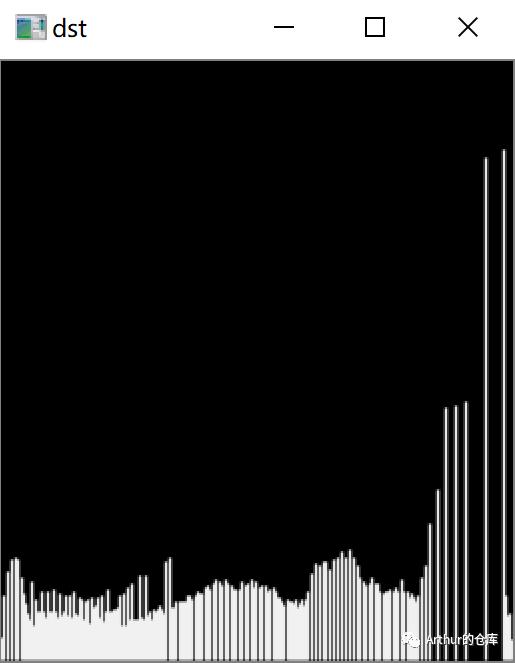
效果：

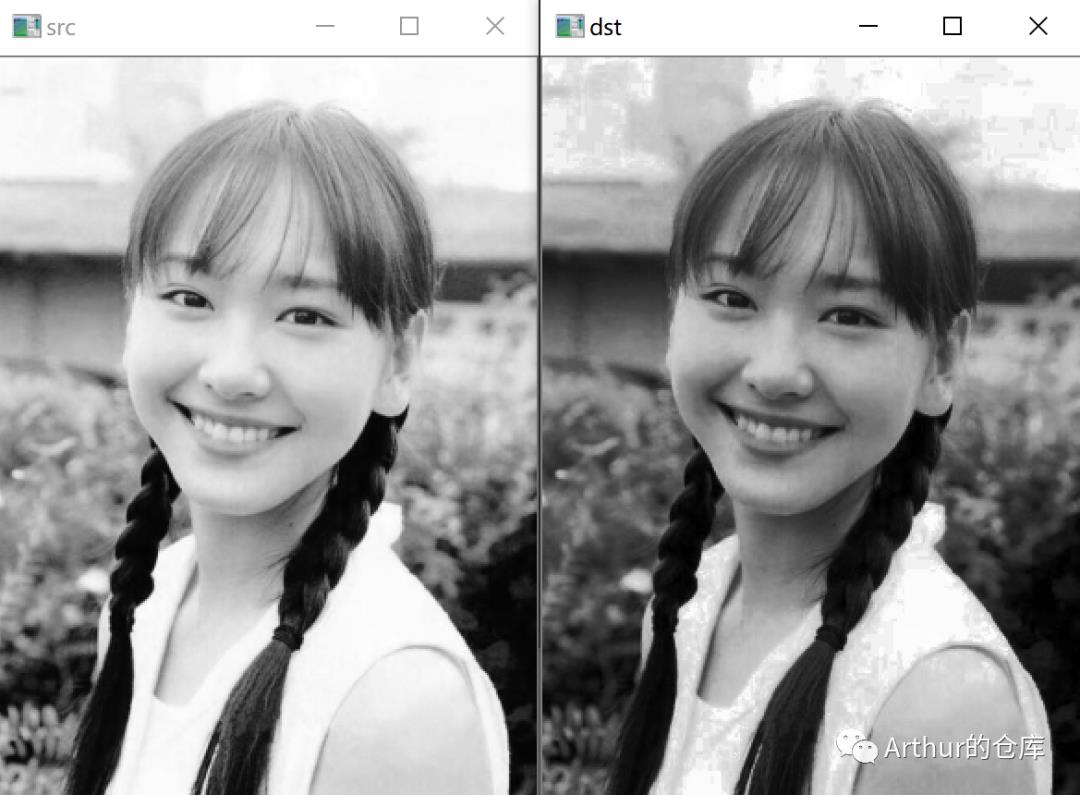
可以看出和opencv的效果有些不同，opencv在计算归一化因子时，是255 / (总计数 - 第一个非零计数)，累积直方图时，第一个非零计算及之前的，累积都为0。

三、直方图的计算与绘制

函数原型：

参数：

images：用于计算直方图的图像矩阵，可以是多个图像

nimages：指明有多少输入图像要计算直方图

channels：指明用于计算的图像通道，第一张图，通道值为0到images[0].channels - 1，第二张图，通道值为images[0].channels到images[0].channels + images[1].channels - 1，以此类推

mask：掩码矩阵，如指定，对应的非零像素值才参与计算（其中把需要处理的部分指定为1，不需要处理的部分指定为0，一般设置为None，表示处理整幅图像）

hist：输出的直方图数据

dims：直方图的维数，一般以一维和二维用的比较多

histSize：直方图数据每一维的大小，即每一维多少份，或者说使用多少个直方柱（bin），一般为256

ranges：直方图数据每一维数据的范围，如果uniform为true的话，每一维只需给定范围的最大值（不包含）和最小值（包含），然后会自动按histSize给定的对应维的大小平均计算每一份的分界值；如果uniform为false，那么每一维要按histSize对应的大小给出每一份的分界值，即每一维要按histSize对应的大小给出每一份的分界值，即每一维都要由对应histSize的大小+1值来指定

uniform：参考ranges，也就是说每个竖条的宽度是否相等

accumulate：如果为true，则每一组数据的直方图数据会进行累加，否则不会累加

//定义各个参数值 //只有一张图像int nimages = 1;//对哪个通道进行计算int channels[] = { 0 };//掩码矩阵，这里数据是空的，即不使用掩码Mat mask = Mat();//一维直方图int dims = 1;//只有一维，此维度的尺寸为256，即像素的取值为0到255int histSize[] = { 256 };//此维的取值范围为0到255float histRange[] = { 0,256 };//定义为函数能接受的类型，即常量指针的指针const float* ranges[] = { histRange };//均匀取值，不累加bool uniform = true;bool accumulate = false;
//调用opencv的calcHist，BGR三个通道分别计算Mat hist_b, hist_g, hist_r;calcHist(&src, nimages, channels, mask, hist_b, dims, histSize, ranges, uniform, accumulate);channels[0] = 1;calcHist(&src, nimages, channels, mask, hist_g, dims, histSize, ranges, uniform, accumulate);channels[0] = 2;calcHist(&src, nimages, channels, mask, hist_r, dims, histSize, ranges, uniform, accumulate);
//定义一个新的图像，用于输出三个通道对应的直方图曲线//定义宽高，宽为512，即256的2倍，对于8位的灰度图，即为每个像素值对应0到512中连续两个数int width = 512, height = 500;int binWidth = cvRound((double)width / histSize[0]);Mat hist = Mat(height, width, CV_8UC3, Scalar(0));//把直方图归一化，从0到新图像的高度，即0到500normalize(hist_b, hist_b, 0, height, NORM_MINMAX, CV_32FC1);normalize(hist_g, hist_g, 0, height, NORM_MINMAX, CV_32FC1);normalize(hist_r, hist_r, 0, height, NORM_MINMAX, CV_32FC1);//从0开始，把相邻两个值画线，x方向乘以每一份的宽度，y方向把方向倒一下，三个通道的数据用不同的颜色for (int i = 1; i < histSize[0]; i++){ line(hist, Point(binWidth * (i - 1), height - cvRound(hist_b.at<float>(i - 1))), Point(binWidth * (i), height - cvRound(hist_b.at<float>(i))), Scalar(255, 0, 0), 2, LINE_AA, 0); line(hist, Point(binWidth * (i - 1), height - cvRound(hist_g.at<float>(i - 1))), Point(binWidth * (i), height - cvRound(hist_g.at<float>(i))), Scalar(0, 255, 0), 2, LINE_AA, 0); line(hist, Point(binWidth * (i - 1), height - cvRound(hist_r.at<float>(i - 1))), Point(binWidth * (i), height - cvRound(hist_r.at<float>(i))), Scalar(0, 0, 255), 2, LINE_AA, 0);}
//上面是画直线，这里画柱状//把三个通道的直方图数据再归一化到0 - 255，即8位图的取值范围normalize(hist_b, hist_b, 0, 255, NORM_MINMAX, CV_8UC1);normalize(hist_g, hist_g, 0, 255, NORM_MINMAX, CV_8UC1);normalize(hist_r, hist_r, 0, 255, NORM_MINMAX, CV_8UC1);//定义新图用于画柱状图Mat hist2 = Mat(300, 256, CV_8UC3, Scalar(0));//每个像素值对应一格，按值的大小，画一根垂直线for (int i = 0; i < histSize[0]; i++){ line(hist2, Point(i, 299 - hist_b.at<uchar>(i)), Point(i, 299), Scalar(255, 0, 0), 2, LINE_AA, 0); line(hist2, Point(i, 299 - hist_g.at<uchar>(i)), Point(i, 299), Scalar(0, 255, 0), 2, LINE_AA, 0); line(hist2, Point(i, 299 - hist_r.at<uchar>(i)), Point(i, 299), Scalar(0, 0, 255), 2, LINE_AA, 0);}

效果：

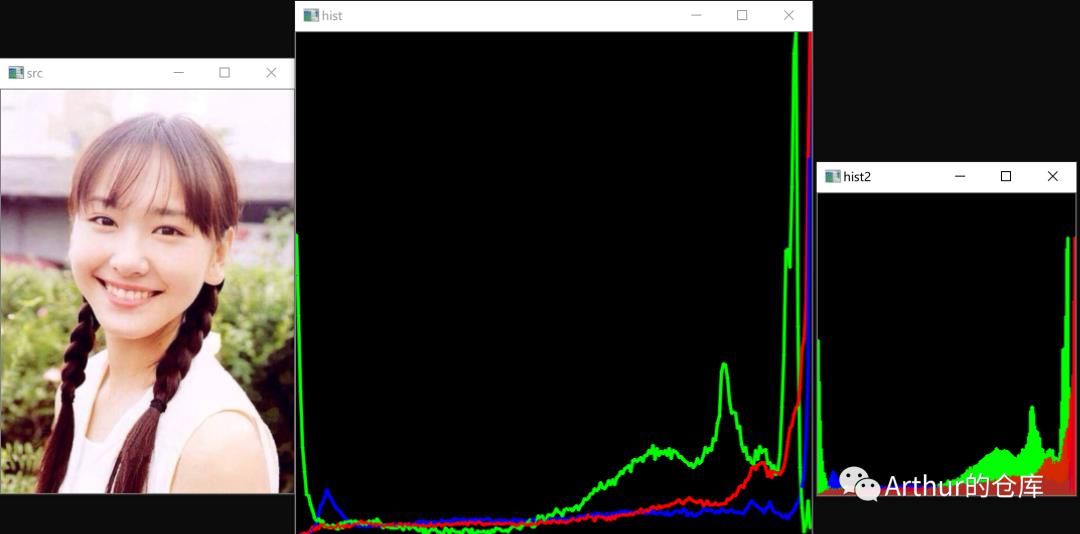
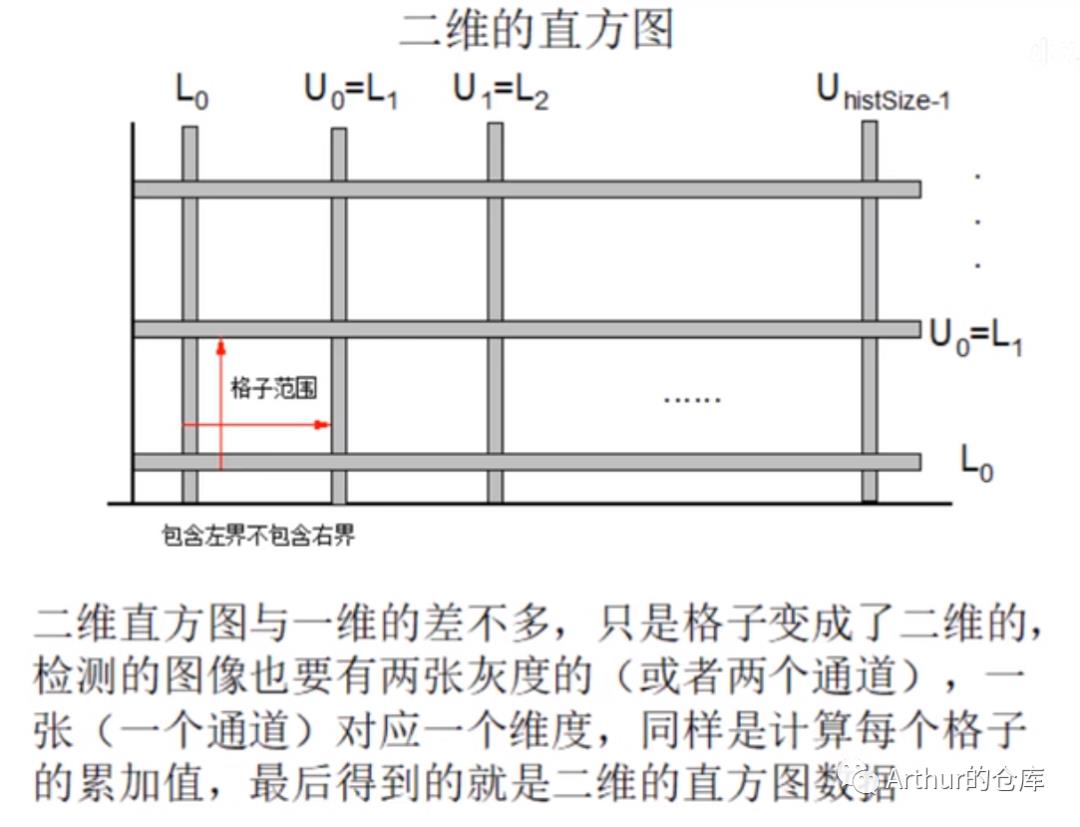
二维直方图：

Mat hsv;//转换为HSV色彩模型cvtColor(src, hsv, COLOR_BGR2HSV);//定义色度和饱和度这两维的大小，即分多少份int hbins = 30, sbins = 32;int hsHistSize[] = { hbins, sbins };//色度和饱和度的范围float hranges[] = { 0,180 };float sranges[] = { 0, 256 };const float* hsranges[] = { hranges, sranges };//使用0，1两个通道来计算Mat hist;int hschannels[] = { 0, 1 };int nimages = 1;int dims = 2;Mat mask = Mat();bool uniform = true;bool accumulate = false;//调用opencv函数calcHist(&hsv, nimages, hschannels, mask, hist, dims, hsHistSize, hsranges, uniform, accumulate);//归一化到8位图的数值范围normalize(hist, hist, 0, 255, NORM_MINMAX, CV_8UC1);//新建图像用于显示直方图的值，宽高大小为这两维大小的10倍int scale = 10;Mat hist_scale = Mat::zeros(hist.rows * scale, hist.cols * scale, CV_8UC1);for (int i = 0; i < hbins; i++){ for (int j = 0; j < sbins; j++) { //取直方图每一格的数据，然后在新图像相应长宽都放大10倍的格子（矩形）填上直方图的值 rectangle(hist_scale, Rect(Point(j * scale, i * scale), Point((j + 1) * scale - 1, (i + 1) * scale - 1)), Scalar(hist.ptr<uchar>(i)[j]), FILLED); }}

效果：

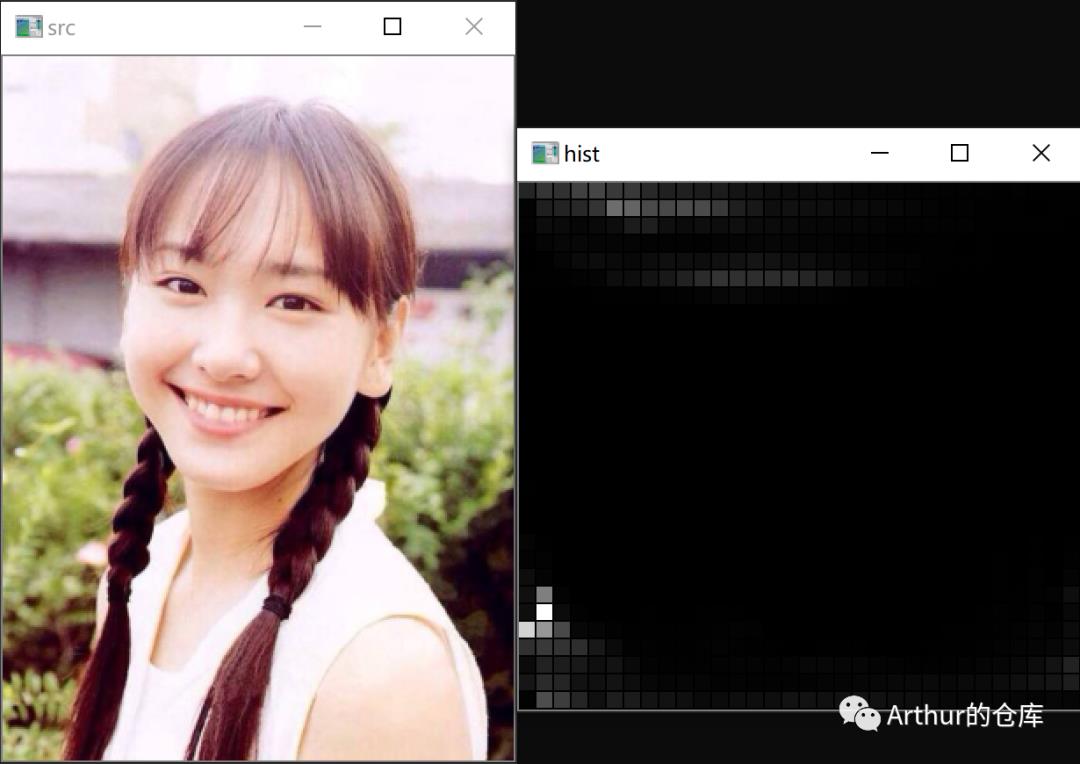
直方图计算实现：

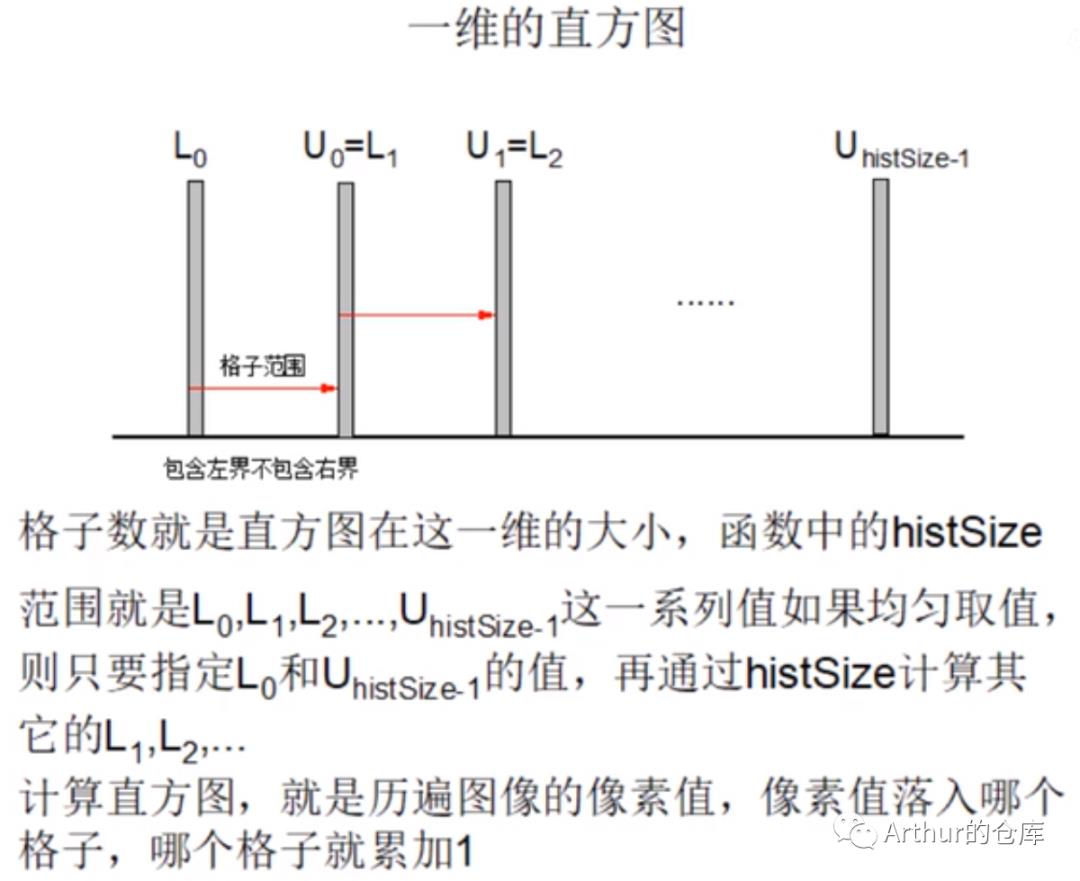
static Mat my_cal_hist(const Mat& src, int* channels, int dims, int* histSize, const float** ranges){ Mat hist; if (dims == 1) { //尺寸，即有几个格子 int hs = histSize[0]; //范围，即格子开始与结束的值 const float* ranges1 = ranges[0]; float start = ranges1[0], end = ranges1[1]; //采取均匀的方法，因此每个格子的大小确定 float step = (end - start) / (float)hs; //直方图为一个列向量，初始化直方图数据为0 hist = Mat::zeros(hs, 1, CV_32FC1); //如果原图有多个通道，取出要用来计算的那个通道 Mat mat = src; if (src.channels() > 1) { vector<Mat> mats; split(src, mats); mat = mats[channels[0]]; } //遍历图像，看像素值落入哪个格子，相应格子计数加1 for (int i = 0; i < mat.rows; i++) { for (int j = 0; j < mat.cols; j++) { //像数值 float value = (float)mat.ptr<uchar>(i)[j]; //格子索引值 int idx = 0; //查找像素落入的那个格子 for (float f = start; f < end; f += step) { //如果这个像素找到合适格子，退出进行下一个像素的处理 if (value >= f && value < f + step) { hist.ptr<float>(idx)[0]++; break; } //如果不符合，格子索引加1，进入下一个格子的检测 idx++; } } } } else if (dims == 2) { //尺寸，即再两个维度分别分几份 int s1 = histSize[0], s2 = histSize[1]; //两个维度各自的范围 const float* ranges1 = ranges[0]; const float* ranges2 = ranges[1]; float start1 = ranges1[0], end1 = ranges1[1]; float start2 = ranges2[0], end2 = ranges2[1]; //采用均匀分割范围，两个维度分割大小要计算出来 float step1 = (end1 - start1) / (float)s1; float step2 = (end2 - start2) / (float)s2; //初始化二维直方图数据为0 hist = Mat::zeros(s1, s2, CV_32FC1); //取出用于计算直方图的两个通道 Mat mat1, mat2; vector<Mat> mats; split(src, mats); mat1 = mats[channels[0]]; mat2 = mats[channels[1]]; //开始遍历两个通道，即两个矩阵 for (int i = 0; i < mat1.rows; i++) { for (int j = 0; j < mat2.cols; j++) { //取出用于第一维的像素值 float value1 = (float)mat1.ptr<uchar>(i)[j]; //第一维的格子索引 int idx1 = 0; //遍历第一维的格子 for (float f1 = start1; f1 < end1; f1 += step1) { //如果第一维的位置找到的话 if (value1 >= f1 && value1 < f1 + step1) { //取第二维的像素值 float value2 = (float)mat2.ptr<uchar>(i)[j]; //格子第二维的索引 int idx2 = 0; //遍历格子第二维的位置 for (int f2 = start2; f2 < end2; f2 += step2) { if (value2 >= f2 && value2 < f2 + step2) { //第二维的位置找到的话，直方图对应格子计数加1，并退出第二维的遍历 hist.ptr<float>(idx1)[idx2] += 1; break; } //第二维的位置未找到，索引加1，即进行第二维下一位置的检测 idx2++; } //第一维的位置找到，前面第二维的位置也找到，因此此像素处理完 break; } //当前第一维位置不符合要求，找第一维的下一个位置 idx1++; } } } } return hist;}

四、直方图比较

直方图比较，是用一定的标准来判断两个直方图的相似度方法

对输入的两张图像计算得到直方图H1与H2，归一化到相同的尺度空间然后可以通过计算H1与H2的之间的距离得到两个直方图的相似程度进而比较图像本身的相似程度。

Opencv提供的比较方法有四种：Correlation 相关性比较

Chi - Square 卡方比较

Intersection 十字交叉性

Bhattacharyya distance 巴氏距离

步骤：首先把图像从RGB色彩空间转换到HSV色彩空间cvtColor

计算图像的直方图，然后归一化到[0~1]之间calcHist和normalize

使用上述四种比较方法之一进行比较compareHist

函数原型：

注意：相关系数越接近1越相似，卡方检验值越小越相似

//读入两张相似的图像Mat src1 = imread("src1.png");Mat src2 = imread("src2.png");if (src1.empty() || src2.empty()){ cout << "图片打开失败"; return -1;}//步骤一：从RGB空间转换到HSV空间Mat hsv1, hsv2;cvtColor(src1, hsv1, CV_RGB2HSV);cvtColor(src2, hsv2, CV_RGB2HSV);//步骤二：分别计算两张图像的直方图并归一化int hbins = 30, sbins = 32;int hsHistSize[] = { hbins, sbins };float hranges[] = { 0,180 };float sranges[] = { 0, 256 };const float* hsranges[] = { hranges, sranges };Mat hist;int hschannels[] = { 0, 1 };int nimages = 1;int dims = 2;Mat mask = Mat();bool uniform = true;bool accumulate = false;MatND hist1, hist2;calcHist(&hsv1, nimages, hschannels, mask, hist1, dims, hsHistSize, hsranges, uniform, accumulate);calcHist(&hsv2, nimages, hschannels, mask, hist2, dims, hsHistSize, hsranges, uniform, accumulate);normalize(hist1, hist1, 0, 1, NORM_MINMAX, -1);normalize(hist2, hist2, 0, 1, NORM_MINMAX, -1);//步骤三：比较直方图，并返回值double d1 = compareHist(hist1, hist2, CV_COMP_CORREL);double d2 = compareHist(hist1, hist2, CV_COMP_CHISQR);double d3 = compareHist(hist1, hist2, CV_COMP_INTERSECT);double d4 = compareHist(hist1, hist2, CV_COMP_BHATTACHARYYA);

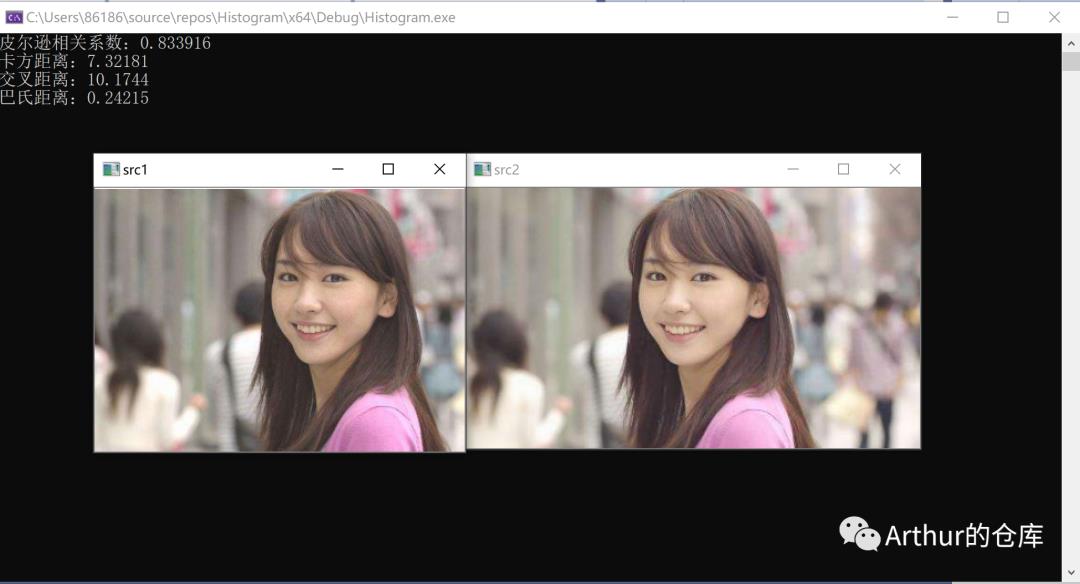
直方图比较实现

static double my_compareHist(const Mat& hist1, const Mat& hist2, int method){ int n = hist1.rows * hist1.cols; double s1 = 0, s2 = 0; //计算两个直方图数据总和 for (int i = 0; i < hist1.rows; i++) { for (int j = 0; j < hist1.cols; j++) { s1 += hist1.ptr<float>(i)[j]; s2 += hist2.ptr<float>(i)[j]; } } //计算平均值 double m1 = s1 / n; double m2 = s2 / n;
 double d; switch (method) { case CV_COMP_CORREL: { //计算公式中分子分母 double s11 = 0, s12 = 0, s22 = 0; for (int i = 0; i < hist1.rows; i++) { for (int j = 0; j < hist1.cols; j++) { double f1 = hist1.ptr<float>(i)[j]; double f2 = hist2.ptr<float>(i)[j]; s11 += (f1 - m1) * (f1 - m1); s12 += (f1 - m1) * (f2 - m2); s22 += (f2 - m2) * (f2 - m2); double s11xs22 = s11 * s22; //确保分母不能为0，否则相关系数要设为1 if (s11xs22 != 0) { d = s12 / sqrt(s11xs22); } else { d = 1; } } } break; } case CV_COMP_CHISQR: { d = 0; for (int i = 0; i < hist1.rows; i++) { for (int j = 0; j < hist1.cols; j++) { double f1 = hist1.ptr<float>(i)[j]; double f2 = hist2.ptr<float>(i)[j]; if (f1 != 0) { d += (f1 - f2) * (f1 - f2) / f1; } } } break; } case CV_COMP_INTERSECT: { d = 0; for (int i = 0; i < hist1.rows; i++) { for (int j = 0; j < hist1.cols; j++) { double f1 = hist1.ptr<float>(i)[j]; double f2 = hist2.ptr<float>(i)[j]; d += min(f1, f2); } } break; } case CV_COMP_BHATTACHARYYA: { double sqrt_s12 = 0; for (int i = 0; i < hist1.rows; i++) { for (int j = 0; j < hist1.cols; j++) { double f1 = hist1.ptr<float>(i)[j]; double f2 = hist2.ptr<float>(i)[j]; sqrt_s12 += sqrt(f1 * f2); } } d = sqrt(1 - (1 / sqrt(m1 * m2 * n * n)) * sqrt_s12); break; } } return d;}

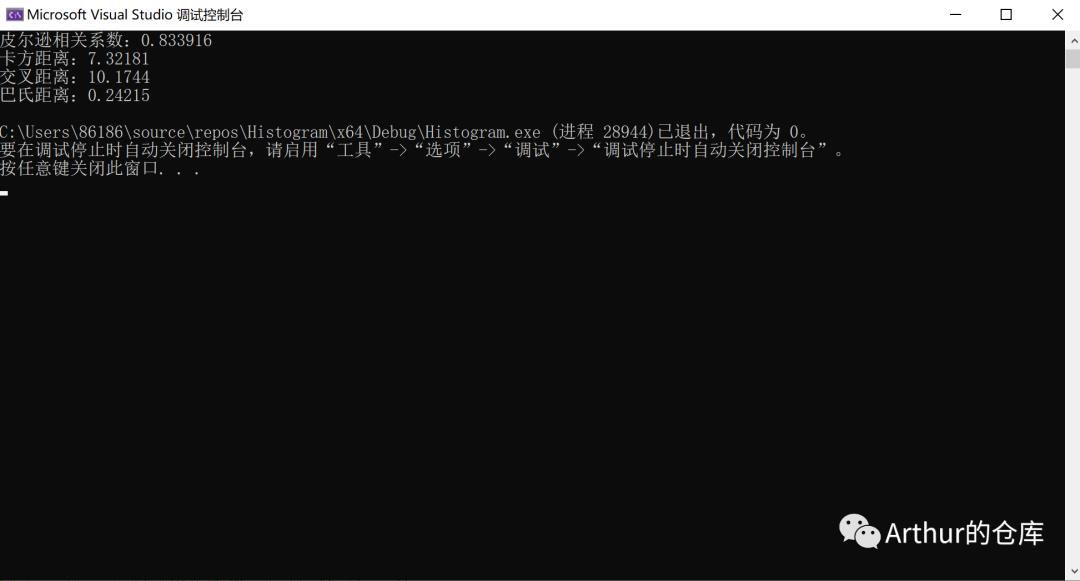
可以看到结果相同：

五、直方图的反向投影

反向投影是反映直方图模型在目标图像中的分布情况

简单点说就是用直方图模型去目标图像中寻找是否有相似的对象。通常用HSV色彩空间的HS两个通道直方图模型

步骤：

建立直方图模型

计算待测图像直方图并映射到模型中

从模型反向计算生成图像

原理：

取一个4*4大小的矩阵进行测试

//取一个4x4的矩阵Mat src = (Mat_<uchar>(4, 4) << 14, 13, 12, 12, 6, 8, 9, 4, 15, 2, 1, 3, 7, 5, 10, 3);cout << "Image=
" << src << endl;
//计算直方图int nimages = 1;int channels[] = { 0 };Mat mask = Mat();int dims = 1;int histSize[] = { 4 };float histRange[] = { 1,17 };const float* ranges[] = { histRange };bool uniform = true;bool accumulate = false;Mat hist;calcHist(&src, nimages, channels, mask, hist, dims, histSize, ranges, uniform, accumulate);cout << "Histogram=
" << hist << endl;
//反向投影Mat backProject;calcBackProject(&src, nimages, channels, hist, backProject, ranges);cout << "backProject=
" << backProject << endl;

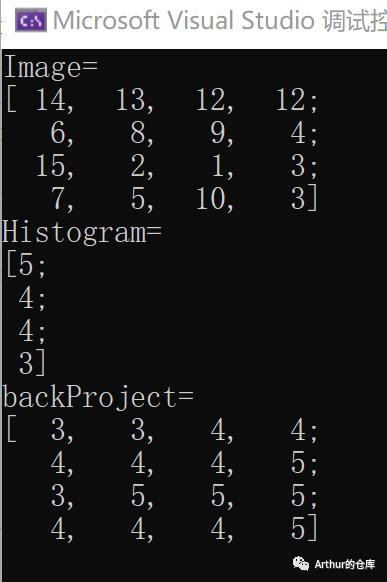
将Image的灰度等级分为4份，[1,5)，[5,9)，[9,13)，[13,17)，落入每个区间的像素个数为5，4，4，3，例如，14落入区间[13,17)，其区间内有3个像素，则反射投影位置3，依此类推

通过反射投影，实际上是原图像的256个灰度值被置为很少的几个值了，具体有几个值，要看把0~255划分为多少个区间。反向投影矩阵中某点的值就是它对应的原图像中的点所在区间的灰度直方图值。所以我们可以看出，一个区间点越多，在反向投影矩阵中就越亮。那么怎么理解反向投影矩阵中的“反向”二字呢？从这个过程可以看出，我们是先求出原图像的直方图，再由直方图得到反向投影矩阵，由直方图到反向投影矩阵实际上就是一个反向的过程，所以叫反向。通过图像的反向投影矩阵，我们实际上把原图像简单化了，简单化的过程实际上就是提取出图像的某个特征。所以以后我们可以用这个特征来对比两幅图，如果两幅图的反向投影矩阵相似或相同，那么我们就可以判定这两幅图这个特征是相同的

函数原型：

参数：

images：输入图像，图像深度必须位CV_8U, CV_16U或CV_32F中的一种，尺寸相同，每一幅图像都可以有任意的通道数

nimages：输入图像的数量

channels：用于计算反向投影的通道列表，通道数必须与直方图维度相匹配，第一个数组的通道是从0到image[0].channels() - 1，第二个数组通道从图像image[0].channels()到image[0].channels() + image[1].channels() - 1计数

hist：输入的直方图

backProject：目标反向投影输出图像，是一个单通道图像，与原图像有相同的尺寸和深度 

ranges：直方图中每个维度bin的取值范围

scale = 1：出反向投影的比例因子 

uniform = true：直方图是否均匀分布(uniform)

Mat hsv;//转换为HSV色彩模型cvtColor(src, hsv, CV_BGR2HSV);//创建一个图像Mat hue;hue.create(hsv.size(), hsv.depth());//从输入图像中拷贝某通道到输出图像中特定的通道int nchannels[] = { 0,0 };mixChannels(&hsv, 1, &hue, 1, nchannels, 1);//定义色度的大小int hbins = 6;int hHistSize[] = { hbins };//色度的范围float hranges[] = { 0,180 };const float* ranges[] = { hranges };
Mat hist;int hchannels[] = { 0 };int nimages = 1;int dims = 1;Mat mask = Mat();bool uniform = true;bool accumulate = false;//调用opencv函数calcHist(&hue, nimages, hchannels, mask, hist, dims, hHistSize, ranges, uniform, accumulate);//归一化到8位图的数值范围normalize(hist, hist, 0, 255, NORM_MINMAX, -1);//反向投影Mat backProject;calcBackProject(&hue, nimages, hchannels, hist, backProject, ranges, 1, true);

效果：

具体算法实现：

Mat my_calcBackProject(Mat& src, Mat& hist, float* ranges){ int n = hist.rows; float start = ranges[0]; float end = ranges[1]; float step = (end - start) / (float)n; Mat dst(src.size(), CV_8UC1); for (int i = 0; i < src.rows; i++) { for (int j = 0; j < src.cols; j++) { float value = (float)src.ptr<uchar>(i)[j]; int idx = 0; for (float k = start; k < end; k += step) { if (value >= k && value < k + step) { dst.ptr<uchar>(i)[j] = (uchar)hist.ptr<float>(idx)[0]; break; } idx++; } } } return dst;}