[概率论与数理统计]双盲试验随机数表法的应用转载

Posted 2021-10-11 千千寰宇

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了[概率论与数理统计]双盲试验随机数表法的应用转载相关的知识，希望对你有一定的参考价值。

在医学临床试验中可能经常使用到双盲试验、随机数表(抽样)法，遇到了便挤出时间了解一下、记一记。

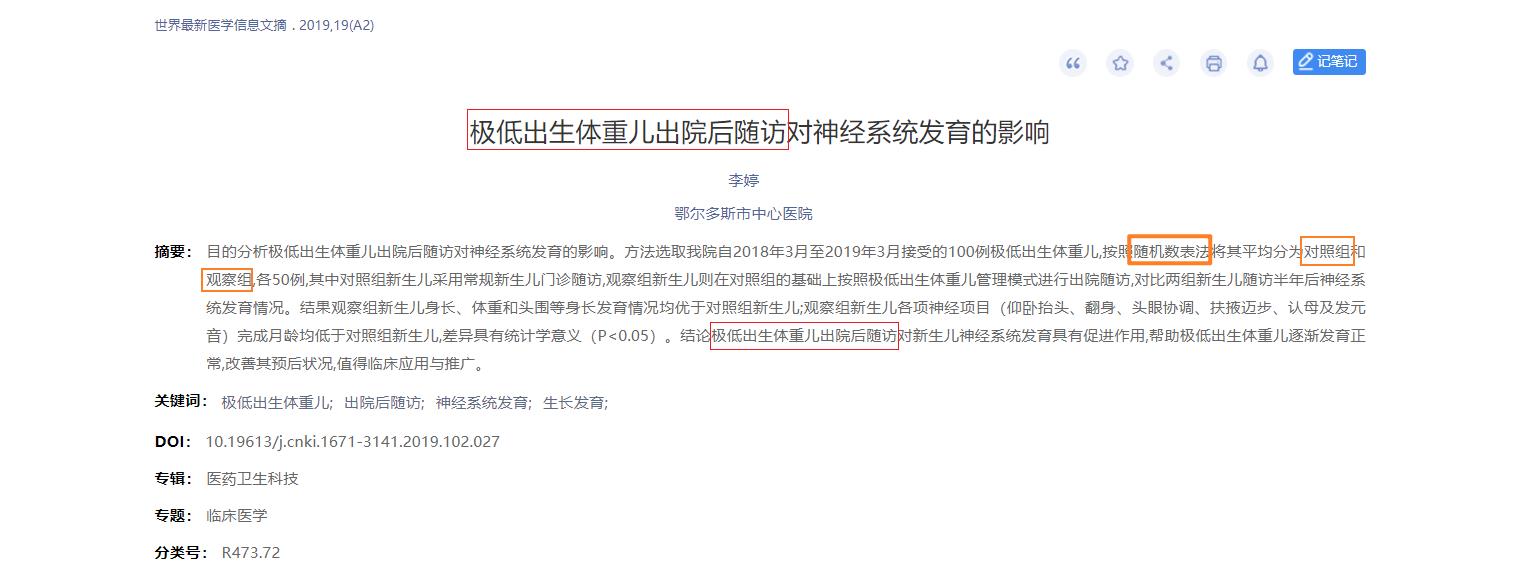
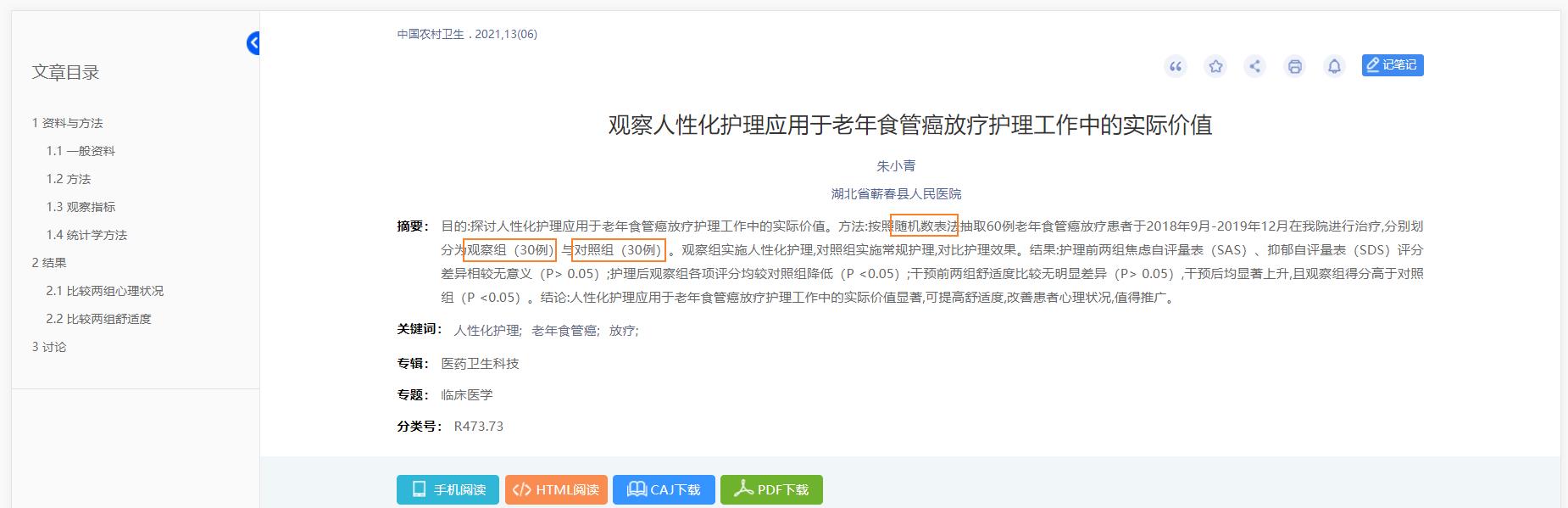
问题：有100个病患做为抽样样本，采用随机数表法，如何将其分成试验组（50人）和对照组(50人，安慰剂组)，步骤是怎样的？

双盲试验方法的优点: 双盲控制时让试验人员/研究人员和试验样本/受试对象都不知道实验的内容和目的，由于试验者和研究参加者都不知道哪些被试接受哪种试验条件，从而避免了主、被试双方因为主观期望所引发的额外变量

1.1 双盲试验

双盲试验，一种实验方法，是指在试验过程中：
1）测验者与被测验者都不知道被测者所属的组别（实验组或对照组）；
2）分析者在分析资料时，通常也不知道正在分析的样本资料属于哪一组；
旨在消除可能出现在实验者和参与者意识当中的主观偏差和个人偏好。
在大多数情况下，双盲实验要求达到非常高的科学严格程度。多应用在医学临床试验等领域。

1.2 盲的含义

盲在试验中是一种基本工具，用以在试验中排除参与者的有意识的或者下意识的个人偏爱。

比如，在非盲试验中检验受试者对不同品牌食品的偏爱，受试者往往选择他们偏爱的食品，但是在盲试验中，即品牌不能被辨认的情况下，受试者可以真正排除个人品牌偏好而进行试验。

最早意识到盲试验在科学研究中的的价值的人应该是克劳狄伯纳德( Claude Bernard)，他建议任何科学试验的参与者必须被分为两类:
(1)设计试验的理论家和
(2)没有相关知识，因此也不会在观测结果中添加个人对理论的理解的观测者。
这种对科学试验的认识与当时流行的启蒙时代的那种认为"科学观测只有由那些在受过良好教育的和对试验完全了解的科学家进行下才能产生可观的结果"的观点大相径庭。

这种试验方法用于:防止研究结果被安慰剂效应( placebo effect)或者观察者偏爱(observer bias)影响。
在试验中使一个人盲就是不告知他试验过程的信息。
按照使参与者盲的程度，这种试验被分为单盲(Single-blind)、双盲(double-blind)、三盲(triple-blind)试验。

1.3 盲的种类

1.3.1 单盲法: 参与样本不知情，但试验人员知情

单盲试验指的是这种试验：
在试验中可能引起个人偏好或者使试验结果发生偏差的信息不向试验的参与者（participant）提供，而试验的试验者（experimenter）却完全掌握关于试验的所有信息。
在单盲试验中，试验的参与者不知道他们是属于被试组/测试组（test subjects）还是属于试验控制组/对照组（experimental control groups)。

单盲试验一般以下这情况：
（1）试验者知道试验的全部信息，并且
（2）试验者不会在自己知道所有试验情况下对试验结果产生偏差，因此没有必要使试验者盲。
但是，可能的风险是试验的参与者在与观察者交流后受到他们的影响，即试验者自己的偏好被传递给了参与者造成试验的偏差。

单盲试验在心理学和社会科学研究中具有风险，因为试验者对结果的预期可能会有意识或者下意识地影响参与者而造成偏差。

1.3.2 双盲法: 参与样本不知情，且试验人员不知情【应用居多】

双盲试验是一种更加严格的试验方法，通常适用于以人为研究对象的试验（human subjects），旨在消除可能出现试验者和参与者意识当中的主观偏差（subjective bias）和个人偏好（personal preferences）。
在大多数情况下，双盲试验要求达到非常高的科学严格程度。

在双盲试验中，试验者和参与者都不知道哪些参与者属于对照组（control group）、哪些属于试验组（experimental group）。
只有在所有数据被记录完毕之后（在有些情况下是分析完毕之后），试验者才能知道那些参与者是哪些组的。
采用双盲试验是为了要减少偏见（prejudices）和无意识地暗示（unintentional physical cues）对试验结果的影响。
对于被试者的随机分配（Random assignment）到对照组或者试验组的做法是双盲试验中至关重要的一部。
确认哪些受试者属于那些组的信息交由第三方保管，并且在研究结束之前不能告知研究者。

1.3.3 三盲法：参与样本不知情，且试验人员不知情，且资料分析人员不知情

三盲法是双盲法的扩展，即: 受试对象、研究人员和资料分析人员均不知道受试对象的分组和处理情况。
这种方法在理论上可以减少资料分析上的偏差，但在分析时减弱了对整个研究工作的全局了解，对研究的安全性要求较高，在执行时也较严密，难度较大。

2 随机数表法————一种随机抽样方法

随机数表的应用领域：随机抽样、为顾客提供不同的ID、产品或商品的抽样检验、随机问卷对象的选择、抽奖活动等。

1.1 随机数表法、随机数表的关系与定义

随机号码表法/随机数表亦称“乱数表法”，就是在利用随机投掷骰子、或计算机模拟等方式生成的随机号码表抽取样本的【方法】。
随机号码表/随机数表又称为乱数表。

它是将0～9的10个自然数，按编码位数的要求（如两位一组，三位一组，五位甚至十位一组），利用特制的摇码器（或电子计算机，例如：SPSS、Excel的特定函数、订制程序等），自动地逐个摇出（或电子计算机生成）一定数目的号码编成表，以备查用。
这个表内任何号码的出现，都有同等的可能性。利用这个表抽取样本时，可以大大简化抽样的繁琐程序。
缺点：不适用于总体中个体数目较多的情况。

1.2 基本步骤

随机号码表法应用的具体步骤是：

将调查总体单位/样本一一编号；
准备随机数表
在随机号码表上任意规定抽样的起点和抽样的顺序；
依次从随机号码表上抽取样本单位号码。
凡是抽到编号范围内的号码，就是样本单位的号码，一直到抽满为止。

1.3 案例1：利用随机数表抽样生成1个抽样组 / 重复抽样与不重复抽样

例如，某企业要调查消费者对某产品的需求量，要从95户居民家庭中抽选10户居民码表法抽选样本。

具体步骤如下：

第1步：将95户居民家庭编号，每一户家庭一个编号，即01～95。（每户居民编号为2位数）
第2步：准备随机数表。（利用计算机Excel软件生成的方法）

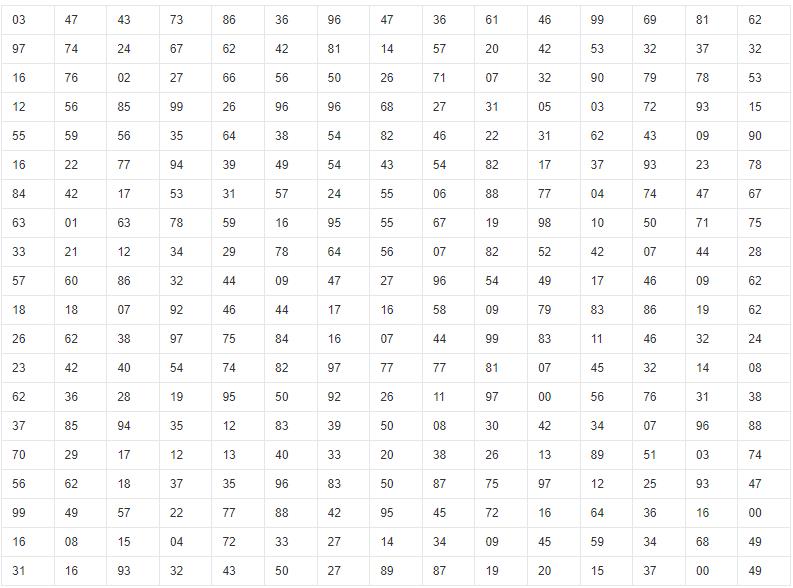
第3步：在上面的随机数表中，随机确定抽样的起点和抽样的顺序。假定从第1行，第6列开始抽，抽样顺序从左往右抽。（横的数列称“行”，纵的数列称为“列”。因此，此处第1行第6列为数字3。）

抽样的顺序：可从左往右、可从上到下

第4步：依次抽出号码，由此产生10个样本单位号码为：37、38、63、69、64、73、66、14、69、16。编号为这些号码的居民家庭就是抽样调查的对象。

备注说明： 重复抽样

编号69的居民家庭两次出现在样本里。这属于重复抽样。

所谓【重复抽样】，是指总体中某一单位被抽中作为样本后，再放回总体中，有可能第二次被抽中作为样本。

不重复抽样

不重复抽样，是指总体中的每个单位只可能抽中一次作为样本。即：某一单位抽中作为样本后，不能再放回总体中，也就没有可能第二次被抽中作为样本。

上例中若要求是不重复抽样，做法如下：
从16继续往后抽，接下来的96、98两个号码不在总体编号范围内，排除在外。然后，是16，仍有重复，排除在外。再接下来是29，没有重复，可以入选。
这样最终的10个样本单位号码就应是：37、38、63、69、64、73、66、14、16、29。

上中，若调查总体改为800户居民，样本数仍为10户，抽样起点为第3行，第1列，抽样顺序为从上往下抽。这10户样本居民号码如何产生呢？
首先，对调查总体800户居民编号，从001～800。（每户居民家庭号码为三位数）。
其次，抽样起点应为“167”，从上往下抽，
最后，依次产生的10户样本单位编号分别是：167、125、555、162、630、332、576、181、266、234。

1.4 案例2：完全随机设计

完全随机设计（completely random design）是采用完全随机化的分组方法，将全部的研究对象分配到n个处理组（比如，n=2，就是对照组和干预组；n=3，就是对照组、干预组1和干预组2.......），每组分贝接受不同的处理（干预），等干预结束后，比较各个组均数之间的差别有无统计学意义，以来推断干预是否有效果。

案例: 为了要研究升温毯联合自发热贴的主动保温措施在老年前列腺电切术中保温的应用效果。按照统一的纳入和排除标准选择100例行前列腺电切术老年患者进行双盲试验。问应该如何进行分组？

分组方法与步骤：

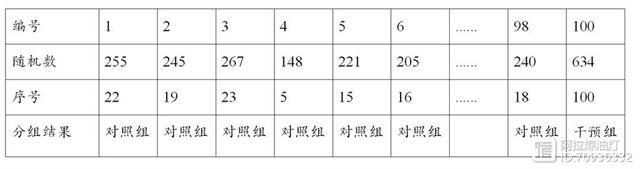
首先，将100例老年患者从1开始编号到100（下表第一行）；
然后，从随机数字表中的任一行任一列开始，如从第2行第5列开始，以此读取3位数作为一个随机数录入编号下面（下表第二行）；
接着，再将全部选出的随机数从小到大进行编序号（随机数相同的按照先手顺序编号），记录在第三行（下表）；
最后，我们规定序号1~50为对照组，序号51~100位干预组/试验组。

分组的方法：

1）根据对随机数排序后的有序序号，直接切分成N组(1-5、6-10、11-15、...)；

2）取模法：随机数%N，N是分组总数；对随机数取模数(%)，例如，总共要分成2组(取模的结果中，0代表第一组，1代表第二组)，随机数033取模033%2＝1，表示033随机数对应的样本被分到了第二组

3）N=2(特殊情况)时：随机数是单数的分到甲组，双数分到乙组；随机数033是单数，分甲组、随机数168是双数，分到乙组。

这样就分组完成了。

所以，大家在看到有一些文献中提到“按照随机数字表法”进行分组，其实就是这样去分组的，分组方法可能在文献中仅仅一笔，但是分组的严格程序大家还是有必要知道和执行。

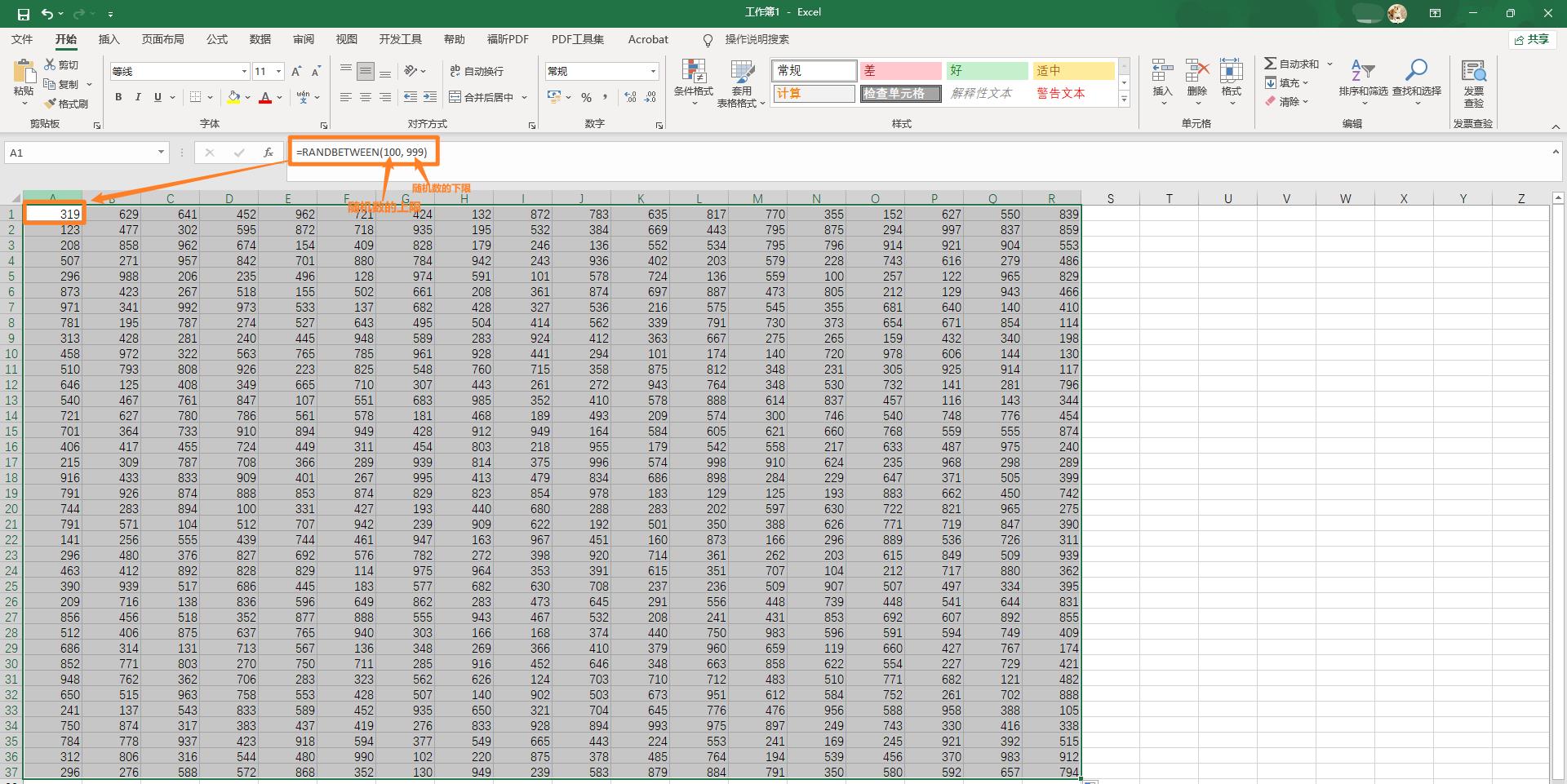
1.5 案例3：如何利用Excel快速产生随机数表?

参考文献

用Excel生成随机数表 - Weixin/统计学cwd

RANDBETWEEN(下限值, 上限值)

X 参考文献

本文作者：千千寰宇
本文链接： https://www.cnblogs.com/johnnyzen
关于博文：评论和私信会在第一时间回复，或直接私信我。
版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
声援博主：若本文对您有帮助，可点击右下角【推荐】一下。您的鼓励、【赞赏】（左侧赞赏支付码）是博主技术写作的重要动力！