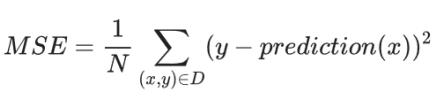单变量线性回归:TensorFlow 实战(理论篇)
Posted 小汤同学
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了单变量线性回归:TensorFlow 实战(理论篇)相关的知识,希望对你有一定的参考价值。
导语
慕课:《深度学习应用开发-TensorFlow实践》
章节:第五讲 单变量线性回归:TensorFlow 实战
这一讲里,将用一个简单的线性回归问题来讲解机器学习中的一些基本概念
监督式机器学习的基本术语
什么是机器学习?
机器学习系统通过学习如何组成输入信息来对从未见过的数据做出有用的预测
标签和特征
- 标签: 要预测的真实事物。在线性回归中,y就是标签
- 特征: 用于描述数据的输入变量。线性回归中的{X1,X2...Xn}就是特征
样本和模型
- 样本: 数据的特定实例
有标签样本:具有{特征,标签},用于训练模型
无标签样本:具有{特征,?},用于对新数据做出预测(或进行无监督学习)
- 模型: 将样本映射到预测标签,由模型的内部参数定义,这些内部参数值是通过学习得到的。
训练
训练模型表示通过有标签样本来学习(确定)所有权重和偏差的理想值。
在有监督学习中,机器学习算法通过以下方式构建模型:
检查多个样本并尝试找出可最大限度的减少损失的模型,这一过程称为经验风险最小化
损失
损失是对糟糕预测的惩罚:损失是一个数值,表示对于单个样本而言模型预测的准确程度
- 如果模型的预测完全准确,则损失为零,否则损失会比较大
- 训练模型的目标是从所有样本中找到一组平均损失较小的权重和偏差
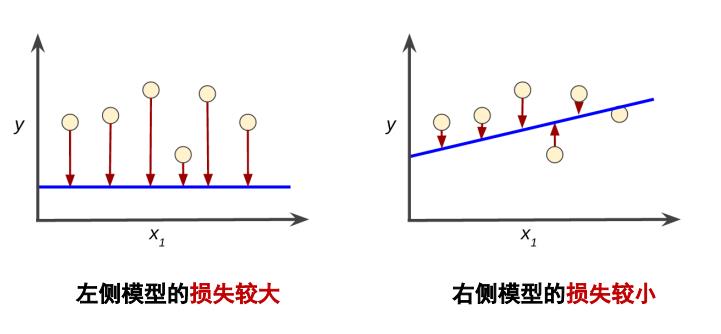
下图是一张损失的示意图,蓝线表示预测曲线,圆圈代表真实值。
常用的几种损失函数
- L1损失:基于模型预测的值与标签的实际值之差的绝对值
- 平方损失:一种常见的损失函数,又称为 L2 损失
- 均方误差 (MSE) :每个样本的平均平方损失
模型训练与降低损失
训练模型的迭代方法
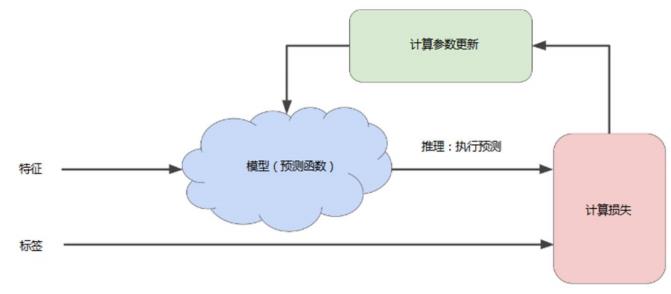
要点
- 首先对权重w和偏差b进行初始猜测
- 然后反复调整这些猜测
- 直到获得损失可能最低的权重和偏差为止
收敛
在学习优化过程中,机器学习系统将根据所有标签去重新评估所有特征,为损失函数生成一个新值,而该值又产生新的参数值。通常,可以不断迭代,直到总体损失不再变化或至少变化极其缓慢为止。这时候,我们可以说该模型已收敛
梯度下降法
梯度是什么?
一个向量(矢量),表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大
举个例子,看下面左边那张图,我们将损失曲线想象成右边的山坡,将损失下降想象成下山,那么梯度就可以想象成是下山的方向。
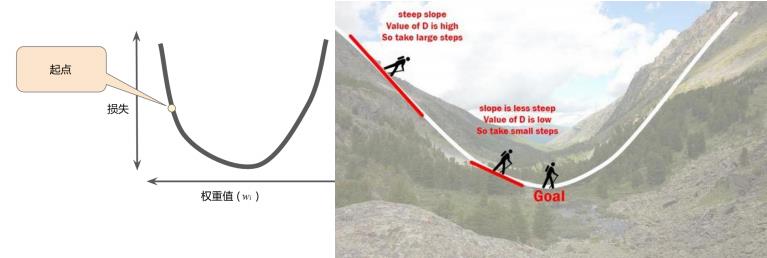
梯度是矢量,也就是说具有方向和大小,一般而言,我们沿着负梯度方向进一步向下探索
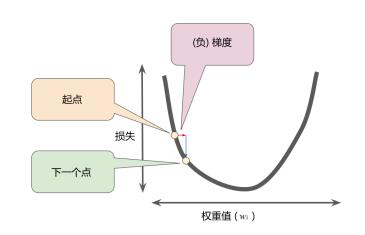
学习率
那么,问题来了,我们要尽快“下山”,我们一次应该前进多少呢?这就要引出学习率的概念。
在机器学习中,用梯度乘以一个称为学习速率(有时也称为步长)的标量,以确定下一个点的位置。
不过学习速率不能随意选择,要根据实际情况来选择,过大和过小都会出现问题。

超参数
在机器学习中,超参数是在开始学习过程之前设置值的参数,而不是通过训练得到的参数数据。
通常情况下,需要对超参数进行优化,选择一组好的超参数,可以提高学习的性能和效果。
超参数是编程人员在机器学习算法中用于调整的旋钮
典型超参数: 学习率、神经网络的隐含层数量……
具体实战请看实战篇:https://www.cnblogs.com/tangkc/p/15371698.html
学习笔记,仅供参考,如有错误,敬请指正!
同时发布在CSDN中:https://blog.csdn.net/tangkcc/article/details/120614863
以上是关于单变量线性回归:TensorFlow 实战(理论篇)的主要内容,如果未能解决你的问题,请参考以下文章