声学基础20210918课堂笔记
Posted prettysky
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了声学基础20210918课堂笔记相关的知识,希望对你有一定的参考价值。
Ch1.质点振动学
1.1质点振动系统的概念
集中参数系统:质量块的质量认为是集中在一点的,构成整个振动系统的质量块与弹簧的运动状态都是均匀的。
1.2质点的自由振动
| \\(M_{m}\\) | 坚硬物体的质量 |
| \\(K_{m}\\) | 弹簧的弹性系数或劲度系数 |
| \\(F_{k}\\) | 质点\\(M_{m}\\)上受到的弹簧弹力 |
| \\(C_{m}\\) | 弹簧的顺性系数或力顺 |
| \\(\\xi\\) | 质点离开平衡位置的位移 |
| \\(\\xi_{a}\\) | \\(\\xi\\)的振幅,位移振幅 |
| \\(\\xi_{st}\\) | 弹簧\\(K_{m}\\)在重力\\(M_{m}g\\)作用下产生的静位移 |
| \\(\\omega_{0}\\) | 振动圆频率或角频率 |
| \\(\\varphi_{0}\\) | 振动起始时刻的相位 |
1.2.1自由振动方程
胡克定律:\\(F_{k}=-K_{m}\\xi\\)
牛顿第二定律:\\(M_{m}\\frac{d^{2}\\xi}{dt^{2}}=-K_{m}\\xi\\)
引入一个参量振动圆频率\\(\\omega_{0}\\),改写:\\(\\frac{d^{2}\\xi}{dt^{2}}+\\omega_{0}^{2}\\xi=0\\)
上式称为质点的自由振动方程
自由振动的频率公式:\\(f_{0}=\\frac{1}{2\\pi}\\sqrt{\\frac{K_{m}}{M_{m}}}\\),称为系统的固有频率
降低固有频率的两个方法:1)增加系统的质量2)减少系统的弹性系数
弹簧质量对系统固有频率的影响
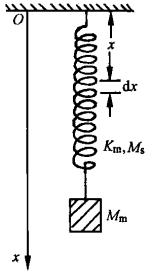
- 能量守恒定律:\\(E=E_{k}+E_{p}=C\\)
- \\(E_{p}=\\frac{1}{2}K_{m}\\xi^{2}\\)
- \\(E_{k}=E_{km}+E_{ks}\\)
- \\(E_{km}=\\frac{1}{2}M_{m}v^{2}\\)
- \\(dE_{ks}=\\frac{1}{2}(M_{s}\\frac{dx}{l})(v\\frac{x}{l})^{2}\\)
- \\(E_{ks}=\\int dE_{ks}=\\frac{1}{2}\\int_{0}^{l}(\\frac{M_{s}}{l^{3}}v^{2})x^{2}dx=\\frac{1}{6}M_{s}v^{2}\\)
- \\(\\frac{1}{2}(M_{m}+\\frac{M_{s}}{3})v^{2}+\\frac{1}{2}K_{m}\\xi^{2}=0\\)
- \\((M_{m}+\\frac{M_{s}}{3})\\frac{d\\xi^{2}}{dt^{2}}+K_{m}\\xi=0\\)
- \\(f_{0}=\\frac{1}{2\\pi}\\sqrt{\\frac{K_{m}}{M_{m}+\\frac{M_{s}}{3}}}\\)
- 即系统的总质量除了质量块的质量外,还附加了1/3的弹簧质量
考虑了弹簧质量后,固有频率变低
求系统的固有频率
质点静态平衡:\\(M_{m}g-K_{m}\\xi_{st}=0\\)
固有频率的另一种表达式:\\(f_{0}=\\frac{1}{2\\pi}\\sqrt\\frac{g}{\\xi_{st}}\\)
如果我们测出了系统的静位移\\(\\xi_{st}\\)就无需再知道系统的固有参量\\(M_{m}、K_{m}\\)
1.2.2自由振动的一般规律
质点的自由振动方程———对时间t的齐次二阶常微分方程
其一般解应是两个简谐函数的线性叠加\\(\\xi=Acos\\omega_{0}t+Bsin\\omega_{0}t\\)
也可以写为:\\(\\xi=\\xi_{a}cos(\\omega_{0}t-\\varphi_{0})\\),其中\\(A=\\xi_{a}cos\\varphi_{0},B=\\xi_{a}sin\\varphi_{0},\\varphi_{0}=arctan\\frac{B}{A},\\xi_{a}=\\sqrt{A^{2}+B^{2}}\\),表示简谐振动
知道了位移,也可以求振动速度\\(v=\\frac{d\\xi}{dt}=v_{a}sin(\\omega_{0}t-\\varphi_{0}+\\pi)\\),其中\\(v_{a}=\\omega_{0}\\xi_{a}\\)
若初始条件\\(\\xi_{(t=0)}=0,v=(\\frac{d\\xi}{dt})_{(t=0)}=v_{0}\\)
则质点的位移与速度为\\(\\xi=\\xi_{a}cos(\\omega_{0}t-\\frac{\\pi}{2}),v=v_{a}cos\\omega_{0}t\\),其中\\(\\xi_{a}=\\frac{v_{a}}{\\omega_{0}},v_{a}=v_{0}\\)
1.2.3自由振动的能量
能量保守系统
外部给予系统的能量,只有初动能:\\(E_{0}=\\frac{1}{2}M_{m}v_{0}^{2}\\)
系统的位能\\(E_{p}=\\int_{0}^{\\xi}K_{m}\\xi d\\xi=\\frac{1}{2}K_{m}\\xi^{2}\\)
系统所具有的动能\\(E_{k}=\\frac{1}{2}M_{m}v^{2}\\)
系统的总振动能\\(E=E_{p}+E_{k}=\\frac{1}{2}K_{m}\\xi^{2}+\\frac{1}{2}M_{m}v^{2}=\\frac{1}{2}K_{m}\\xi_{a}^{2}cos^{2}(\\omega_{0} t-\\varphi_{0})+\\frac{1}{2}M_{m}\\omega_{0}^{2}\\xi_{a}^{2}sin^{2}(\\omega_{0} t-\\varphi_{0})=\\frac{1}{2}K_{m}\\xi_{a}^{2}=\\frac{1}{2}M_{m}v_{a}^{2}\\)
已知有\\(v_{a}=v_{0}\\),证得\\(E=E_{0}\\)
1.2.4双弹簧串联与并联系统的振动
双弹簧串联
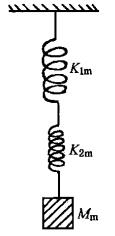
\\(M_{m}g=K_{1m}\\xi_{1st}=K_{2m}\\xi_{2st}\\)
\\(\\xi_{st}=\\xi_{1st}+\\xi_{2st}\\)
\\(\\xi_{st}=M_{m}g(\\frac{1}{K_{1m}}+\\frac{1}{K_{2m}})=M_{m}g\\frac{1}{K_{m}^{\'}}\\),其中\\(K_{m}^{\'}=\\frac{K_{1m}K_{2m}}{K_{1m}+K_{2m}}\\)
\\(f_{0}=\\frac{1}{2\\pi}\\sqrt{\\frac{g}{\\xi_{st}}}=\\frac{1}{2\\pi}\\sqrt{\\frac{K_{m}^{\'}}{M_{m}}}\\)
若两个相同的弹簧串联,可使系统的弹性减少一半,固有频率降低\\(\\sqrt{2}\\)倍
双弹簧并联
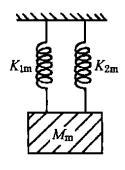
\\(M_{m}g=K_{1m}\\xi_{st}+K_{2m}\\xi_{st}\\)
\\(f_{0}=\\frac{1}{2\\pi}\\sqrt{\\frac{g}{\\xi_{st}}}=\\frac{1}{2\\pi}\\sqrt{\\frac{K_{m}^{\'\'}}{M_{m}}}\\)其中\\(K_{m}^{\'\'}=K_{1m}+K_{2m}\\)
若两个相同的弹簧并联,可使系统的弹性比单根时增加一倍,固有频率增加\\(\\sqrt{2}\\)倍
以上是关于声学基础20210918课堂笔记的主要内容,如果未能解决你的问题,请参考以下文章