从暴力递归到动态规划

Posted 2021-09-09 ThirtyFan

动态规划体会

整体思路

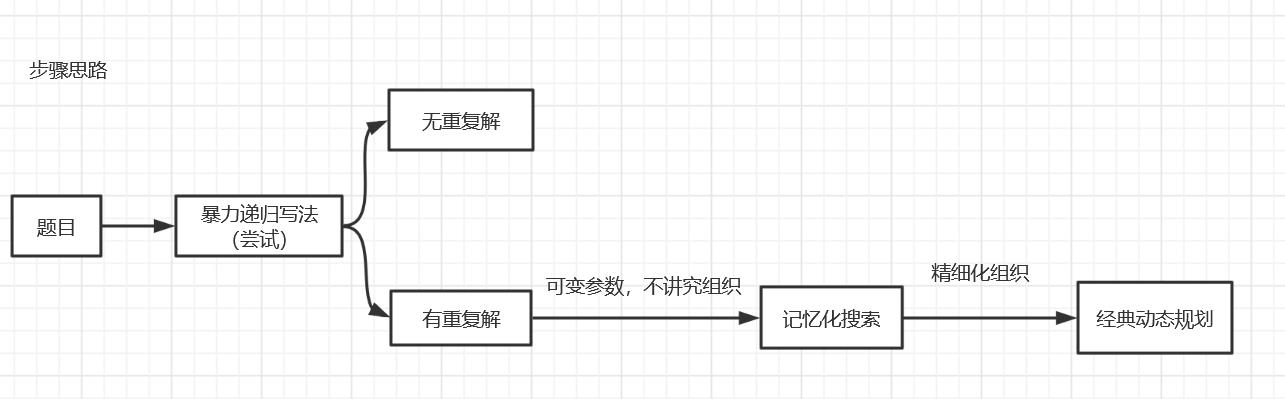
下面我们看一个栗子来充分理解从暴力递归到记忆化搜索再到经典动态规划的过程

栗子1：

有一个数组arr，均为正数且无重复值，每个值代表一个硬币的面值，例如arr[7，3，100，50]，每个面值有无数张，给定一个数值1000，问有多少种组合方法可以达到1000。

代码暴力递归：

    //arr中都是正数且无重复值，返回组成aim的方法数
    public static int  ways1(int[] arr,int aim) {
        if(arr == null || arr.length == 0 || aim<0) {
            return 0;
        }
        return process1(arr,0,aim);
    }
    //可以自由使用arr【index】所有的面值，每一种面值都可以使用任意张
    //组成rest，有多少种
    //重复解【10，100，50】: f(3,900)=0*10+1*100+0*50 = 5*10 + 0*100 + 0*50
    public static int process1(int[] arr,int index,int rest) {
        if(index == arr.length) {
            return rest == 0? 1:0;
        }
        int ways = 0;
        //i:张数
        for(int i = 0; i*arr[index] <= rest; i ++) {
            ways += process1(arr, index + 1, rest - (i*arr[index]));
        }
        return ways;
    }

代码记忆化搜索：

    //记忆化搜索
    public static int  ways2(int[] arr,int aim) {
        if(arr == null || arr.length == 0 || aim<0) {
            return 0;
        }
        int[][] dp = new int[arr.length + 1][aim+1];
        //初始化为-1
        for(int i = 0; i < dp.length; i ++) {
            for(int j = 0; j < dp[0].length; j ++) {
                dp[i][j] = -1;
            }
        }
        return process2(arr,0,aim,dp);
    }
  
    //dp[i][j] == -1说明这个值没有算过，否则算过，可直接返回
    //组成rest，有多少种
    public static int process2(int[] arr,int index,int rest,int[][] dp) {
        
        if(dp[index][rest] != -1) {
            return dp[index][rest];
        }
        
        if(index == arr.length) {
            dp[index][rest] = rest == 0? 1:0;
            return dp[index][rest];
        } 
        int ways = 0;
        //i:张数
        for(int i = 0; i*arr[index] <= rest; i ++) {
            ways += process2(arr, index + 1, rest - (i*arr[index]),dp);
        }
        dp[index][rest] = ways;
        return ways;
    }

代码经典动态规划：

 //经典动态规划，与记忆化搜索性能等效，因为存在枚举
    public static int  ways3(int[] arr,int aim) {
          if(arr == null || arr.length == 0 || aim<0) {
              return 0;
          }
          int N = arr.length;
          int[][] dp = new int[N + 1][aim+1];
          //index == arr.length的时候，rest为0则为1
          dp[N][0] =1;
          //接下来只要找到dp[index][rest]怎么表达就好
          //任何一个位置的dp[i][j]都与它下一层有关系
          for(int index = N-1; index >= 0; index --) {
              for(int rest = 0; rest <=aim; rest ++) {
                  int ways = 0;
                  //i:张数
                  for(int i = 0; i*arr[index] <= rest; i ++) {
                      ways += process1(arr, index + 1, rest - (i*arr[index]));
                  }
                  dp[index][rest] =  ways;
              }
          }
          return dp[0][aim];
      }

代码最终版本：

  //最终版本经典动态规划,枚举依赖下一个与左边一个
    public static int  ways4(int[] arr,int aim) {
          if(arr == null || arr.length == 0 || aim<0) {
              return 0;
          }
          int N = arr.length;
          int[][] dp = new int[N + 1][aim+1];
          //index == arr.length的时候，rest为0则为1
          dp[N][0] =1;
          
          //接下俩只要找到dp[index][rest]怎么表达就好
          //任何一个位置的dp[i][j]都与它下一层有关系
          for(int index = N-1; index >= 0; index --) {
              for(int rest = 0; rest <=aim; rest ++) {
                  dp[index][rest] =  dp[index+1][rest];
                  if(rest - arr[index] >= 0){
                      dp[index][rest] += dp[index][rest-arr[index]];
                  }
              }
          }
          return dp[0][aim];
      }

题目总结：这道题目充分展示了从暴力递归到经典动态规划的过程。因为在暴力递归中存在着重复解，所以我们采用一个数组dp来记录每一次计算的值，此时不考虑状态之间的依赖，单纯加入缓存，这就是记忆化搜索。然后我们考虑到了状态之间的依赖，我们发现任何一个位置的dp[i][j]都与它下一层有关系，只要知道dp[index][rest]怎么表达就可以改出来，此时与原题目已经没有关系，只要看着代码就可以改出来，这就是经典动态规划。再我们改完之后又发现存在着枚举，任何一个位置的dp[i][j]都等于dp[index+1][rest]加上左边的dp[index][rest-arr[index]]，所以改出了最终版本ways4。

记忆化搜索与动态规划的区别是力度上的不同，有些情况记忆化搜索比动态规划性能要好。如果本题中arr[100,1000,500],aim=100w，这种情况我们很清楚个位与十位均为0，在经典动态规划中我们把参数做最细粒度的划分，其实很多值在暴力递归中实际用不到的位置，而记忆化搜索是计算了哪些值我们存起来，下次要用再取，这种情况记忆化搜索就要比动态规划性能要好。我们再看一个栗子来深入体会一下。

栗子2：

给定一个字符串str，给定一个字符串类型的数组arr。arr里的每一个字符串，代表一张贴纸，你可以把单个字符剪开使用，目的是拼出str来。返回需要至少多少张贴纸可以完成这个任务。

栗子：str="babac",arr=["ba","c","abcd"] 至少需要俩张贴纸"ba"和"abcd"，因为使用这俩张贴纸，把每一个字符单独剪开，至少需要2个a，2个b，1个c。是可以拼出str的，所以返回2

图解：

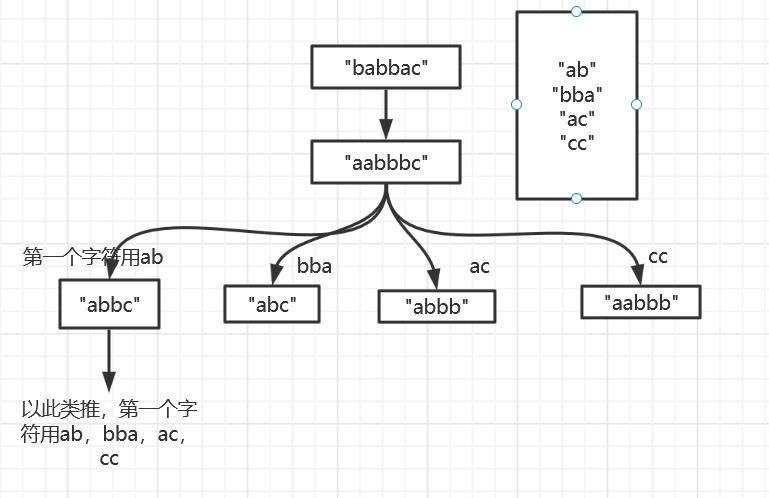
代码：

    public static int minStickers3(String[] stickers, String target) {
        int N = stickers.length;
        //将stickers中的每个字符串转化为[26]的数组，一共26个字母所以大小26。例如"abcka" ->[2,1,1...1]->a出现2次，b出现1次，c出现1次,
        int[][] counts = new int[N][26];
        //生成counts
        for (int i = 0; i < N; i++) {
            //str表示每个贴纸的每个字符
            char[] str = stickers[i].toCharArray();
            for (char cha : str) {
                //cha - \'a\':每个字母对应的ascii表,
                counts[i][cha - \'a\']++;
            }
        }
        //dp缓存
        HashMap<String, Integer> dp = new HashMap<>();
        dp.put("", 0);
        int ans = process3(counts, target, dp);
        return ans == Integer.MAX_VALUE ? -1 : ans;
    }
    
    //dp:缓存，如果t已经算过了，直接返回dp的值  t:剩余的目标
    public static int process3(int[][] map, String rest, HashMap<String, Integer> dp) {
        //算过直接返回
        if (dp.containsKey(rest)) {
            return dp.get(rest);
        }
        
        //词频统计，用tmap替代rest。转化过程rest = "aabbc" -->[2,2,1]
        char[] target = rest.toCharArray();
        int[] tmap = new int[26];
        for (char cha : target) {
            tmap[cha - \'a\']++;
        }
        
        int N = map.length;//贴纸数量
        int min = Integer.MAX_VALUE;//搞定rest使用的最少的贴纸数量
        
        for (int i = 0; i < N; i++) {
            int[] sticker = map[i];
            
            if (sticker[target[0] - \'a\'] > 0) {
                //i号贴纸，j枚举a~z。如果关于j这个字符tmap还有剩余，还剩余几个加入到builder里面。例如tmap[17],i[10]-->builder="aaaaaaa",7个a
                StringBuilder builder = new StringBuilder();
                for (int j = 0; j < 26; j++) {
                    if (tmap[j] > 0) {
                        int nums = tmap[j] - sticker[j];
                        for (int k = 0; k < nums; k++) {
                            builder.append((char) (j + \'a\'));
                        }
                    }
                }
                //i号贴纸已经搞定的字符去掉，剩余的字符存在builder里
                
                String s = builder.toString();
                min = Math.min(min, process3(map, s, dp));
            }
        }
        int ans = min + (min == Integer.MAX_VALUE ? 0 : 1);
        dp.put(rest, ans);
        return ans;
    }

 暴力递归和动态规划的关系

　　某一个暴力递归，有解的重复调用，就可以把这个暴力递归优化成动态规划。任何动态规划问题，都一定对应着某一个有解的重复调用的暴力递归，但不是所有的暴力递归，都一定对应着动态规划

暴力递归到动态规划的套路

1. 已经有了一个不违反原则的暴力递归，而且的确存在解的重复调用
2. 找到哪些参数的变化会影响返回值，对每一个列出变化范围
3. 参数间的所有的组合数量，意味着表大小
4. 记忆化搜索的方式就是傻缓存，非常容易得到
5. 规定好严表的大小，分析位置的依赖位置，然后从基础填写到最终解
6. 对于有枚举行为的决策过程，进一步优化