高精度

Posted 2021-08-25 离离原上谱一卷一枯荣

例1：791. 高精度加法

给定两个正整数，计算它们的和。

输入格式

共两行，每行包含一个整数。

输出格式

共一行，包含所求的和。

数据范围

1≤整数长度≤100000

输入样例：

12
23

输出样例：

35

#include <iostream>
#include <vector>

using namespace std;

vector<int> A, B, C;

//C = A + B
vector<int> add(vector<int> &A, vector<int> &B) {
    int t = 0;
    for (int i = 0; i < A.size() || i < B.size(); i ++) {
        if (i < A.size()) t += A[i];
        if (i < B.size()) t += B[i];
        C.push_back(t % 10);
        t /= 10;
    }
    if (t) C.push_back(t);
    return C;
}

int main() {
    string a, b;
    cin >> a >> b;
    
    for (int i = a.size() - 1; i >= 0; i --) A.push_back(a[i] - \'0\');
    for (int i = b.size() - 1; i >= 0; i --) B.push_back(b[i] - \'0\');
    
    C = add(A, B);
    
    for (int i = C.size() - 1; i >= 0; i --) cout << C[i];
    return 0;
}

 

例2：792. 高精度减法

给定两个正整数，计算它们的差，计算结果可能为负数。

输入格式

共两行，每行包含一个整数。

输出格式

共一行，包含所求的差。

数据范围

1≤整数长度≤10^5

输入样例：

32
11

输出样例：

21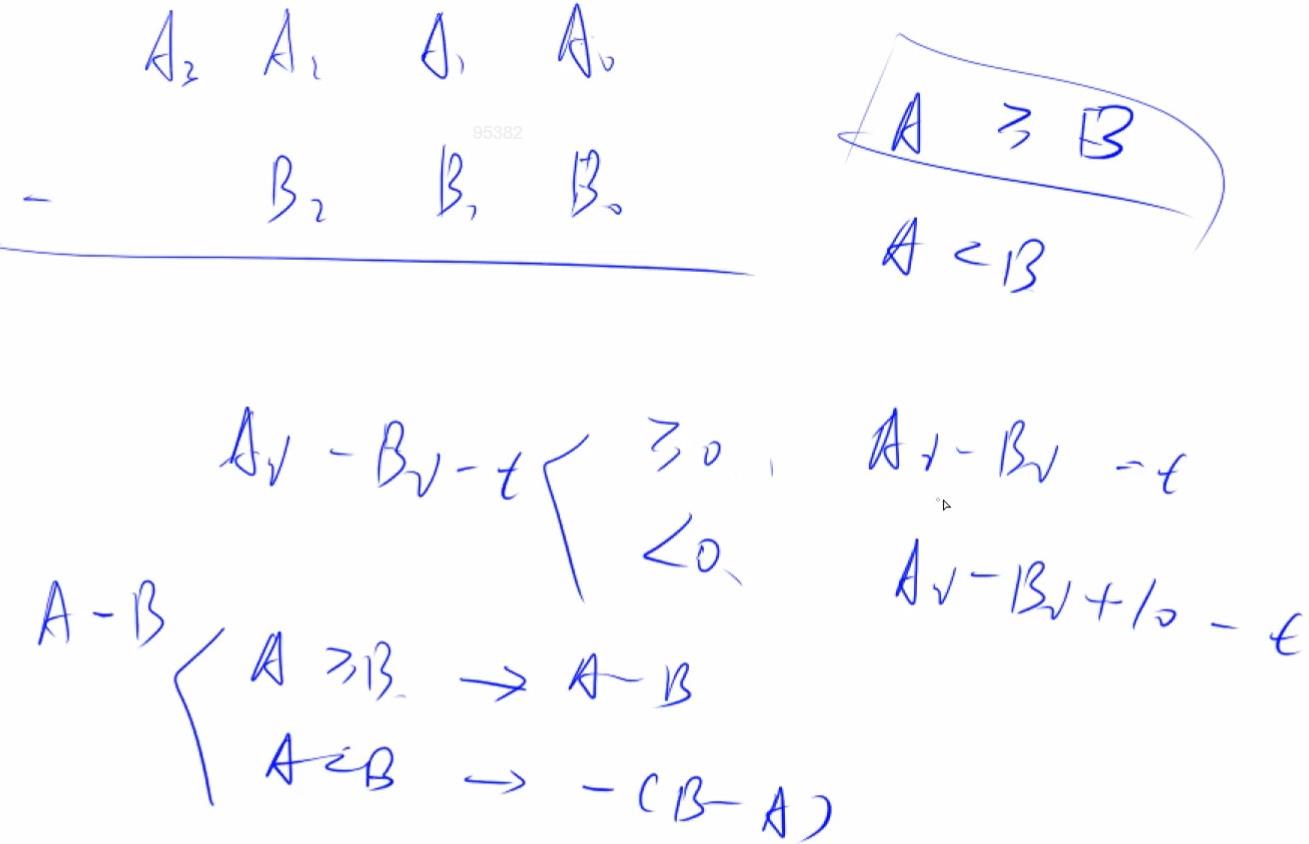

 

 

#include <iostream>
#include <vector>

using namespace std;

vector<int> A, B, C;

// 判断A是否>=B
bool cmp (vector<int> &A, vector<int> &B) {
    if (A.size() != B.size()) return A.size() > B.size();
    for (int i = A.size() - 1; i >= 0; i --) {
        if (A[i] != B[i]) return A[i] > B[i];
    }
    return true;
}

vector<int> sub(vector<int> &A, vector<int> &B) {
    for (int i = 0, t = 0; i < A.size(); i ++) {
        // t = A[i] - B[i] - t
        t = A[i] - t;
        if (i < B.size()) t -= B[i];
        C.push_back((t + 10) % 10);
        if (t < 0) t = 1;
        else t = 0;
    }
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

int main(){
    string a, b;
    cin >> a >> b;
    
    for (int i = a.size() - 1; i >= 0; i --) A.push_back(a[i] - \'0\');
    for (int i = b.size() - 1; i >= 0; i --) B.push_back(b[i] - \'0\');
    
    if (cmp(A, B)) {
        C = sub(A, B);
        for (int i = C.size() - 1; i >= 0; i --) cout << C[i];
    }
    else {
        C = sub(B, A);
        cout << \'-\';
        for (int i = C.size() - 1; i >= 0; i --) cout << C[i];
    }
    return 0;
}

 

例3：793. 高精度乘法

给定两个非负整数 A 和 B，请你计算 A×B 的值。

输入格式

共两行，第一行包含整数 A，第二行包含整数 B。

输出格式

共一行，包含 A×B 的值。

数据范围

1≤A的长度≤100000
0≤B≤100000

输入样例：

2
3

输出样例：

6

#include <iostream>
#include <vector>

using namespace std;

vector<int> mul(vector<int>& A, int b) {
    int t = 0;
    vector<int> C;
    for (int i = 0; i < A.size() || t; i ++) {
        t += A[i] * b;
        C.push_back(t % 10);
        t /= 10;
    }
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

int main() {
    string a;
    int b;
    cin >> a >> b;
    vector<int> A;
    for (int i = a.size() - 1; i >= 0; i --) A.push_back(a[i] - \'0\');
    auto C = mul(A, b);
    for (int i = C.size() - 1; i >= 0; i --) cout << C[i];
    return 0;
}

 

794. 高精度除法

给定两个非负整数 A B，请你计算 A/B 的商和余数。

输入格式

共两行，第一行包含整数 A，第二行包含整数 B。

输出格式

共两行，第一行输出所求的商，第二行输出所求余数。

数据范围

1≤A的长度≤100000,
1≤B≤10000
B 一定不为 0

输入样例：

7
2

输出样例：

3
1

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

vector<int> div (vector<int> A, int b, int &r) {
    r = 0;
    vector<int> C;
    for (int i = A.size() - 1; i >= 0; i --) {
        r = r * 10 + A[i];
        C.push_back(r / b);
        r %= b;
    }
    reverse(C.begin(), C.end());
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

int main() {
    string a;
    int b;
    cin >> a >> b;
    vector<int> A;
    int r;
    for (int i = a.size() - 1; i >= 0; i --) A.push_back(a[i] - \'0\');
    auto C = div(A, b, r);
    for (int i = C.size() - 1; i >= 0; i --) cout << C[i];
    cout << endl << r << endl;
    return 0;
}