leetcode 最短无序连续子数组 中等

Posted 2021-08-25 Wh1t3zZ

 

 

 

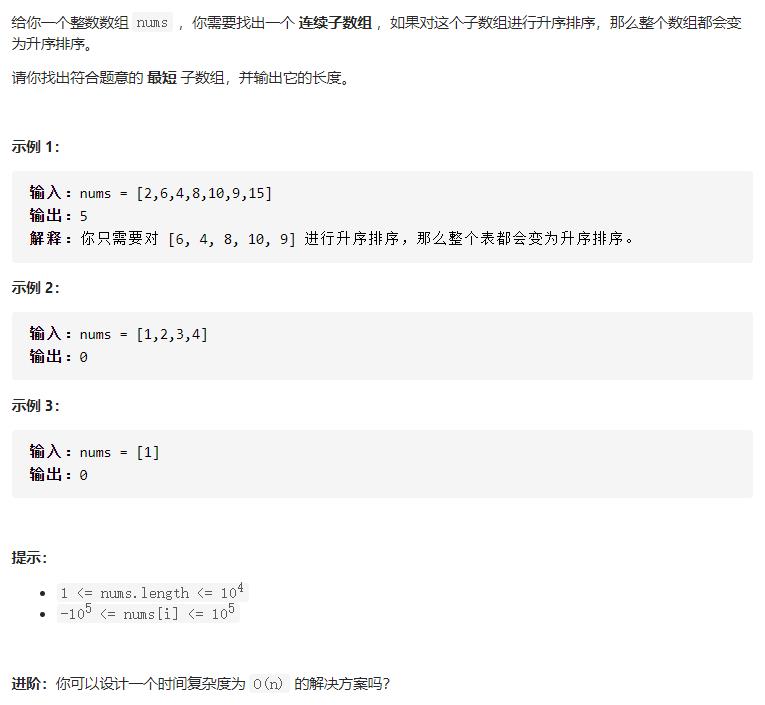
贪心：可以通过确定左右边界来获得答案。

确定左边界：如果一个下标 i，满足 nums[i] = min(nums[i], ... nums[n - 1])，那么这个 i 不然不在答案里，所以 ++ i 即可。

确定右边界：同理，如果一个下标 i，满足 nums[i] = max(nums[0], ... num[i])，那么这个 i 不然不在答案里，所以 -- i 即可。

所以可以有以下代码：

class Solution {
public:
    int findUnsortedSubarray(const vector<int>& nums) {
        if(nums.empty()) return 0;
        vector<int> minn(nums.size(), INT_MAX), maxx(nums.size(), INT_MIN);
        minn.back() = nums.back();
        maxx[0] = nums[0];
        for(int i = nums.size() - 2; i >= 0; -- i) {
            minn[i] = min(minn[i + 1], nums[i]);
        }
        for(int i = 1; i < nums.size(); ++ i) {
            maxx[i] = max(maxx[i - 1], nums[i]);
        }
        int l = 0, r = nums.size() - 1;
        while(l < nums.size() && nums[l] == minn[l]) {
            ++ l;
        }
        while(r >= 0 && nums[r] == maxx[r]) {
            -- r;
        }
        return r - l + 1 > 0 ? r - l + 1 : 0;
    }
};

 

然后其实可以不用到数组，即空间可以优化为 O(1)：

拿获得左边界为例：从后往前记录当前的最小值，如果 nums[i] > minn 了，更新一下最左边界就行。

然后这样写有个注意的点####：retL 与 retR 的初始值要满足 retR - retL + 1 <= 0 才行，以避免 {1, 2, 3, 4} 这种，retL 与 retR 根本不会被更新

class Solution {
public:
    int findUnsortedSubarray(const vector<int>& nums) {
        if(nums.empty()) return 0;
        int l = nums.size() - 1, retL = 0;
        int minn = INT_MAX;
        while(l >= 0) {
            if(nums[l] > minn) {
                retL = l;
            }
            minn = min(minn, nums[l]);
            -- l;
        }
        int r = 0, retR = -1;
        int maxx = INT_MIN;
        while(r < nums.size()) {
            if(nums[r] < maxx) {
                retR = r;
            }
            maxx = max(maxx, nums[r]);
            ++ r;
        }
        return retR - retL + 1 > 0 ? retR - retL + 1 : 0;
    }
};