一文看懂从并查集到图的基本算法
Posted ThirtyFan
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了一文看懂从并查集到图的基本算法相关的知识,希望对你有一定的参考价值。
并查集
并查集思路:
- 有若干个样本a,b,c,d...假设类型都是V
- 在并查集中一开始认为每个样本都在单独的集合里
- 用户可以在任何时候调用俩个方法:boolean isSameSet(V x,V y):查询样本x和样本y是否属于一个集合;boolean union(V x,V y):把x和y各自所在的集合的所有样本合并成一个集合,把小集合的头节点直接连到大集合的头节点上
- isSameSet和union的代价越低越好
图解
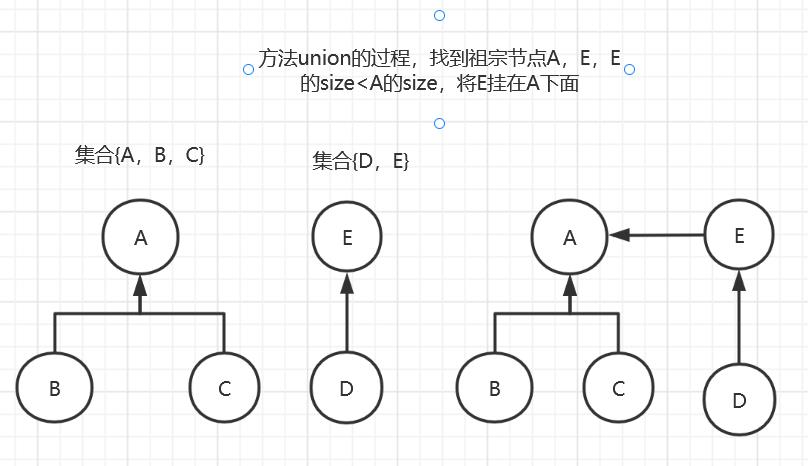
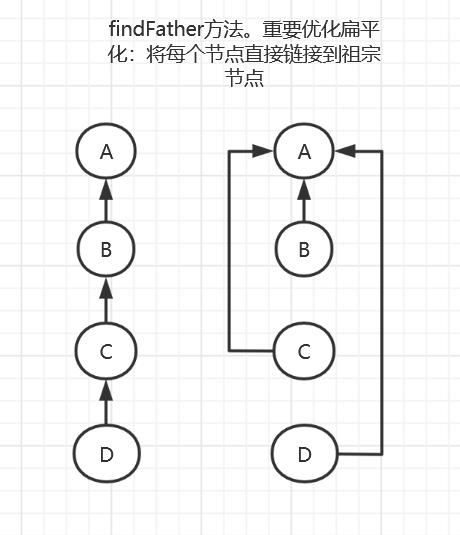
代码
方法:
UnionFind:初始化一个节点
findFather:找到某个节点的祖宗节点
isSameSet:判断俩个节点是否在一个集合
union:俩个集合进行合并
public class Test { public static class Node<V> { V value; public Node(V v) { value = v; } } public static class UnionFind<V> { //V---->节点 public HashMap<V, Node<V>> nodes; //K某个节点--->value祖宗节点 public HashMap<Node<V>, Node<V>> parents; //K祖宗节点--->value以该节点为头节点的集合的大小 public HashMap<Node<V>, Integer> sizeMap; //初始化过程:将所有样本放在List<V> values V{a,b,c,d,e} --->{a}{b}{c}{d}{e} public UnionFind(List<V> values) { nodes = new HashMap<>(); parents = new HashMap<>(); sizeMap = new HashMap<>(); for (V cur : values) { //每个值做成一个node Node<V> node = new Node<>(cur); nodes.put(cur, node); parents.put(node, node); sizeMap.put(node, 1); } } //给你一个节点,找到祖宗节点,把组总结点返回。重要优化把整个链打扁平 public Node<V> findFather(Node<V> cur) { Stack<Node<V>> path = new Stack<>(); //跳出这个while时cur就是祖宗节点 while (cur != parents.get(cur)) { path.push(cur); cur = parents.get(cur); } //cur祖宗节点,path里面存着沿途路径的每个节点 while (!path.isEmpty()) { parents.put(path.pop(), cur); } return cur; } //如果a样本跟b样本的祖宗节点一样就是一个集合 public boolean isSameSet(V a, V b) { return findFather(nodes.get(a)) == findFather(nodes.get(b)); } //将a集合与b集合合并 public void union(V a, V b) { Node<V> aHead = findFather(nodes.get(a)); Node<V> bHead = findFather(nodes.get(b)); if (aHead != bHead) { int aSetSize = sizeMap.get(aHead); int bSetSize = sizeMap.get(bHead); //big表示大集合的祖宗节点 Node<V> big = aSetSize >= bSetSize ? aHead : bHead; //small表示小集合的祖宗节点 Node<V> small = big == aHead ? bHead : aHead; parents.put(small, big); sizeMap.put(big, aSetSize + bSetSize); sizeMap.remove(small); } } public int sets() { return sizeMap.size(); } } }
举栗子:
如果俩个user,a字段一样,或者b字段一样,或者c字段一样,就认为是一个人。
请合并users,返回合并之后的用户数量
图解:
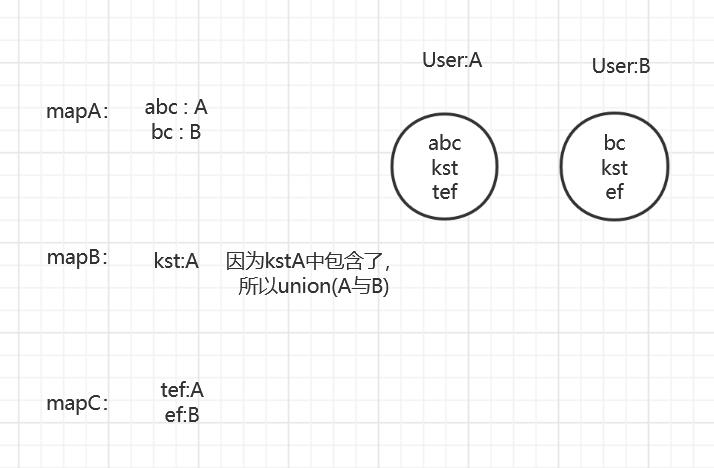
代码:
public static class User{ public String a; public String b; public String c; public User(String a, String b, String c) { super(); this.a = a; this.b = b; this.c = c; } } //题目:如果俩个user,a字段一样,或者b字段一样,或者c字段一样,就认为是一个人 //请合并users,返回合并之后的用户数量 public static int mergeUsers(List<User> users) { UnionFind<User> unionFinds = new UnionFind(users); HashMap<String,User> mapA= new HashMap<>(); HashMap<String,User> mapB= new HashMap<>(); HashMap<String,User> mapC= new HashMap<>(); for(User user : users) {
//如果mapA中包含这个用户的a字段,则进行合并,不包含则添加到mapA中 if(mapA.containsKey(user.a)) { unionFinds.union(user, mapA.get(user.a)); }else { mapA.put(user.a, user); } if(mapB.containsKey(user.b)) { unionFinds.union(user, mapB.get(user.b)); }else { mapB.put(user.b, user); } if(mapC.containsKey(user.c)) { unionFinds.union(user, mapC.get(user.c)); }else { mapC.put(user.c, user); } } return unionFinds.getSetNum(); }
图
基本介绍:
- 由点的集合和边的集合构成
- 虽然存在有向图和无向图的概念,但实际上都可以用有向图来表示
- 边上带有权值
图结构的表达
图结构的表达有很多种方式,例如邻接表法,邻接矩阵

所以可以找一种自己熟悉的结构,把题目中给的结构转化为自己熟悉的结构:
代码:
点结构的描述
// 点结构的描述 value: 编号 in:入度个数 out:出度个数 nexts:出度的直接邻居 edges:边结构 public class Node { public int value; public int in; public int out; public ArrayList<Node> nexts; public ArrayList<Edge> edges; public Node(int value) { this.value = value; in = 0; out = 0; nexts = new ArrayList<>(); edges = new ArrayList<>(); } }
边结构描述
//weight:权重 from: 出发的点 to:到达的点 public class Edge { public int weight; public Node from; public Node to; public Edge(int weight, Node from, Node to) { this.weight = weight; this.from = from; this.to = to; } }
图结构描述
public class Graph { //由点集与边集构成 HashMap:key 编号 value:点结构 public HashMap<Integer, Node> nodes; public HashSet<Edge> edges; public Graph() { nodes = new HashMap<>(); edges = new HashSet<>(); } }
常见的图结构有如下表达:
[[7,0,4] [4,1,3] [3,2,3] [8,2,4]] ------>[权值,from,to]
将这种结构转化为自己上面我们所述的图结构
代码:
/* * N*3 的矩阵转为为我们熟悉的图结构过程 * [5,0,7] [3,0,1][weight,from节点上面的值,to节点上面的值] */ public static Graph createGraph(int[][] matrix) { Graph graph = new Graph(); for (int i = 0; i < matrix.length; i++) { // 拿到每一条边, matrix[i] int weight = matrix[i][0]; int from = matrix[i][1]; int to = matrix[i][2]; //如果图结构的点集没有from这个点,在图结构中的点集中添加 if (!graph.nodes.containsKey(from)) { graph.nodes.put(from, new Node(from)); } if (!graph.nodes.containsKey(to)) { graph.nodes.put(to, new Node(to)); } //可以拿到from编号所对应的点,to编号所对应的点,以及边 Node fromNode = graph.nodes.get(from); Node toNode = graph.nodes.get(to); //这条边从from点出发到to点 Edge newEdge = new Edge(weight, fromNode, toNode); //添加from点的直接邻居 fromNode.nexts.add(toNode); fromNode.out++; toNode.in++; //将这条边添加到from的直接边的集合中 fromNode.edges.add(newEdge); graph.edges.add(newEdge); } return graph; }
图的宽度优先遍历(bfs)
基本思路
- 利用队列实现
- 从源节点依次按照宽度进队列,然后弹出
- 没弹出一个节点,把该节点所有没有进过队列的邻接点放入队列
- 直到队列变空
图解
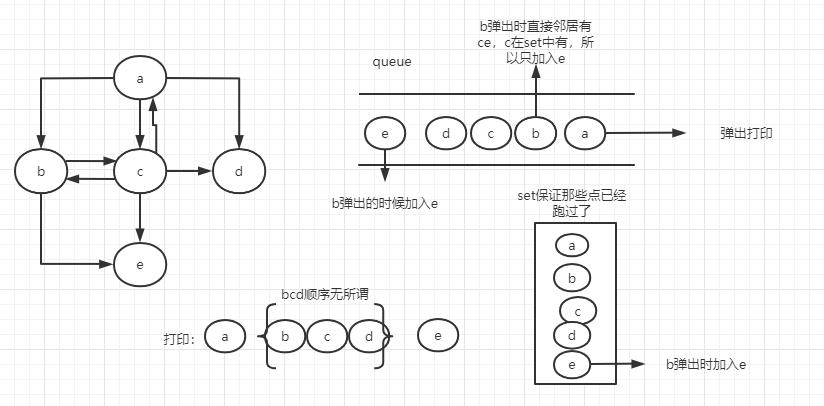
代码
//从node出发,进行宽度优先遍历,一层一层遍历 //在二叉树中bfs不用set,因为二叉树没有环的问题 public static void bfs(Node start) { if (start == null) { return; } Queue<Node> queue = new LinkedList<>(); HashSet<Node> set = new HashSet<>(); queue.add(start); set.add(start); while (!queue.isEmpty()) { //弹出打印 Node cur = queue.poll(); System.out.println(cur.value); //直接邻居没有进过set的加入set与queue,避免环 for (Node next : cur.nexts) { if (!set.contains(next)) { set.add(next); queue.add(next); } } } }
图的深度优先遍历(dfs)
基本思路
- 利用栈实现
- 从源节点开始把节点按照深度放入栈,然后弹出
- 每弹出一个节点,把该节点所有没有进过栈的邻接点放放入栈
- 直到栈变空
图解
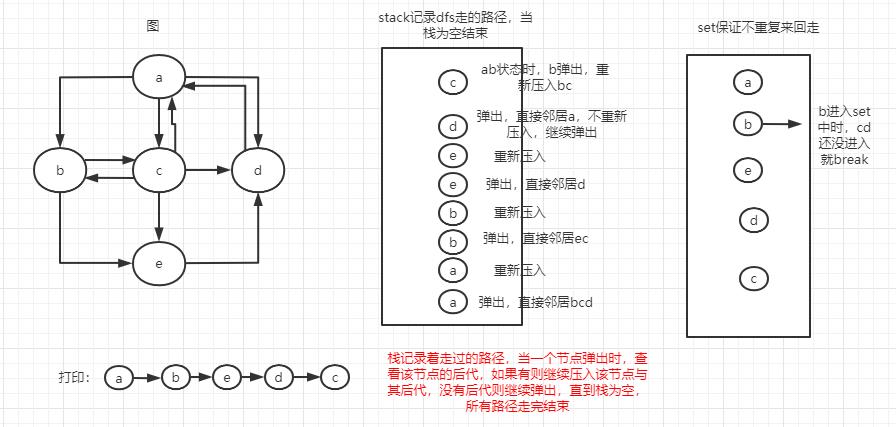
代码
//深度优先遍历一条路走到头,再往上返回 public static void dfs(Node node) { if (node == null) { return; } Stack<Node> stack = new Stack<>(); HashSet<Node> set = new HashSet<>(); stack.add(node); set.add(node); System.out.println(node.value); while (!stack.isEmpty()) { Node cur = stack.pop(); for (Node next : cur.nexts) { //如果后代没有进过栈,父压入栈,后代压入栈,打印,break if (!set.contains(next)) { stack.push(cur); stack.push(next); set.add(next); //进栈打印 System.out.println(next.value); break; } } } }
图的拓扑排序算法
基本思路:
- 在图中找到所有入度为0的点输出
- 把所有入度为0的点在图中删掉,继续找入度为0的点输出,周而复始
- 图的所有点都被删除后,依次输出的顺序就是拓扑排序
要求:有向图且没有环
应用:事件安排,编译顺序
图解:
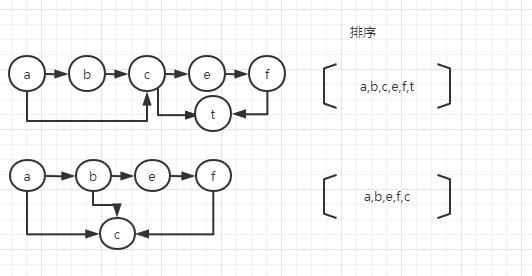
代码
public static List<Node> sortedTopology(Graph graph) { // key 某个节点 value 剩余的入度 HashMap<Node, Integer> inMap = new HashMap<>(); // 只有剩余入度为0的点,才进入这个队列 Queue<Node> zeroInQueue = new LinkedList<>(); //for结束会找出一个入度为0的点 for (Node node : graph.nodes.values()) { //原始图中每个点的原始入度数 inMap.put(node, node.in); if (node.in == 0) { zeroInQueue.add(node); } } //结果集 List<Node> result = new ArrayList<>(); while (!zeroInQueue.isEmpty()) { Node cur = zeroInQueue.poll(); result.add(cur); for (Node next : cur.nexts) { //cur所有邻居入度-1 inMap.put(next, inMap.get(next) - 1); if (inMap.get(next) == 0) { zeroInQueue.add(next); } } } return result; }
在学习kruskal与prim之前我们先了解一下什么是最小生成树,采用百度百科的介绍
一个有 n 个结点的连通图的生成树是原图的极小连通子图,且包含原图中的所有 n 个结点,并且有保持图连通的最少的边。
举栗子
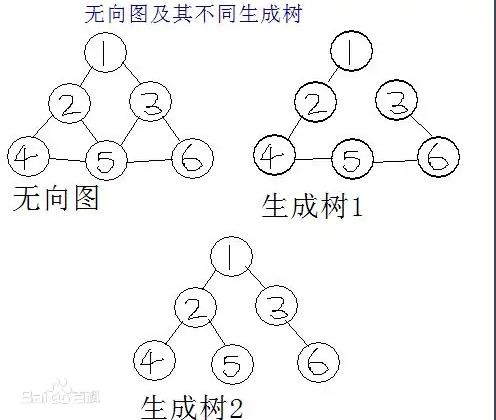
最小生成树之krusKal算法
基本思路:
- 总是从权值最小的变开始考虑,依次考察权值依次变大的边
- 当前的边要么进入最小生成树的集合,要么丢弃
- 如果当前的边进入最小生成树的集合中不会形成环,就要当前边
- 如果当前的边进入最小生成树的集合中会形成环,就不要当前边
- 考察完所有边之后,最小生成树的集合也得到了
图解
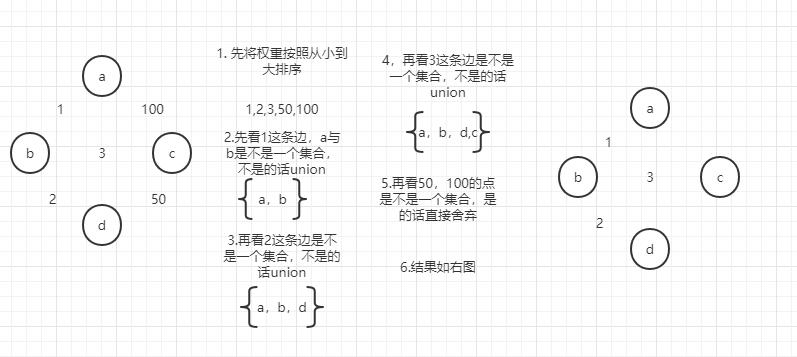
代码:
这里我们用到了前面的并查集,结果返回我们要的边的集合。这里做的是无向图,只是要最后的权值,如果是有向图的话会少一侧
public static class UnionFind { // key 某一个节点, value key节点往上的节点 private HashMap<Node, Node> fatherMap; // key 某一个集合的代表节点, value key所在集合的节点个数 private HashMap<Node, Integer> sizeMap; public UnionFind() { fatherMap = new HashMap<Node, Node>(); sizeMap = new HashMap<Node, Integer>(); } public void makeSets(Collection<Node> nodes) { fatherMap.clear(); sizeMap.clear(); for (Node node : nodes) { fatherMap.put(node, node); sizeMap.put(node, 1); } } private Node findFather(Node n) { Stack<Node> path = new Stack<>(); while(n != fatherMap.get(n)) { path.add(n); n = fatherMap.get(n); } while(!path.isEmpty()) { fatherMap.put(path.pop(), n); } return n; } public boolean isSameSet(Node a, Node b) { return findFather(a) == findFather(b); } public void union(Node a, Node b) { if (a == null || b == null) { return; } Node aDai = findFather(a); Node bDai = findFather(b); if (aDai != bDai) { int aSetSize = sizeMap.get(aDai); int bSetSize = sizeMap.get(bDai); if (aSetSize <= bSetSize) { fatherMap.put(aDai, bDai); sizeMap.put(bDai, aSetSize + bSetSize); sizeMap.remove(aDai); } else { fatherMap.put(bDai, aDai); sizeMap.put(aDai, aSetSize + bSetSize); sizeMap.remove(bDai); } } } } //边从小到大排序 public static class EdgeComparator implements Comparator<Edge> { @Override public int compare(Edge o1, Edge o2) { return o1.weight - o2.weight; } } public static Set<Edge> kruskalMST(Graph graph) { UnionFind unionFind = new UnionFind(); //先将图中的每个点做成一个集合 unionFind.makeSets(graph.nodes.values()); // 从小的边到大的边,依次弹出,小根堆! PriorityQueue<Edge> priorityQueue = new PriorityQueue<>(new EdgeComparator()); for (Edge edge : graph.edges) { // M 条边 priorityQueue.add(edge); // O(logM) } Set<Edge> result = new HashSet<>(); while (!priorityQueue.isEmpty()) { // M 条边 Edge edge = priorityQueue.poll(); // O(logM) //如果边的左右俩测不是同一个集合,要这条边,合并这俩个节点 if (!unionFind.isSameSet(edge.from, edge.to)) { // O(1) result.add(edge); unionFind.union(edge.from, edge.to); } } return result; } }
最小生成树之Prim算法
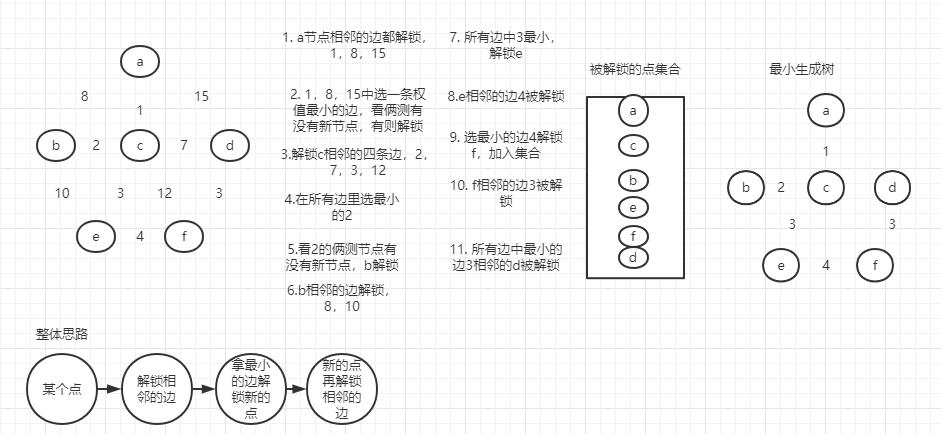
基本思路:
- 可以从任意节点出发来寻找最小生成树
- 某个点加入到被选取的点中后,解锁这个点出发的所有新的边
- 在所有解锁的边中选最小的边,然后看看这个边会不会形成环
- 如果会,不要当前边,继续考察剩下解锁的边中最小的边(重复3)
- 如果不会,要当前边,将该边的指向点加入到被选取的点中(重复2)
- 当所有点都被选取,最小生成树就得到了
图解:
代码
public static class EdgeComparator implements Comparator<Edge> { @Override public int compare(Edge o1, Edge o2) { return o1.weight - o2.weight; } } public static Set<Edge> primMST(Graph graph) { // 解锁的边进入小根堆 PriorityQueue<Edge> priorityQueue = new PriorityQueue<>(new EdgeComparator()); // 哪些点被解锁出来了 HashSet<Node> nodeSet = new HashSet<>(); // 依次挑选的的边在result里 Set<Edge> result = new HashSet<>();
//for循环防止森林 for (Node node : graph.nodes.values()) { // 随便挑了一个点 // node 是开始点 if (!nodeSet.contains(node)) { nodeSet.add(node); for (Edge edge : node.edges) { // 由一个点,解锁所有相连的边 priorityQueue.add(edge); } while (!priorityQueue.isEmpty()) { Edge edge = priorityQueue.poll(); // 弹出解锁的边中,最小的边 Node toNode = edge.to; // 可能的一个新的点 if (!nodeSet.contains(toNode)) { // 不含有的时候,就是新的点 nodeSet.add(toNode); result.add(edge); for (Edge nextEdge : toNode.edges) { priorityQueue.add(nextEdge); } } } } break; } return result; }
总结:
一开始介绍了并查集,主要就是俩个方法issameSet与union,先检查俩个节点是不是在一个集合中,如果不是的话我们要进行合并集合,小集合的头挂在大集合的头上。这里要注意的就是findFather这个方法,里面的重要优化是将整个链表
扁平化,这样我们再来一个新的节点找父节点的时候可以直接找到,不用遍历。
然后介绍了图结构,图结构有很多种,邻接矩阵,邻接链表等,这里列举了一种比较万能的图结构表达,可以将给定的图结构转化成我们熟悉的结构,列举了一个例子就是[[7,0,4] [4,1,3] [3,2,3] [8,2,4]] ------>[权值,from,to]。
接着介绍了图的宽度优先遍历bfs与深度优先遍历dfs。宽度优先遍历就是按照层的方式一层一层的往下遍历,这里需要注意的是与二叉树的bfs不同的是我们增加了一个set集合,主要是在二叉树中不存在环的问题,用set可以记录哪些节点已经
跑过了,不需要再跑。深度优先遍历就是一条路走到头,用栈记录着走过的路径,同样的set可以保证不重复来回走。
拓扑排序是有前提的,有向图并且没有环。主要思路就是在图中找到所有入度为0的点输出,然后把所有入度为0的点在图中删掉,继续找入度为0的点输出,周而复始,直到图中所有的点被删掉为止。
最小生成树介绍了krusKal算法与Prim算法。krusKal用到了前面介绍的并查集,思路还是比较简单的。我们先把所有的边放入小根堆进行从小到大排序,然后每弹出一个看一下边左右俩测节点是不是同一个集合,是的话继续弹出,不是的话合并
这俩个节点,直到小根堆中没有边为止。Prim主要思路是先随便找一个点,然后解锁它锁相邻的边,在里面选一条最小的边然后解锁新的节点,这个新的节点又可以解锁相邻的边,周而复始,直到所有的点都解锁为止。难懂的地方可能是那个for
循环,主要是用来防止森林的,平时可能用不到,删掉也可以,同样这里我们也利用一个set集合用来记录哪些点被解锁了。
另外可能图解画的不是很清楚,需要很仔细的看,我会努力提高画图的能力。笑。以上代码均来自左神,不认识的可以去百度,真的是讲的非常好的一位老师。这里有写的不对的地方,欢迎指出,我们共同进步。
以上是关于一文看懂从并查集到图的基本算法的主要内容,如果未能解决你的问题,请参考以下文章