二分搜索算法

Posted 2021-08-16

二分搜索算法

常用的使用场景：寻找一个数，寻找左侧边界，寻找右侧边界

1.1 二分搜索模板

先介绍下二分搜索模板，后面的二分搜索都是基于这个二分搜索模板的

int binarySearch(vector<int>& nums, int target){
    int left = 0, right = ...; // right = nums.size()  还是 right = nums.size() - 1
    while(...){ // left < right  还是 left <= right
        int mid = left + (right - left) / 2; //防止溢出  mid = (left + right) / 2;可能出现溢出
        if(nums[mid] == target) ... ;
        else if(nums[mid] < target) left = ... ;
        else if(nums[mid] > target) right = ... ;
    }  
    return ...;  
}

说明：

1. 分析二分搜索代码时，不要出现else，全部展开成else if，方便理解
2. ...的地方是需要详细说明的细节
3. mid = (left + right) / 2 可能出现溢出， 为了防止溢出 mid = left + (right - left) / 2；

1.2 寻找一个数(基本的二分搜索)

场景：搜索一个数，如果存在，则返回索引，否则返回-1

在此之前，先简单提下搜索区间这个概念，二分搜索的变形一般分有左闭右闭和左闭右开两种搜索区间

左闭右闭区间

int binarySearch(vector<int>& nums, int target){
    if(nums.size() == 0) return -1;
    int left = 0, right = nums.size() - 1; //注意 right
    while(left <= right){ //注意 <=
        int mid = mid = left + (right - left) / 2;
        if(nums[mid] == traget) return mid;
        else if(nums[mid] < target) left = mid + 1; // 注意
        else if(nums[mid] > target) right = mid - 1; // 注意
    }
    return -1;
}

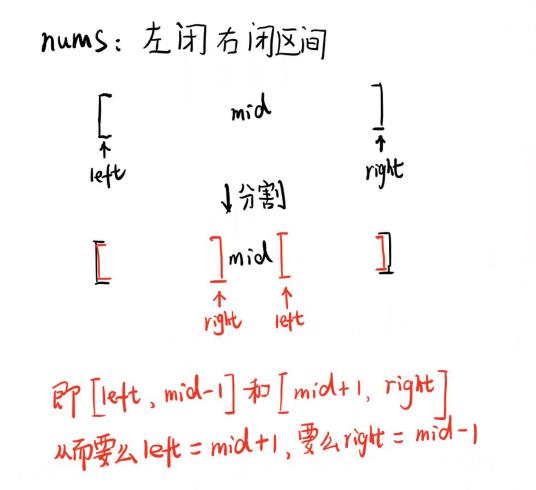
首先 left 和 right 指针 分别指向数组的首尾元素，都是可以取到的，我们称这个二分的搜索区间为左闭右闭区间，即[left, right]，这个区间其实就是每次进行搜索的区间，那么当区间为空的时候就终止搜索，那么啥时候区间刚好终止呢？答案是left = right + 1的时候，区间变为[right + 1， right]，这个区间为空。举个例子[2， 2]区间还存在数字2，而[3， 2]这个区间是不存在的。所以while的循环条件应该是left <= right，其终止条件正好是left == right + 1，区间为空（而不是left < right，它的终止条件是left == right 区间非空）。下面开始搜索mid是否为查找的目标值，是就返回mid，不是就应该去掉mid分割成两个区间，而且应该保证这两个区间也是左闭右闭区间，那么只有分成[left， mid - 1] 和 [mid + 1， right]两种，这也就确定了后面left 和 right 的更新。当没搜索到目标值时，返回-1；

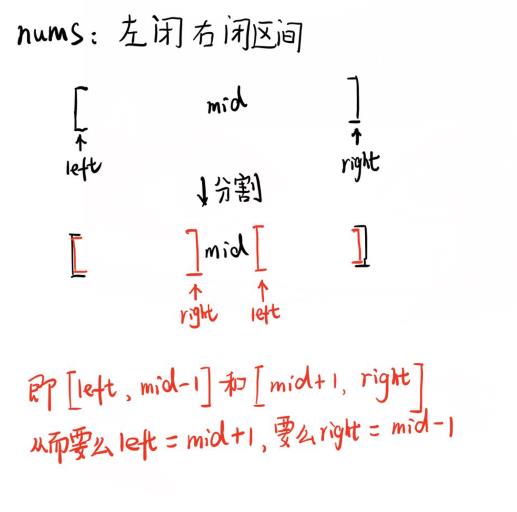
左闭右开区间

int binarySearch(vector<int>& nums, int target){
    if(nums.size() == 0) return -1;
    int left = 0, right = nums.size(); //注意 right
    while(left < right) { //注意 <
        int mid = mid = left + (right - left) / 2;
        if(nums[mid] == target) return mid;
        else if(nums[mid] < target) left = mid + 1; // 注意
        else if(nums[mid] > target) right = mid; //注意
    }
    //while循环的终止条件 left == right
    return -1;
}

首先 left 和 right 指针 分别指向数组的首元素和末尾元素的后一位，显然right是取不到数组中元素的，我们称这个二分搜索区间为左闭右开区间， 即[left ，right)，这个区间其实就是每次进行搜索的区间，那么当区间为空的时候就终止搜索，那么啥时候区间刚好终止呢？答案是当left == right的时候，举个例子区间[2， 2）显然不存在。所以while循环条件应该是left < right，其终止条件正好是left == right，区间为空（为啥不是<=呢， 因为此时不是临界条件，不满足刚好停止）。下面开始搜索mid是否为查找的目标值，是就返回mid，不是就应该去掉mid分割成两个区间，而且应该保证这两个区间也是左闭右开区间，那么只有分割成[left，mid) 和 [mid + 1，right），这也就确定了后面left 和 right 的更新。当没搜索到目标值时，返回-1；

但是上面两种算法存在局限性，比如，提供有序数组nums = [1, 3, 3, 3, 4]，target = 3，则该算法返回的是正中间的索引2。但是如果我们想找到target的左侧边界，即索引1，或者想找到target的右侧边，即索引3，则算法是无法处理的，下面就介绍算法的改进

1.3 寻找左侧边界的二分搜索

提供两种写法

左闭右闭区间

int left_bound(vector<int>& nums, int target){
    if(nums.size() == 0) return -1;
    int left = 0, right = nums.size() - 1; //左闭右闭区间[left, right]
    while(left <= right){ //循环终止条件left == right + 1, [right + 1, right]区间为空 
        int mid = mid = left + (right - left) / 2;
        if(nums[mid] == target) right = mid - 1; // 注意
        else if(nums[mid] < target) left = mid + 1;
        else if(nums[mid] > target) right = mid - 1;
    }
   	// while 循环退出的条件 left == right + 1
    // 当target比nums中所有元素大时，left会索引越界
    // 当target比nums中所有元素小时，right会索引越界，left刚好指向第一个元素
    // 当target不在数组中，且不满足上述两种情况，则left会指向某个元素，其索引为x，其特殊含义是nums中小于target的元素有x个
    if(left == nums.size() || nums[left] != target) return -1;
    return left; //其特殊含义是nums中小于target的元素有left个
}

说明：

1. 能搜索左侧边界的关键在于if(nums[mid] == target) right = mid - 1; ，找到target时不要立即返回，而是缩小搜索区间的上界right，在区间[left ，mid - 1]中继续搜索，即不断向左搜索，达到搜索左侧边界的目的
2. left 和 right 的更新 思路 关键在于把握区间的切割，保证切割后的两个区间也是左闭右闭的
3. left的含义是nums中小于target的元素有left个，所以left的取值范围[0， nums.size()]，所以当left == nums.size() 或者nums[left] != target时，表示未找到target，返回-1；否则表示找到，left所指即为答案。

左闭右开区间

int left_bound(vector<int>& nums, int target){
    if(nums.size() == 0) return -1;
    int left = 0, right = nums.size(); //左闭右开区间[left,right)
    while(left < right){ //循环终止条件left == right [right, right)区间为空
        int mid = left + (right - left) / 2;
        if(nums[mid] == target) right = mid; // 注意
        else if(nums[mid] < target) left = mid + 1;
        else if(nums[mid] > target) right = mid; 
    }
    //循环退出的条件是 left == right
    if(left == nums.size() || nums[left] != target) return -1;
    return left;//其特殊含义是nums中小于target的元素有left个
}

说明：

1. 当找到target值时，不要立即返回，缩小区间的上界，在区间[left， mid)中继续搜索，所以更新right = mid

1.4 寻找右侧边界的二分搜索

提供两种写法

左闭右闭区间

int right_bound(vector<int>& nums, int target){
    if(nums.size() == 0) return -1;
    int left = 0, right = nums.size() - 1; //左闭右闭区间
    while(left <= right){
        int mid = left + (right - left) / 2;
   		if(nums[mid] == target) left = mid + 1; //注意
        else if(nums[mid] < target) left = mid + 1;
        else if(nums[mid] > target) right = mid - 1;
    }
    //最后检查right越界情况
    if(right < 0 || nums[right] != target) return -1;
    return right;
}

左闭右开区间

int right_bound(vector<int>& nums, int target){
    if(nums.size() == 0) return -1;
    int left = 0, right = nums.size(); //左闭右开区间
    while(left < right){
		int mid = left + (right - left) / 2;
       	if(nums[mid] == target) left = mid + 1; //注意
        else if(nums[mid] < target) left = mid + 1;
        else if(nums[mid] > target) right = mid;
    }
    //注意：因为对left的更新必须是left = mid + 1，也就是说while循环终止时，nums[left]一定不等于target了，而nums[left - 1]可能等于target
    if(left == 0 || nums[left - 1]) return -1;
    return left - 1;
}

左闭右开区间搜索右侧边界时，需要减1

1.5 二分搜索模板统一(左闭右闭)

对于寻找左右边界的二分搜索，常见的方式是使用左闭右开的搜索区间，为了便于记忆，全部统一为左闭右闭区间

int binarySearch(vector<int>& nums, int target){
    if(nums.size() == 0) return -1;
    int left = 0, right = nums.size() - 1; 
    while(left <= right){ 
        int mid = mid = left + (right - left) / 2;
        if(nums[mid] == traget) return mid;  // 直接返回
        else if(nums[mid] < target) left = mid + 1; 
        else if(nums[mid] > target) right = mid - 1;
    }
    // 直接返回
    return -1;
}

int left_bound(vector<int>& nums, int target){
    if(nums.size() == 0) return -1;
    int left = 0, right = nums.size() - 1; 
    while(left <= right){ 
        int mid = mid = left + (right - left) / 2;
        if(nums[mid] == target) right = mid - 1; // 固定左边界，收缩右边界
        else if(nums[mid] < target) left = mid + 1;
        else if(nums[mid] > target) right = mid - 1;
    }
    // 最后检查left越界的情况 
    if(left == nums.size() || nums[left] != target) return -1;
    
    return left; 
}


int right_bound(vector<int>& nums, int target){
    if(nums.size() == 0) return -1;
    int left = 0, right = nums.size() - 1; 
    while(left <= right){
        int mid = left + (right - left) / 2;
   		if(nums[mid] == target) left = mid + 1; // 固定右边界，收缩左边界
        else if(nums[mid] < target) left = mid + 1;
        else if(nums[mid] > target) right = mid - 1;
    }
    //最后检查right越界情况
    if(right < 0 || nums[right] != target) return -1;
    
    return right;
}

1.6 二分搜索模板统一(左闭右开)

int binarySearch(vector<int>& nums, int target){
    if(nums.size() == 0) return -1;
    int left = 0, right = nums.size(); 
    while(left < right) { 
        int mid = mid = left + (right - left) / 2;
        if(nums[mid] == target) return mid; // 直接返回
        else if(nums[mid] < target) left = mid + 1; 
        else if(nums[mid] > target) right = mid; 
    }
    // 直接返回
    return -1;
}


int left_bound(vector<int>& nums, int target){
    if(nums.size() == 0) return -1;
    int left = 0, right = nums.size(); 
    while(left < right){ 
        int mid = left + (right - left) / 2;
        if(nums[mid] == target) right = mid;  // 固定左边界，收缩右边界
        else if(nums[mid] < target) left = mid + 1;
        else if(nums[mid] > target) right = mid; 
    }
    if(left == nums.size() || nums[left] != target) return -1;
    
    return left;//其特殊含义是nums中小于target的元素有left个
}


int right_bound(vector<int>& nums, int target){
    if(nums.size() == 0) return -1;
    int left = 0, right = nums.size(); //左闭右开区间
    while(left < right){
		int mid = left + (right - left) / 2;
       	if(nums[mid] == target) left = mid + 1; //注意
        else if(nums[mid] < target) left = mid + 1;
        else if(nums[mid] > target) right = mid;
    }
    if(left == 0 || nums[left - 1]) return -1;
    return left - 1; //注意返回的是 left - 1
}