经典面试题(二十三)--二叉树与双向链表
Posted 算法和数据结构
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了经典面试题(二十三)--二叉树与双向链表相关的知识,希望对你有一定的参考价值。
来源:LeetCode
难度:中等
描述:
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点,只能调整树中节点指针的指向。
为了让您更好地理解问题,以下面的二叉搜索树为例
我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表,第一个节点的前驱是最后一个节点,最后一个节点的后继是第一个节点。
下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点。
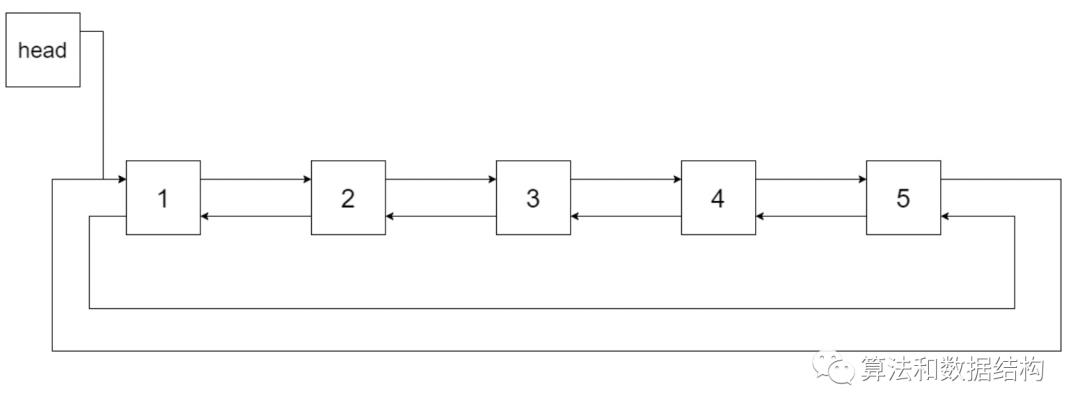
特别地,我们希望可以就地完成转换操作。当转化完成以后,树中节点的左指针需要指向前驱,树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针
分析:
题意给一棵二叉搜索树,让咱们返回一个排序后的循环双向链表。
众所周知,二叉搜索树的特点是整棵树中的每个节点都满足:根节点大于左节点,小于右节点,所以对于一棵二叉搜索树,只要采用中序遍历(左根右)的方式就能得到一个排序好的数组
所以在本题中,咱们只要采用中序遍历的方式遍历二叉搜索树,并将节点间用左右指针的方式串连成双向链表即可。以下介绍两种方法求解
解题
方法一:额外存储法
思路:
采用中序遍历方式遍历二叉搜索树,并将每个节点存储到List数组中,结束后便能得到一个递增排序的数组,最后只要将数组中每个节点串连起来即可
代码:
1public Node<Integer> treeToDoublyList(Node<Integer> root) {
2 if (root == null) {
3 return null;
4 }
5 List<Node<Integer>> list = new ArrayList<>();
6 //中序遍历二叉搜索树
7 midOrder(root, list);
8 //第一个节点最小 作为头结点
9 Node<Integer> head = list.get(0);
10 for (int i = 0; i < list.size() - 1; i++) {
11 //依次串连相邻节点
12 build(list.get(i), list.get(i + 1));
13 }
14 //串连尾节点和头结点
15 build(list.get(list.size() - 1), list.get(0));
16 return head;
17}
18
19private void build(Node<Integer> left, Node<Integer> right) {
20 //上一个节点的 right 指针指向下一个节点
21 left.right = right;
22 //下一个节点的 left 指针指向上一个节点
23 right.left = left;
24}
25
26private void midOrder(Node<Integer> root, List<Node<Integer>> list) {
27 if (root == null) {
28 return;
29 }
30 //中序遍历二叉搜索树,并将每个节点存储到List数组中
31 midOrder(root.left, list);
32 list.add(root);
33 midOrder(root.right, list);
34}
时间复杂度:O(n) n为节点个数
空间复杂度:O(n)
方法二:原树中序遍历法
思路:
同样采用中序遍历的方式遍历二叉搜索树,本次不保存节点,直接在遍历的过程中将节点串连起来。
使用一个变量head来记录第一个节点的指针,再使用一个变量pre来记录遍历当前节点之前遍历的那个节点,主要用它来和当前节点给串起来
代码:
1//记录头结点,用来最后返回的
2private Node head = null;
3//记录遍历的当前节点的前一个节点,
4//用来把当前节点给串起来的
5private Node pre = null;
6
7public Node treeToDoublyList(Node root) {
8 if (root == null)
9 return root;
10 inorder(root);
11 //注意,上面的方法中,我们只是把第一个接点到
12 //最后一个节点串了起来,但并没有把第一个节点
13 //和最后一个节点串起来连成一个环形,所以这里
14 //还要把链表的首尾连接起来(这里pre已经是尾节点了)
15 head.left = pre;
16 pre.right = head;
17 return head;
18}
19
20//二叉树的中序遍历
21private void inorder(Node root) {
22 //边界条件的判断
23 if (root == null)
24 return;
25 //先遍历左子节点
26 inorder(root.left);
27 //下面是对当前节点的操作
28 if (pre == null) {
29 //这行代码只会执行一次,就是root是树的左子节点的
30 //左子节点的……,一直没有左子节点为止,实际上就是中
31 //序遍历结果的第一个节点
32 head = root;
33 } else {
34 //串起来的结果就是前一个节点pre的right指向当前节点,
35 //然后当前节点的left指向前一个节点pre
36 pre.right = root;
37 }
38 root.left = pre;
39 //前一个节点和当前节点串起来之后,就让当前节点变成前一个节点
40 pre = root;
41 //最后在遍历右子节点
42 inorder(root.right);
43}
时间复杂度:O(n) n为节点个数
空间复杂度:O(n)
以上仅是个人思路解法,觉得还不错欢迎点赞关注分享
往期精彩推荐
以上是关于经典面试题(二十三)--二叉树与双向链表的主要内容,如果未能解决你的问题,请参考以下文章