二分查找和快速排序(理论+代码)
Posted 运筹帷幄Q
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了二分查找和快速排序(理论+代码)相关的知识,希望对你有一定的参考价值。
哈喽,大家好,好久不见,甚是想念(虽然上周刚见)。
欢迎关注哔哩哔哩UP主:我家公子Q
上述两种算法速度相对较慢,今天给大家带来的是二分查找和快速排序。难度不大。
1 二分查找
1.1 基本原理
1.2 python代码
2 快速排序
2.1 基本原理
2.2 python代码
2.3 为什么快?

相信很多人小时候都玩过猜字游戏,就是你想一个数,然后让你的小伙伴猜,然后你告诉小伙伴猜大了还是猜小了,这样直至小伙伴猜到那个数字。(没玩过的假装玩过!!!!)

上边其实就是二分查找的最基本的原理。这里还是给出具体的例子,并对比最基本的遍历查找:比如1-100之间随便想一个数字,然后查找出这个数字。然后二分查找的演变过程就如下图所示。
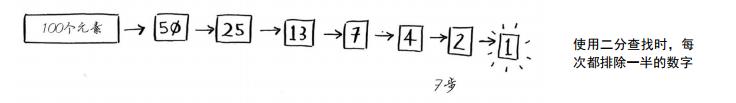
如果简单查找的话,需要遍历每一个元素,其时间复杂度为O(n);而二分查找的时间复杂度则为O(logn)

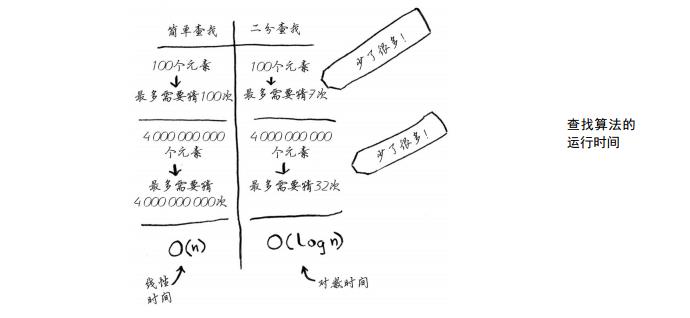
但是你仔细想一想,上边的猜字游戏里面,在判断之前,实际上你有一个排序的过程,排完序以后,通过判断直接去除了不满足条件的那一部分序列,所以二分查找的应用对象是有序的数列,这一点要特别注意!!!

比如这里我们查找的是一个有序数组里面的某一个值,如果在里面就返回其位置,否则返回不在里面。
其实我们是需要根据每次的判断(猜大了还是猜小了,将low或high进行移动的),下面在代码中体会!
# 注意此处输入应为排序后的列表
def binary_find(arr, a):
low = 0
high = len(arr) - 1
while low <= high:
mid = (low + high) // 2 # 猜的数字位置, 如果和不是偶数,则自动将mid向下取整
guess = arr[mid]
if guess == a:
return mid
if guess > a:
high = mid - 1
else:
low = mid + 1
return None
print(binary_find([1, 2, 3, 4, 5, 15, 20], 3))
2
这里有种分而治之(Divide and conquer, D&C)的思想十分重要,使用递归来实现,就是不断将问题规模进行缩小。
举一个最简单的例子,比如说求一个数组的和。(当然任何高级编程语言应该都打包好了求和函数,这里只是为了说明分而治之的递归思想)。
这里应该涉及到栈这种后进先出(Last in first out)的数据结构,可以找资料看一看。 使用分而治之解决问题的过程包括两个步骤:
(1) 找出基线条件,这种条件必须尽可能简单;
(2)不断将问题分解(或者说缩小规模),知道符合基线条件。
现在有一个列表[2, 4, 6, 8],需要求它的和。对于求和,我们最熟悉的(也是最简单的)是两个数相加,那基线条件找到了,就是如果只剩两个数相加;那如何缩小问题规模呢?
分解的过程见下图:
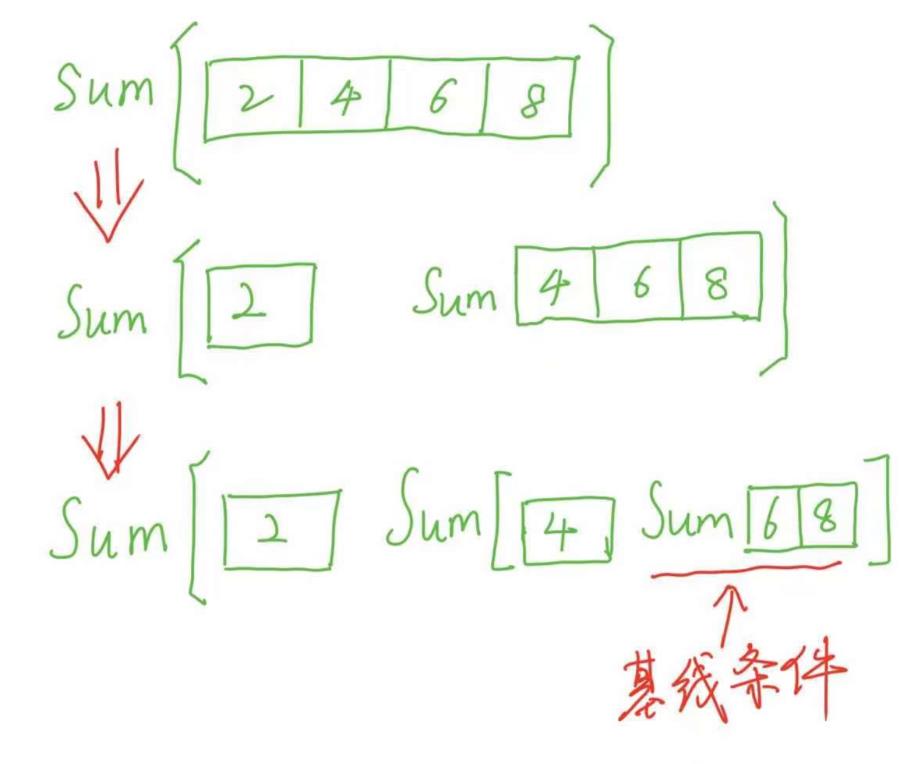
那这个原理写成代码的话,是什么样呢?如下:
def my_sum(arr):
if len(arr) == 2:
return arr[0] + arr[1]
else:
return arr[0] + my_sum(arr[1:])
print(my_sum([1, 2, 3]))
6
OK,理解这以后,我们进一步看一下在排序里面是如何应用的! 还是按照刚才的步骤:
第一步,先找基线条件。最简单的排序应该是一个元素或者没有元素的列表,都不用排序。
第二步,问题分解。当元素个数增加了,怎么处理呢?下面讲述分解的过程。
比如,[1, 8, 5, 6 ],把这个数组进行从小到大的排序。 首先,我们需要找一个元素作为基准值,比如说把5作为基准值,然后把整个数组按照与基准值的大小关系,分开,这个过程称之为分区。
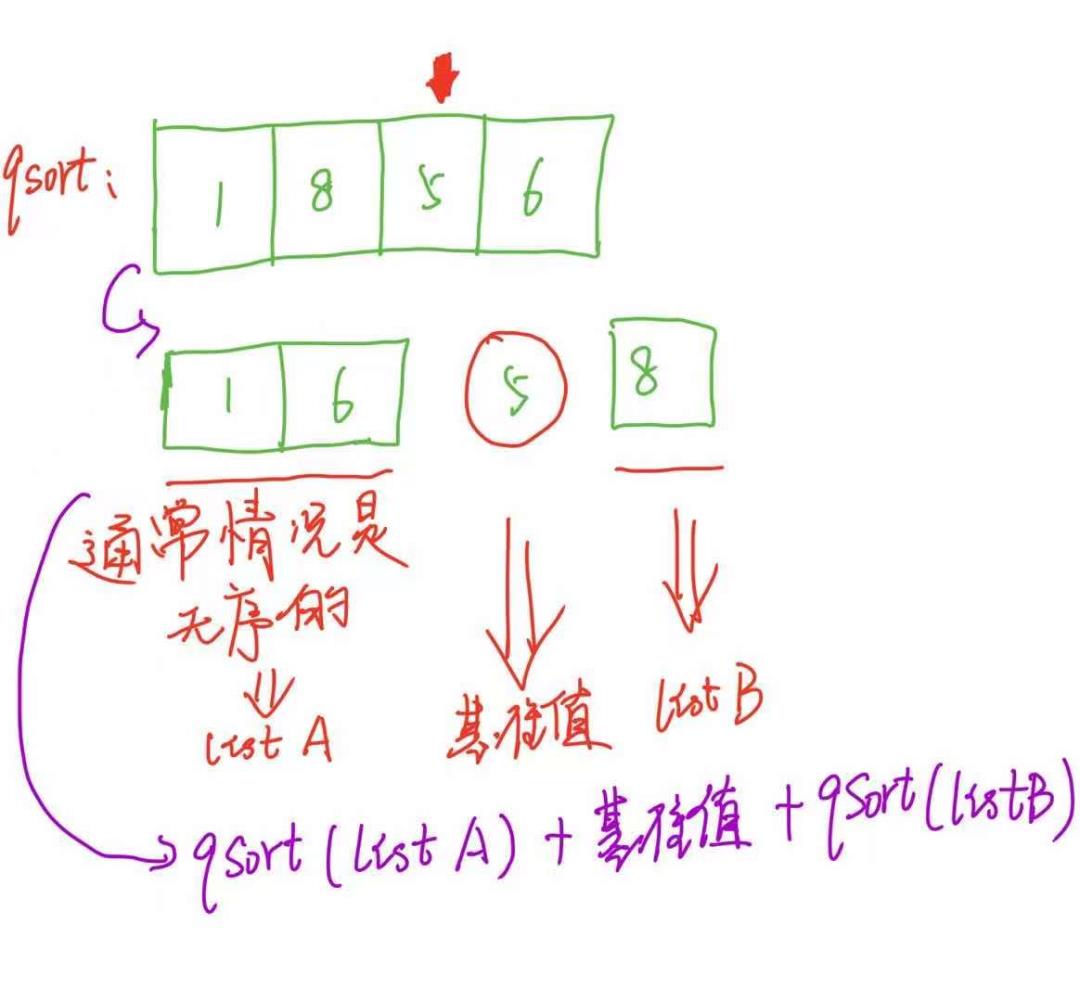
分区之后,基准值两侧的列表通常是无序的,然后继续按照此逻辑将两侧进行分区,排序,就ok了,我们来看下代码。
# 从小到大排列
def quick_sort(arr):
# 基线条件
if len(arr) < 2:
return arr
# 问题分解
else:
mid = arr[0] # 以第一个数为基准值
left = [i for i in arr if i < mid]
right = [i for i in arr if i > mid]
return quick_sort(left) + [mid] + quicksort(right)
print(quick_sort([1, 20, 5, 4, 3, 15, 2]))
[1, 2, 3, 4, 5, 15, 20]怎么样,看明白了嘛? 递归函数在没达到基线条件(终止条件)时,中间对于函数的调用会被挂起,一直到达最后的基线条件之后,再回过头来一步一步运行挂起的函数。 个人感觉,这东西,一看就会,上手就废,总而言之,容易学废! 所以建议一步一步推导几个简单的试试。

这里把它和选择排序作比较,选择排序算法实际上时两层循环,外层是按照顺序依次放置元素,逐步完善已排好的前部分序列,内层循环则是在剩余完成排序的序列中找到最小值(若从大到小则是最大值),选择排序算法的时间复杂度是O(n2);那么快速排序呢?
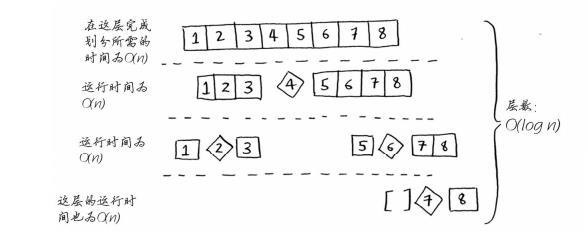
快速排序算法的最佳运行时间为O(n logn),这里要告诉你的是,最佳情况也是平均情况。只要你每次都随机地选择一个数组元素作为基准值,快速排序的平均运行时间就将为O(n log n)。(实际上快速算法在最糟糕的情况下的,运行时间为O(n2))

参考文献:[美]Aditya Bhargava(著),袁国忠(译). 《算法图解》.人民邮电出版社,2017.3
▼

以上是关于二分查找和快速排序(理论+代码)的主要内容,如果未能解决你的问题,请参考以下文章