Cesium中用到的图形技术——Horizon Culling

Posted 2021-08-12 人生海海 山山而川

详细介绍了Cesium中用到的地平线裁剪的技术。

译者注：本文翻译自Cesium官方博文《Horizon Culling》，by KEVIN RING。

目录

• 地平线针对球体剔除一个点
• 平面测试
• 圆锥测试
• 推广到椭球
• 代码
• 预览

在开发像Cesium这样的虚拟数字地球时，我们需要能够快速确定场景中的对象（例如地形图块，卫星，建筑物，车辆等）何时不可见，因此不需要渲染。当然，我们进行视锥体裁剪。但是，另一种重要的剔除类型是地平线剔除。

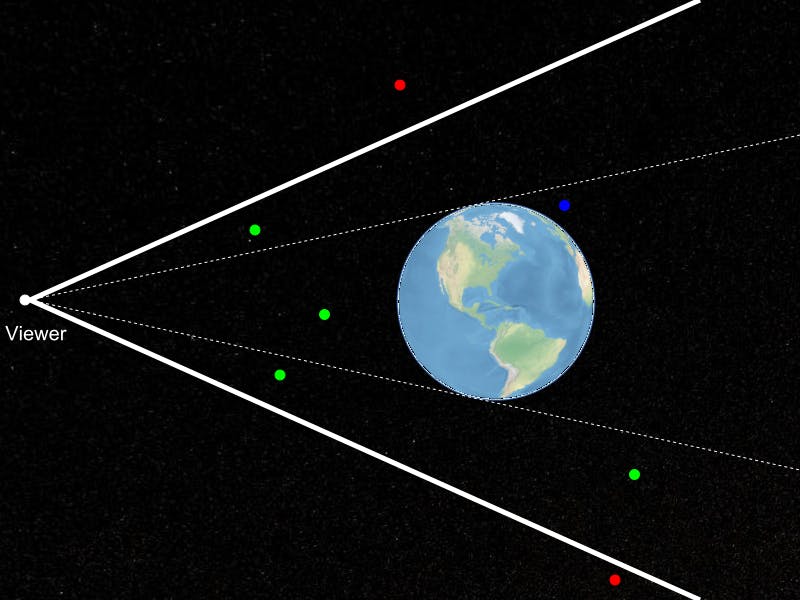
在上图中，观看者可以看到绿点。 红点不可见，因为它们在视锥面之外，用粗白线表示。 蓝点位于视锥中，但由于地球遮挡住，因此观看者看不到。 换句话说，它在地平线之下。 “地平线剔除”是一个简单的想法，您无需渲染从当前查看器位置观察到的位于地平线以下的对象。 听起来很简单，但细节变得棘手，特别是因为它需要非常快。 Cesium会对每个渲染帧进行数百次此测试，以测试地形图块的可见性。 不过，这是一项重要的测试。 在上图中的配置中，覆盖整个地球的地形图块位于视锥中。 但是，其中有一半以上不在地平线范围内，不需要渲染。

几年前，Deron Ohlarik写了两篇有关地平线剔除的出色文章。 此后，我们对他的技术进行了扩展，我想在这里分享。 尽管它仅适用于地形图之类的静态数据，但我们发现它非常有用，因为它比以前的技术更快，更准确。 精度的提高来自对地球的椭球模型的视界剔除，而不是球面近似。

我首先要提到，这项技术的功劳完全归功于我的同事弗兰克·斯通纳（Frank Stoner）。 我所做的唯一贡献就是在他做了艰辛的工作后，在Cesium中实现了它，并在此处进行了编写。

地平线针对球体剔除一个点

如Ohlarik所述，出于水平剔除的目的，我们可以为静态对象（例如地形图块）计算边界球，该边界球是如此紧密以至于它仅仅是一个点。 如果该点在地平线以下，那么我们可以确保整个图块也在地平线以下。 我们的新技术仅限于针对椭球体选出一个点，因此我们假设此“遮挡点”已被计算出来。 有关如何完成此操作的详细信息，请参见后续博客文章。

我保证我们会针对普通的椭球体实施视界剔除，而我会兑现这一诺言，但让我们首先使用一个简单的单位球体进行视界剔除。 然后，我将证明我们可以轻松地将其概括为任意的椭球体。 考虑下图：

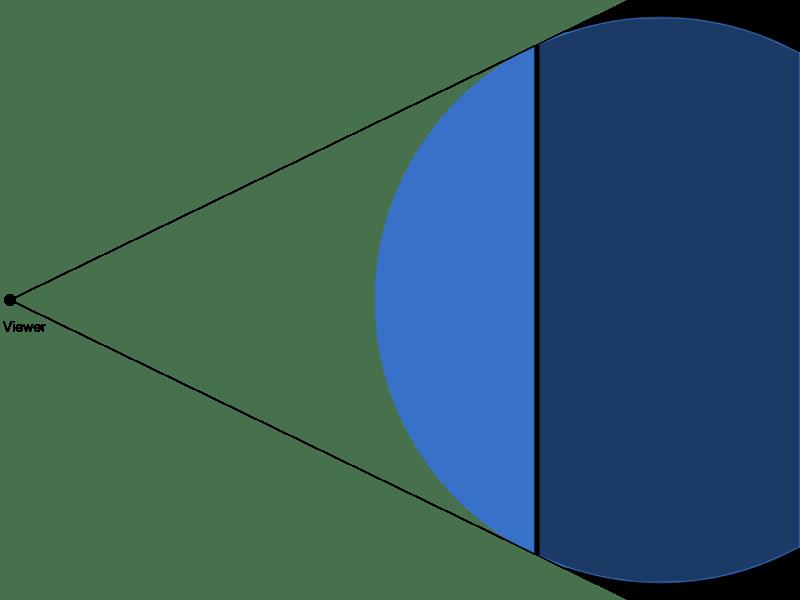
在此图中，蓝色圆圈是我们的单位球面。 从摄影机位置延伸并与球体相切的线代表地平线。黑色垂直线代表所有地平线点。在我们的单位球面上，地平线点位于平面上并形成一个圆。从摄像机位置到所有地平线点的向量形成一个无限锥。

球体的部分及其周围的空间以灰色阴影表示代表地平线以下的区域。从摄像机位置看不到阴影区域中的任何点。直观地说，如果该点位于由切向量形成的无限锥内，则该点位于地平线下方，并且位于包含所有地平线点的平面之后。

平面测试

首先，让我们进行一项代价很小的测试，以确定一个点在平面的哪一侧。 考虑下图：

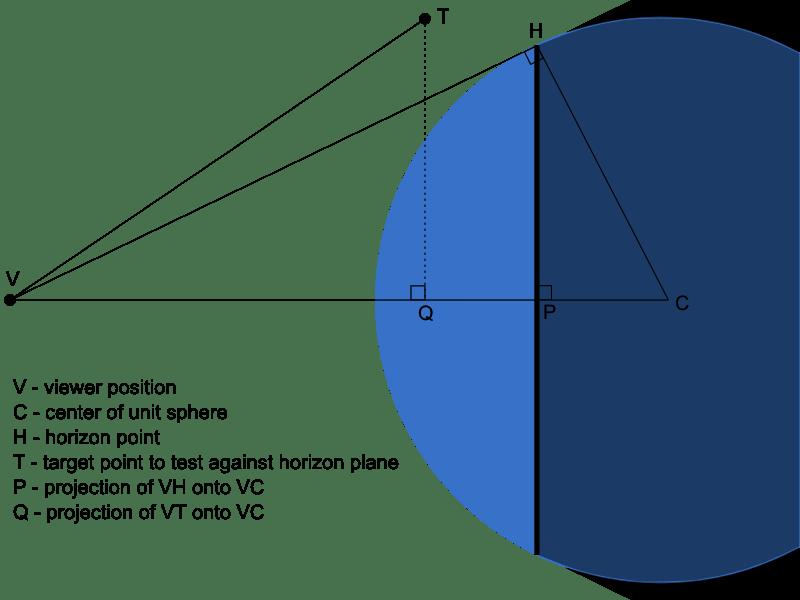
我们知道向量\\(\\vec{VC}\\)和\\(\\vec{VH}\\)分别是相点到目标点和相点到椭球中心点的向量。同时，由于这里使用的是单位球，向量\\(\\vec{HC}\\)是一个单位向量，根据勾股定理：

\\[\\lVert \\vec{VH} \\rVert^2 + \\lVert \\vec{HC} \\rVert^2 = \\lVert \\vec{VC} \\rVert^2 \\]

\\[\\lVert \\vec{VH} \\rVert^2 = \\lVert \\vec{VC} \\rVert^2 - 1 \\]

接下来，我们注意到三角形△VCH和△HCP是相似三角形。他们共享一个位于C点的角并且都有一个直角，因此：

\\[\\frac{\\lVert \\vec{PC} \\rVert}{\\lVert \\vec{HC} \\rVert} = \\frac{\\lVert \\vec{HC} \\rVert}{\\lVert \\vec{VC} \\rVert} \\]

\\[\\frac{\\lVert \\vec{PC} \\rVert}{1} = \\frac{1}{\\lVert \\vec{VC} \\rVert} \\]

\\[\\lVert \\vec{PC} \\rVert = \\frac{1}{\\lVert \\vec{VC} \\rVert} \\]

因此，从视点到平面的距离为：

\\[\\lVert \\vec{VP} \\rVert = \\lVert \\vec{VC} \\rVert - \\frac{1}{\\lVert \\vec{VC} \\rVert} \\]

如果\\(\\vec{VT}\\)在\\(\\vec{VC}\\)上的投影小于\\(\\lVert \\vec{VP} \\rVert\\)，那么目标点就在平面之前。换句话说，目标点在视平面之后的条件是：

\\[\\vec{VT} \\cdot \\hat{VC} > \\lVert \\vec{VC} \\rVert - \\frac{1} {\\lVert \\vec{VC} \\rVert} \\]

两边同时乘以\\(\\lvert \\vec{VC} \\rvert\\):

\\[\\vec{VT} \\cdot \\vec{VC} > \\lVert \\vec{VC} \\rVert ^ 2 - 1 \\]

综上所述，要确定目标点是否在视线平面之后，可以使用视点到目标点的矢量，与视点到椭球体的中心的矢量的点积。 如果该值大于从观察者到椭球中心的向量的模的平方减一，则目标点在平面后面。不需要开平方或三角函数操作。

圆锥测试

如果目标点在视平面前面，那么该目标点绝对不会被球体遮挡，此时工作就完成了。但是，如果它在视平面后方，能否被遮挡是不确定的。如果目标点也在，视点与所有地平线点连接而形成的无限锥体内，则它被遮挡。如果它在那个圆锥体之外，那么它不会被遮挡。那么我们如何通过圆锥测试点呢？

让我们再次看一下图，这次是角度∠HVC标记为α，∠TVC标记为β：

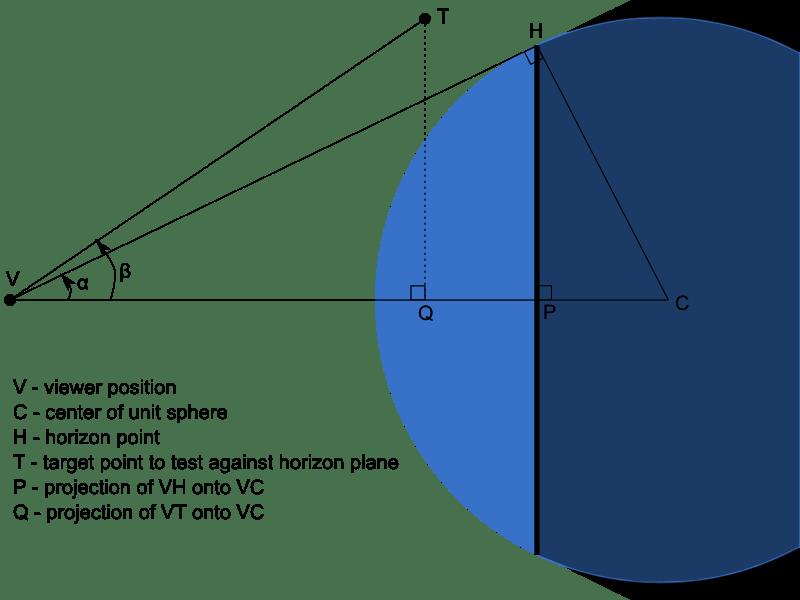
可以看到，如果点T要在圆锥体内，那么：

\\[β < α \\]

对于\\(0<=θ<=π\\)，有：

\\[cos(β) > cos(α) \\]

角α是直角三角形△VCH的一部分，所以我们通过三角函数，重写不等式的右边：

\\[cos(β) > \\frac{\\lVert \\vec{VH} \\rVert}{\\lVert \\vec{VC} \\rVert} \\]

根据点积的定义，有：

\\[{\\vec{VT}} \\cdot {\\vec{VC}} = {\\lVert \\vec{VT} \\rVert} {\\lVert \\vec{VC} \\rVert} {cos(β)} \\]

\\[cos(β) = \\frac {{\\vec{VT}} \\cdot {\\vec{VC}}} {{\\lVert \\vec{VT} \\rVert} {\\lVert \\vec{VC} \\rVert} } \\]

\\[\\frac {{\\vec{VT}} \\cdot {\\vec{VC}}} {{\\lVert \\vec{VT} \\rVert} {\\lVert \\vec{VC} \\rVert} } > \\frac{\\lVert \\vec{VH} \\rVert}{\\lVert \\vec{VC} \\rVert} \\]

\\[\\frac {{\\vec{VT}} \\cdot {\\vec{VC}}} {\\lVert \\vec{VT} \\rVert} >\\lVert \\vec{VH} \\rVert \\]

为了求平方根的操作，两边都进行平方：

\\[\\frac {({\\vec{VT}} \\cdot {\\vec{VC}})^2} {\\lVert \\vec{VT} \\rVert^2} >\\lVert \\vec{VH} \\rVert^2 \\]

通过对两边进行平方，针对对顶圆锥，我们能有效地测试目标点，其中第二个锥体从观察者指向远离椭圆体。然而，这不会影响我们的结果，因为观察者后面的目标点肯定在地平线前面。视平面前面的任何点都不能被地平线剔除，因此不需要第二个锥体测试。

现在我们站在哪里？\\(\\vec{VC}\\)和\\(\\vec{VT}\\)很容易从我们已知的椭球中心、目标点和观察者位置计算出来。\\(\\vec{VH}\\)不是那么明显。但是还记得在对视平面进行测试的部分吗？我们发现：

\\[\\lVert \\vec{VH} \\rVert^2 = \\lVert \\vec{VC} \\rVert^2 - 1 \\]

这不仅容易计算，而且我们在确定点在平面的哪一侧的过程中已经这样做了。类似地，我们已经计算了\\(\\vec{VT}\\cdot\\vec{VC}\\)。

所以我们最终的不等式，只需要一点更多的算术运算来评估，如下所示：

\\[\\frac {({\\vec{VT}} \\cdot {\\vec{VC}})^2} {\\lVert \\vec{VT} \\rVert^2} >\\lVert \\vec{VC} \\rVert^2 - 1 \\]

如果此不等式成立，则目标点在锥体内部。如果它也在地平线后面，则目标点被遮挡。

推广到椭球

在我们漂亮的小单位球世界中，这一切都非常优雅。 我们如何将其推广到任意椭球体？我们的单位球面方程为：

\\[x^2 + y^2 + z^2 = 1 \\]

而椭球的方程为：

\\[\\frac{x^2}{a^2} + \\frac{y^2}{b^2} + \\frac{z^2}{c^2} = 1 \\]

其中a，b和c分别是椭圆体沿x，y和z轴的半径。

给定一个以原点为中心的椭球、一个观察者位置和一个目标位置，我们可以对所有坐标应用缩放变换，以创建一个等效的问题，其中椭球实际上是一个单位球体。 执行缩放操作的矩阵如下所示：

\\[\\left( \\begin{matrix} \\frac{1}{a} & 0 & 0\\\\ 0 & \\frac{1}{b} & 0 \\\\ 0 & 0 & \\frac{1}{c} \\end{matrix} \\right) \\]

我们将此缩放坐标系称为椭球缩放空间，并发现它对于解决椭球上的各种问题很有用。
可以在SIGGRAPH 2010上展示的海报GPU Ray Casting of Virtual Globes的第2节中找到对该主题的更严密的处理。

代码

我认为把所有的数学都写出来很重要，但这一切都归结为一些简单的代码。每次相机位置改变时，我们执行：

// Ellipsoid radii - WGS84 shown here
var rX = 6378137.0;
var rY = 6378137.0;
var rZ = 6356752.3142451793;

// Vector CV
var cvX = cameraPosition.x / rX;
var cvY = cameraPosition.y / rY;
var cvZ = cameraPosition.z / rZ;

var vhMagnitudeSquared = cvX * cvX + cvY * cvY + cvZ * cvZ - 1.0;

然后，对于我们希望测试遮挡剔除的每个点：

// Target position, transformed to scaled space
var tX = position.x / rX;
var tY = position.y / rY;
var tZ = position.z / rZ;

// Vector VT
var vtX = tX - cvX;
var vtY = tY - cvY;
var vtZ = tZ - cvZ;
var vtMagnitudeSquared = vtX * vtX + vtY * vtY + vtZ * vtZ;

// VT dot VC is the inverse of VT dot CV
var vtDotVc = -(vtX * cvX + vtY * cvY + vtZ * cvZ);

var isOccluded = vtDotVc > vhMagnitudeSquared &&
                 vtDotVc * vtDotVc / vtMagnitudeSquared > vhMagnitudeSquared;

在 Cesium 中，我们预先计算缩放空间位置，而不是在每次测试之前进行，如上所示。

预览

使用这种技术在Cesium中进行地形剔除，与我们之前使用最小半径边界球剔除的技术相比，我们可以避免绘制大约15%的瓦片，否则我们会在普通场景中绘制。令人高兴的是，新测试对每个图块的执行速度也更快！

到目前为止，我们绕过的一个细节是我们如何从我们的地形图块和其他静态几何体生成“被遮挡物”测试点。目前，我们正在根据（错误但保守的）假设计算每个瓦片的被遮挡点，即使用由椭圆体的最小半径形成的球体来执行遮挡。通过对被遮挡点使用更准确的计算，我们应该能够剔除更多的图块。

更新：这在后续文章中有更详细的介绍。

然而，虽然椭球是用于地平线剔除的方便且相当准确的表面，但我们必须始终牢记，真实地形通常位于椭球下方。如果我们改进被遮挡点的计算，我们必须注意，相对于椭球更准确的地平线剔除最终不会剔除相对于真实地形实际上仍然可见的瓦片。在渲染水下地形时，这尤其可能成为一个问题。