数学建模暑期集训3：排队论

Posted 2021-08-04 Z|Star

文章目录

• 1. 排队系统基本组成
• 2. 排队模型数量指标
• 3. 排队论模型
• • 3.1 单服务台模型
  • • 3.1.1 标准型：M/M/1/ ∞ /∞
    • 3.1.2 系统容量有限型：M/M/1/N/ ∞
    • 3.1.3 顾客源有限型 ：M/M/1/ ∞ /m
    • 3.1.4 例题
  • 3.2 多服务台模型
  • • 3.2.1 标准型：M/M/c
    • 3.2.2 系统容量有限型：M/M/c/N/ ∞
    • 3.2.3 顾客源有限型 ：M/M/c/ ∞ /m
    • 3.2.4 例题
    • 3.2.5 例题2

1. 排队系统基本组成

1.输入过程——顾客到达规律
2.排队规则——顾客按照一定规则排队等待服务
3.服务机构——服务机构的设置，服务台的数量，服务的方式，服务时间分布等

2. 排队模型数量指标

3. 排队论模型

3.1 单服务台模型

设系统输入过程服从泊松流，服务时间服从负指数分布:

3.1.1 标准型：M/M/1/ ∞ /∞

M：输入过程服从泊松流
M：服务时间服从负指数分布
1：1个服务台
∞：顾客源无限
∞：服务台容量无限
服务规则：先到先服务

稳态概率方程：

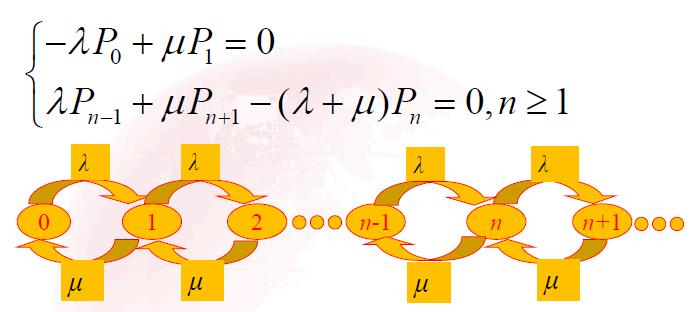
通过上图比较好理解：如同KCL，流入=流出

相应指标：

3.1.2 系统容量有限型：M/M/1/N/ ∞

稳态概率方程：

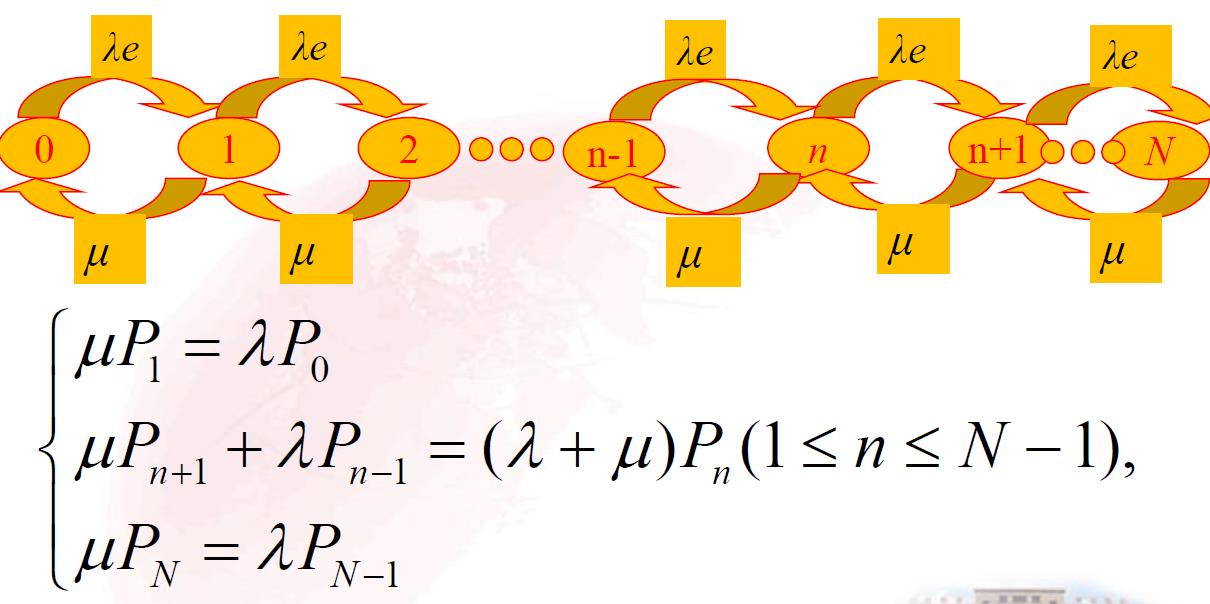
3.1.3 顾客源有限型 ：M/M/1/ ∞ /m

由于顾客源有限，所以该模型与M/M/1/ m /m等价

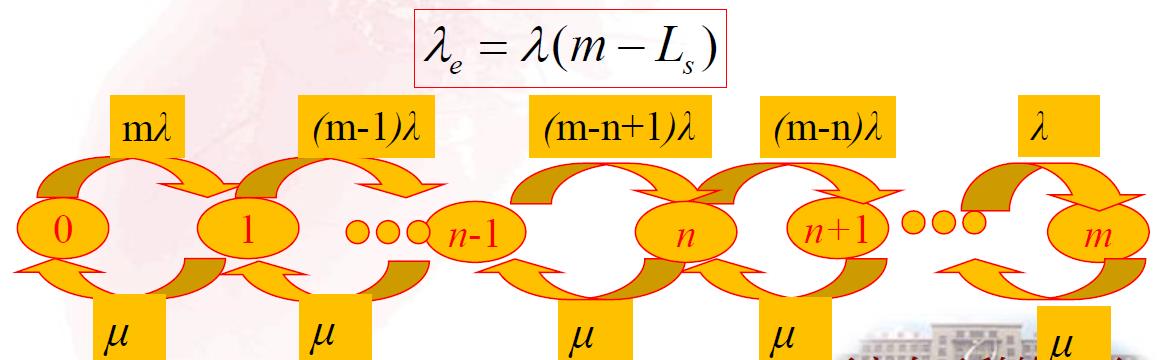
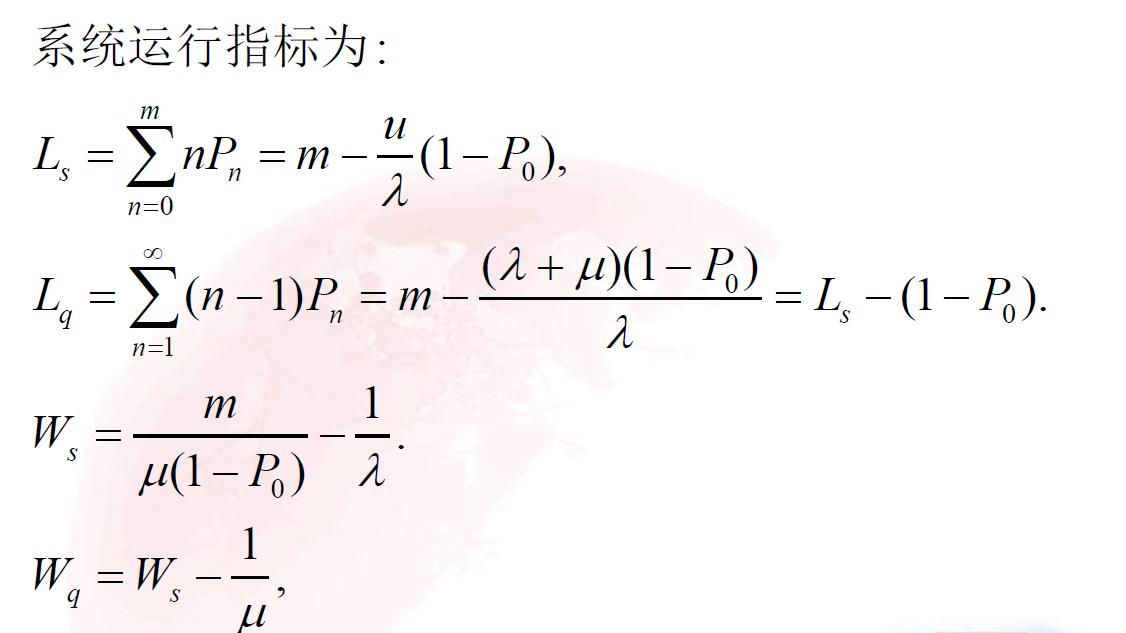
3.1.4 例题

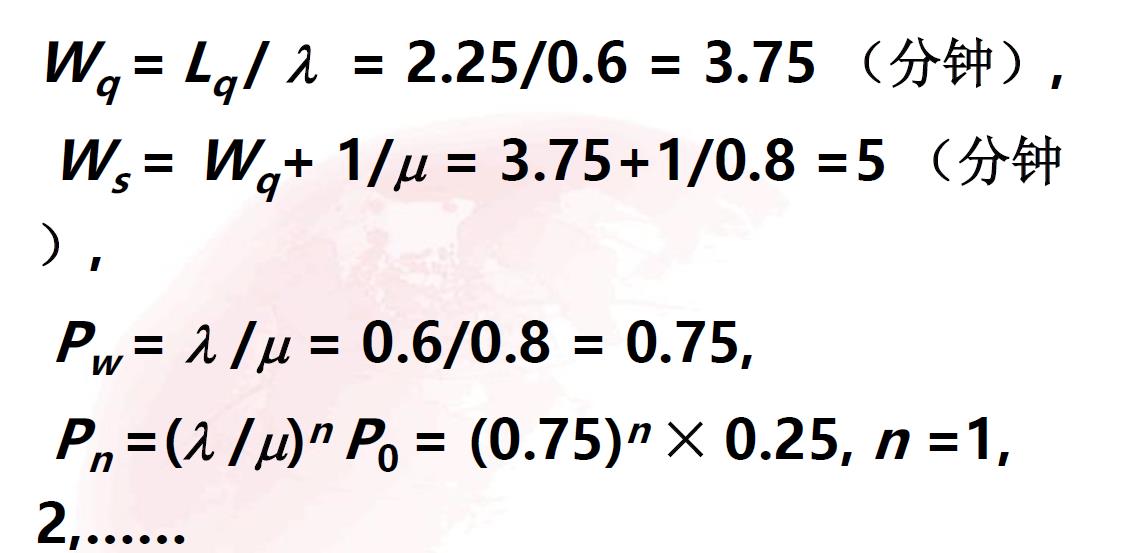
3.2 多服务台模型

3.2.1 标准型：M/M/c

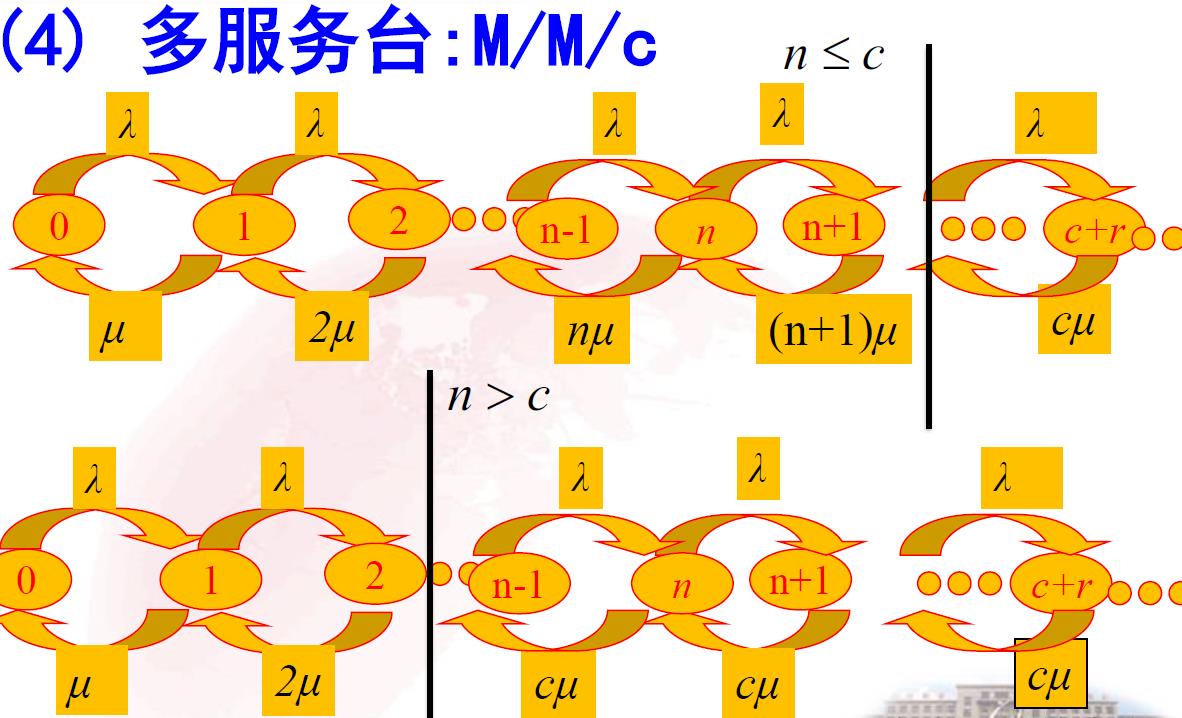
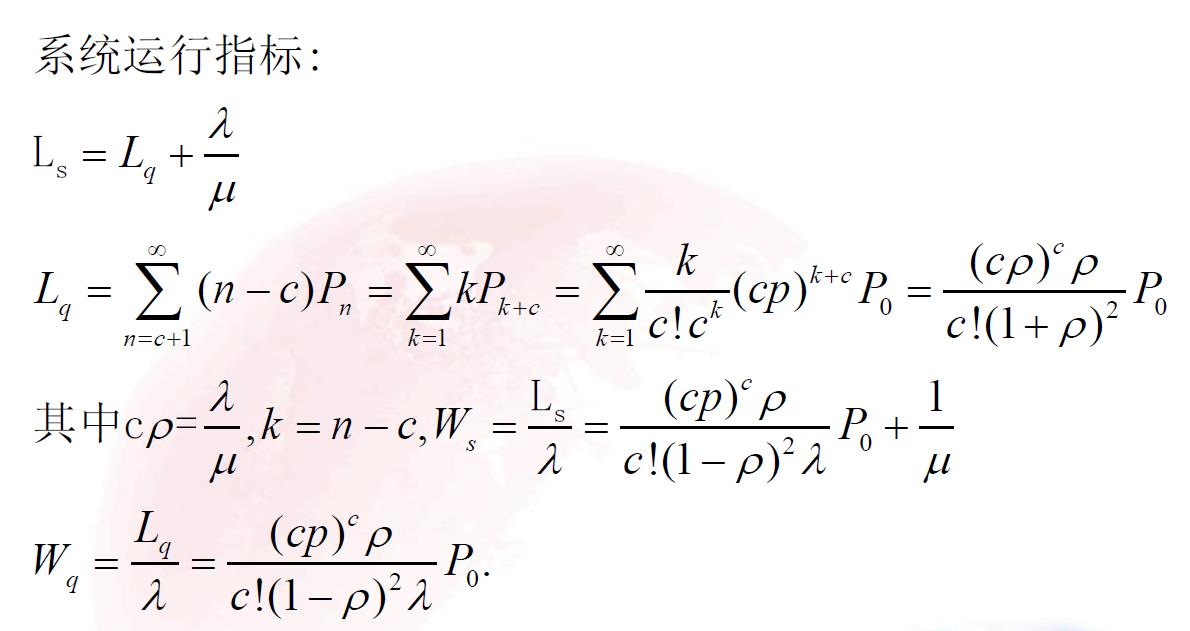
3.2.2 系统容量有限型：M/M/c/N/ ∞

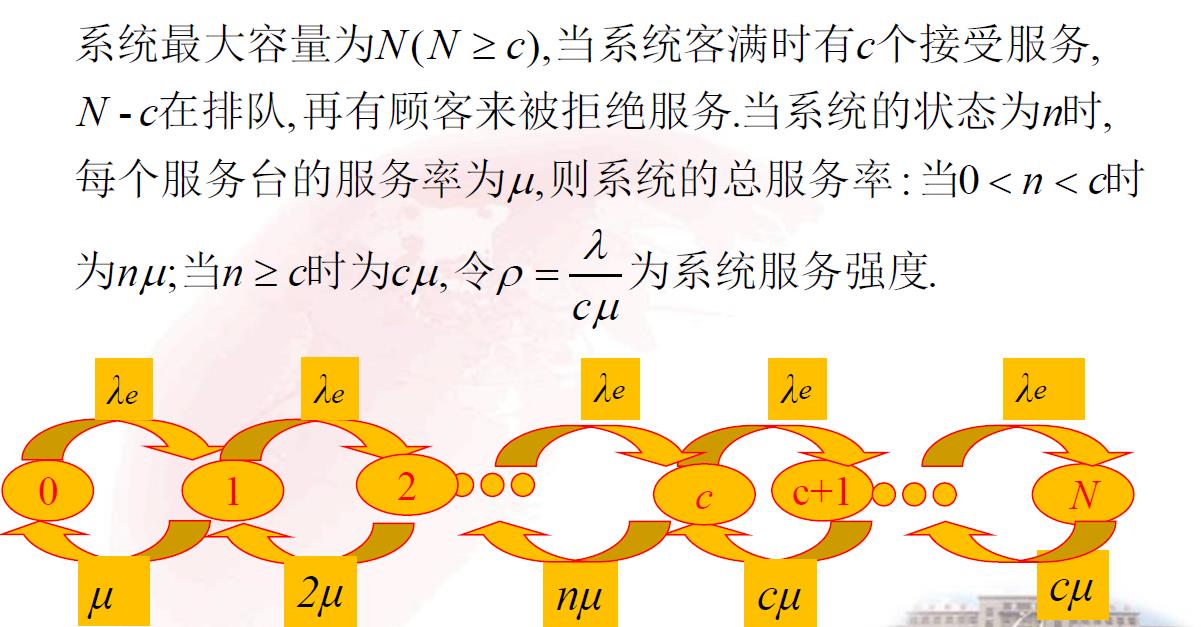
3.2.3 顾客源有限型 ：M/M/c/ ∞ /m

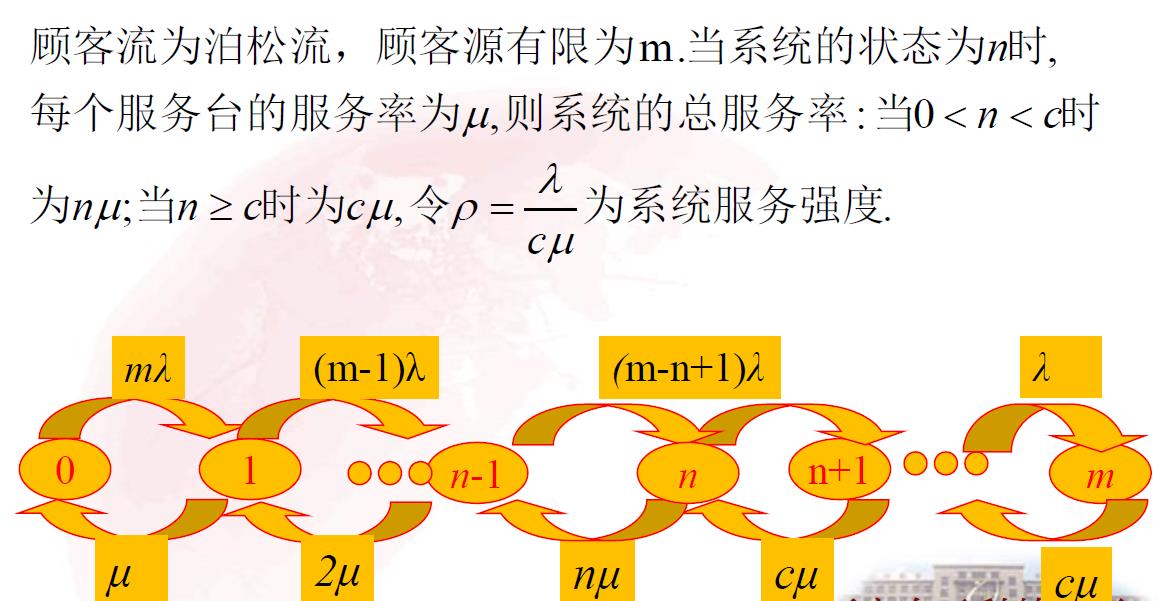
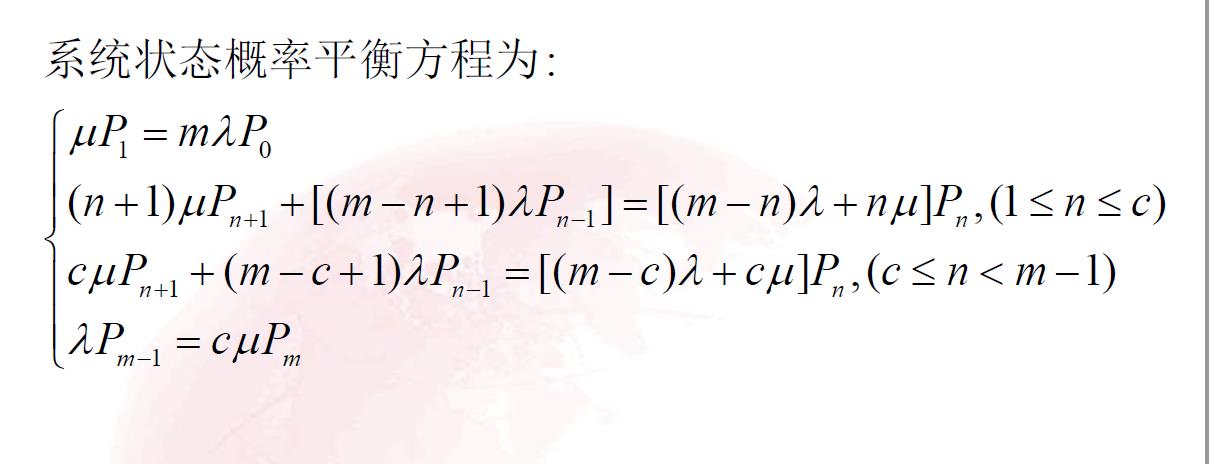
3.2.4 例题

3.2.5 例题2