《LeetCode之每日一题》:85.杨辉三角 II

Posted 2021-08-04 是七喜呀！

杨辉三角 II

• 有关题目
• • 题解

题目链接： 杨辉三角 II

有关题目

给定一个非负索引 k，其中 k ≤ 33，返回杨辉三角的第 k 行。

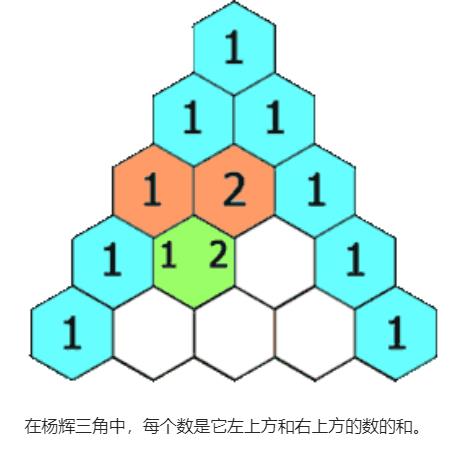
示例:

输入: 3
输出: [1,3,3,1]

题解

法一：递推
代码一：

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int* getRow(int rowIndex, int* returnSize){
    *returnSize = rowIndex + 1;
    int* a[rowIndex + 1];//开辟数组指针
    for (int i = 0; i <= rowIndex; i++){
        a[i] = (int*)malloc((i + 1) * sizeof(int));//不需要int* a[i],上面我们已经定义了
        a[i][0] = a[i][i] = 1;
        for (int j = 1; j < i; j++){
            a[i][j] = a[i - 1][j - 1] + a[i - 1][j];
        }
    }
    return a[rowIndex];
}

代码二：滚动数组

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int* getRow(int rowIndex, int* returnSize){
    *returnSize = rowIndex + 1;
    int* pre = malloc(sizeof(int) * (*returnSize));//记录前一行的数据
    memset(pre, 0, sizeof(int) * (*returnSize));//数据置零
    int* cur = malloc(sizeof(int) * (*returnSize));//当前行的数据
    memset(cur,0,sizeof(int) * (*returnSize));
    for (int i = 0; i <= rowIndex; ++i){
        cur[0] = cur[i] = 1;
        for (int j = 1; j < i; ++j){
            cur[j] = pre[j - 1] + pre[j];
        }
        int* tmp = pre;
        pre = cur;
        cur = tmp;
    }
    return pre;//注意在上面的数据交换中，pre拿到的是当前的数据,即 pre = cur;
}

代码三：滚动数组优化

思路：
我们可以倒着计算当前行，这样计算到第 i 项时，第 i−1 项仍然是上一行的值。（注：你可以从第一行的数据自己推一下看一下）
根据组合数(n,m) = (n - 1, m ) + (n - 1, m - 1)

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int* getRow(int rowIndex, int* returnSize){
    *returnSize = rowIndex + 1;
    int* row = malloc(sizeof(int) * (*returnSize));
    memset(row, 0, sizeof(int) * (*returnSize));
    row[0] = 1;
    for (int i = 0; i <= rowIndex; ++i){
        for (int j = i; j > 0; --j){
            row[j] += row[j - 1];
        }
    }
    return row;//在倒推的过程中，从上往下遍历，主对角线以上的部分全为0，所以row[(*returnSize)] = 1;
}

法二：线性递推

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int* getRow(int rowIndex, int* returnSize){
    *returnSize = rowIndex + 1;
    int* row = (int*)malloc(sizeof(int) * (*returnSize));
    row[0] = 1;
    for (int i = 1; i <= rowIndex; ++i){
        row[i] = 1LL * row[i - 1] * (rowIndex - i + 1) / i;//LL其实代表long long int,这边使用，防止int溢出
        //1LL也就是长长整型的1。
    }
    return row;
}