二叉树--翻转二叉树

Posted 2021-08-04 算法和数据结构

来源：LeetCode

难度：简单

描述：

        翻转一棵二叉树。

示例1：

输入：

输出：

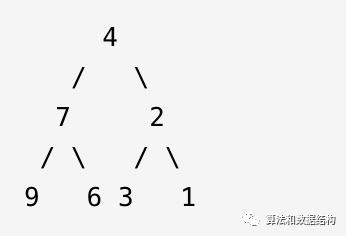
分析：

        题意很清晰，字面上是让咱们将二叉树按根节点做中心线，左右翻转。其实就是将二叉树的每个节点的左右子节点进行交换即可，这里照常介绍深度和广度两种方法，具体思路步骤如下

题外话：二叉树和图类型的题基本考察的都可以利用深度优先遍历（递归、栈）和广度优先遍历（迭代、队列）的方式来做

解题

方法一：深度优先遍历（递归&栈）

思路：如分析，从上至下，交换每个节点的左右节点。

• 终止条件：当前节点为 null 时返回

• 交换完当前节点的左右节点后，再递归的交换当前节点的左节点，之后再交换当前节点的右节点

代码：

 1public TreeNode invertTree(TreeNode root) {
 2    invert(root);
 3    return root;
 4}
 5private void invert(TreeNode root) {
 6    //节点为空  终止
 7    if (root == null) {
 8        return;
 9    }
10    //交换当前节点的左右节点
11    TreeNode tempLeft = root.left;
12    root.left = root.right;
13    root.right = tempLeft;
14    //递归交换左节点
15    invert(root.left);
16    //左节点全部交换完毕后递归交换右节点
17    invert(root.right);
18}

时间复杂度：O(n) n是节点个数

空间复杂度：O(n) 

方法一：广度优先遍历（迭代&队列）

思路：和深度优先遍历一竿子插到底、不行了再退回来继续尝试别的路子的特点不同的是，广度优先遍历的特点是层层扫荡，将本层的元素全部处理完再处理下一层

        广度处理过程：先将根节点放入到队列中，然后不断的迭代队列中的元素。对当前元素调换其左右子树的位置，然后：

• 判断其左子树是否为空，不为空就放入队列中

• 判断其右子树是否为空，不为空就放入队列中

• 之后对队列的元素重复如上操作即可

代码：

 1public TreeNode invertTree(TreeNode root) {
 2    if(root==null) {
 3        return null;
 4    }
 5    //将二叉树中的节点逐层放入队列中，再迭代处理队列中的元素
 6    LinkedList<TreeNode> queue = new LinkedList<TreeNode>();
 7    queue.add(root);
 8    while(!queue.isEmpty()) {
 9        //每次都从队列中拿一个节点，并交换这个节点的左右子树
10        TreeNode tmp = queue.poll();
11        TreeNode left = tmp.left;
12        tmp.left = tmp.right;
13        tmp.right = left;
14        //如果当前节点的左子树不为空，则放入队列等待后续处理
15        if(tmp.left!=null) {
16            queue.add(tmp.left);
17        }
18        //如果当前节点的右子树不为空，则放入队列等待后续处理
19        if(tmp.right!=null) {
20            queue.add(tmp.right);
21        }
22    }
23    //返回处理完的根节点
24    return root;
25}

时间复杂度：O(n) n是节点个数

空间复杂度：O(n) 

以上仅是个人思路解法，觉得还不错欢迎点赞关注分享

往期精彩推荐

• 
  

• 
  

• 
  

扫描下方二维码，关注公众号，更多精彩等你发现