[信息论与编码理论专题-2]：信息与熵

Posted 2021-08-03 文火冰糖的硅基工坊

作者主页(文火冰糖的硅基工坊)：https://blog.csdn.net/HiWangWenBing

本文网址：https://blog.csdn.net/HiWangWenBing/article/details/118526747

---

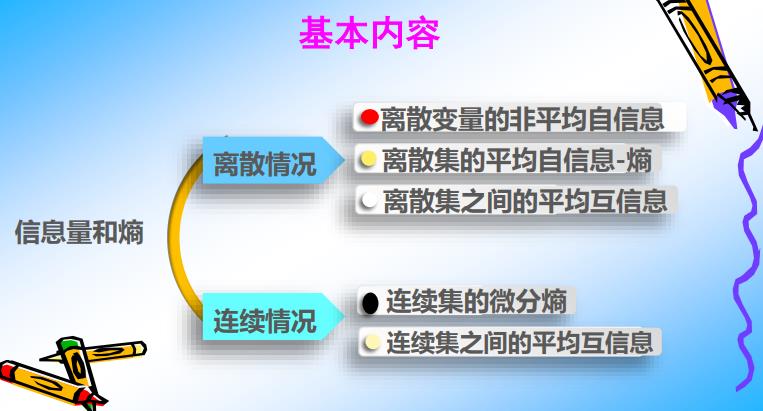
前言：什么是熵

熵的概念是由德国物理学家克劳修斯于1865年所提出。最初是用来描述“能量退化”的物质状态参数之一，在热力学中有广泛的应用。但那时熵仅仅是一个可以通过热量改变来测定的物理量，其本质仍没有很好的解释，直到统计物理、信息论等一系列科学理论发展，熵的本质才逐渐被解释清楚，即，熵的本质是一个系统“内在的混乱程度”。

它在控制论、概率论、数论、天体物理、生命科学等领域都有重要应用，在不同的学科中也有引申出的更为具体的定义，按照数理思维从本质上说，这些具体的引申定义都是相互统一的，熵在这些领域都是十分重要的参量。

低熵，就是高概率，近乎确定性、不费脑子，高关联决定论、高因果联系，低噪度，散点差集中度高，低成本，就是强弱差别明显，就是道德制度法律执行有效，交易成本低，有效率。

高熵，就是低概率，不确定性，费脑子，不确定低关联，低因果关系，高噪度，散点分布厉害，高成本，就是强弱差别不明显，就是道德制度法律执行无效，交易成本高，无效率。

熵增定律是克劳修斯提出的热力学定律，克劳修斯引入了熵的概念来描述这种不可逆过程，即热量从高温物体流向低温物体是不可逆的，其物理表达式为：S =∫dQ/T或ds = dQ/T。

孤立系统总是趋向于熵增，最终达到熵的最大状态，也就是系统的最混乱无序状态。

但是，对开放系统而言，由于它可以将内部能量交换产生的熵增，通过环境向系统增加能量的方式维持系统原有的熵值，所以开放系统有可能趋向熵减而达到有序状态。但这需要外部能量的支撑，当没有外部能量的时候，熵减或熵不变的有序系统就会转向熵增的无序系统。

所谓无序：就是组成每个系统的元素发生的概率是随机的，不确定性的，信息量越大。

越是有序，说明事物的状态越是确定的，事物的状态越是有序的、确定性的，说明事物的信息量越少。

熵与概率：

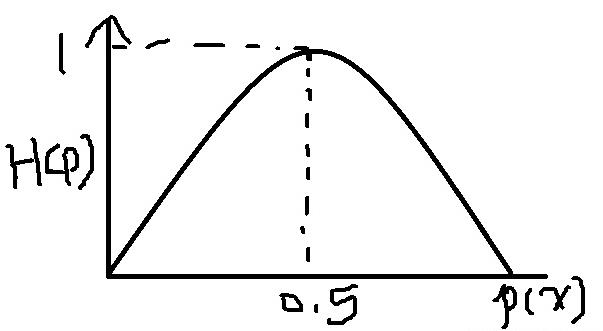
一件事件，发生的概率越大（确定性的发生）或越小（确定性的不发生），则熵值越小。

当一件事件发生的概率为0.5时，表明该事件的发送与不发生是等概率的，表明事件的发生是随机的 ，则此时该事件的熵是最大的。

第1部分  离散变量的非平均自信息

第2部分  离散集的非平均自信息

第3部分  离散集的非平均自信息

第4部分  离散集的非平均互信息

第5部分  连续随机变量的微分熵

第6部分  连续随机变量的互信息

---

附录

作者主页(文火冰糖的硅基工坊)：https://blog.csdn.net/HiWangWenBing

本文网址：https://blog.csdn.net/HiWangWenBing/article/details/118526747

---