模拟退火入门——求解TSP和洛谷P2210
Posted hans774882968
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了模拟退火入门——求解TSP和洛谷P2210相关的知识,希望对你有一定的参考价值。
模拟退火相关介绍:略。这些资料实在太多了,网上大多是拾人牙慧,就懒得贴了。
值得注意的是,在lg2210的洛谷题解区,有些代码并没有正确地实现模拟退火(当然也能AC)。因此我给出一份我认为正确的伪代码:
- 假设一次循环里面,当前状态和下一状态共用空间。
- 以下伪代码的val和状态a总是同步的。
- 下文给出的模拟退火代码都是基于这个伪代码。
- 如果需要记录最优解,只需要再开一个变量res,并把ans = min(ans,val);这句展开一下。详见“TSP”那份模拟退火的代码,sa.py。
int sa(double T,double alpha){
生成初始状态a;
int val,ans;val = ans = calc_cost(初始状态a);
while(T > 1e-16){
生成新状态na;
int nval = calc_cost(新状态na);
if(nval < val || 1.0*rand()/RAND_MAX <= exp((val-nval) / T)) val = nval;//accept
else 撤销状态修改;//reject
ans = min(ans,val);
T *= alpha;
}
return ans;
}
一个比较有用的技巧:假如一个随机算法(包括但不限于“模拟退火”),有1/c的概率找到最优解。则重复跑c次,得到最优解的概率大大增加。在参数难以做出进一步优化的情况下,这个做法比单纯地把迭代次数乘以c要有效。
模拟退火求解TSP
城市数据如下
cities = [[0.6606,0.9695,0.5906,0.2124,0.0398,
0.1367,0.9536,0.6091,0.8767,0.8148,
0.3876,0.7041,0.0213,0.3429,0.7471,
0.5449,0.9464,0.1247,0.1636,0.8668],
[0.9500,0.6740,0.5029,0.8274,0.9697,
0.5979,0.2184,0.7148,0.2395,0.2867,
0.8200,0.3296,0.1649,0.3025,0.8192,
0.9392,0.8191,0.4351,0.8646,0.6768]]
N = len(cities[0])
- cities[0]是x坐标,cities[1]是y坐标,N是城市个数。
- 为了方便,城市编号为0~N-1。
TSP有状压dp解法。我们给状压dp加一个path数组,记录每个状态的决策点,即可获取TSP问题的一个路径。
dp[i,S]表示现在位于i,已经走过的城市集合为S的最小路径长度。必须保证S的第i位为1。
为了方便,我们约定起点是0号点,则状态S只需枚举奇数。
因为要最后一个被访问的点i回到0号点,所以答案是
min(dp[i][(1<<N)-1] + dis(i,0)),i = 0~N-1
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
#define rep(i,a,b) for(int i = (a);i <= (b);++i)
#define re_(i,a,b) for(int i = (a);i < (b);++i)
#define dwn(i,a,b) for(int i = (a);i >= (b);--i)
const int N = 20;
const double INF = DBL_MAX/2;
double cities[2][N] = {{0.6606,0.9695,0.5906,0.2124,0.0398,
0.1367,0.9536,0.6091,0.8767,0.8148,
0.3876,0.7041,0.0213,0.3429,0.7471,
0.5449,0.9464,0.1247,0.1636,0.8668},
{0.9500,0.6740,0.5029,0.8274,0.9697,
0.5979,0.2184,0.7148,0.2395,0.2867,
0.8200,0.3296,0.1649,0.3025,0.8192,
0.9392,0.8191,0.4351,0.8646,0.6768}};
double dp[N+2][(1<<N)+5];
int path[N+2][(1<<N)+5];
void dbg(){puts("");}
template<typename T, typename... R>void dbg(const T &f, const R &... r) {
cout << f << " ";
dbg(r...);
}
template<typename Type>inline void read(Type &xx){
Type f = 1;char ch;xx = 0;
for(ch = getchar();ch < '0' || ch > '9';ch = getchar()) if(ch == '-') f = -1;
for(;ch >= '0' && ch <= '9';ch = getchar()) xx = xx * 10 + ch - '0';
xx *= f;
}
double dis(int x,int y){
return sqrt((cities[0][x]-cities[0][y])*(cities[0][x]-cities[0][y]) + (cities[1][x]-cities[1][y])*(cities[1][x]-cities[1][y]));
}
double solve(){
re_(i,0,N) re_(S,0,1<<N) dp[i][S] = INF;
memset(path,-1,sizeof path);
dp[0][1] = 0;
for(int S = 1;S < (1<<N);S += 2){
re_(i,1,N){
if(!(S >> i & 1)) continue;
re_(j,0,N){
if((!(S >> j & 1)) || i == j) continue;
dp[i][S] = min(dp[i][S],dp[j][S^(1<<i)] + dis(i,j));
if(dp[i][S] < INF && fabs(dp[i][S] - (dp[j][S^(1<<i)] + dis(i,j))) < 1e-8)
path[i][S] = j;
}
}
}
double ans = INF;
re_(i,0,N) ans = min(ans,dp[i][(1<<N)-1] + dis(i,0));
return ans;
}
double jdg(double ans){
int las = -1;
re_(i,0,N){
if(fabs(dp[i][(1<<N)-1]+dis(i,0)-ans) < 1e-8){
las = i;break;
}
}
vector<int> p;
for(int x = las,S = (1<<N)-1;~x;){
p.push_back(x);
int tx = x;
x = path[x][S];
S ^= (1<<tx);
}
reverse(p.begin(),p.end());
for(auto &x: p) cout << x << ",";puts("");//dbg
double val = 0;
re_(i,0,N) val += dis(p[i],p[(i+1)%N]);
return val;
}
int main(int argc, char** argv) {
double ans = solve();
printf("ans = %.10lf\\n",ans);
//dbg
double val = jdg(ans);
printf("val = %.10lf\\n",val);
return 0;
}
输出
状压dp求出最优解:4.0306561826
输出的路径:0,15,10,3,18,4,5,17,12,13,2,11,9,8,6,19,1,16,14,7,
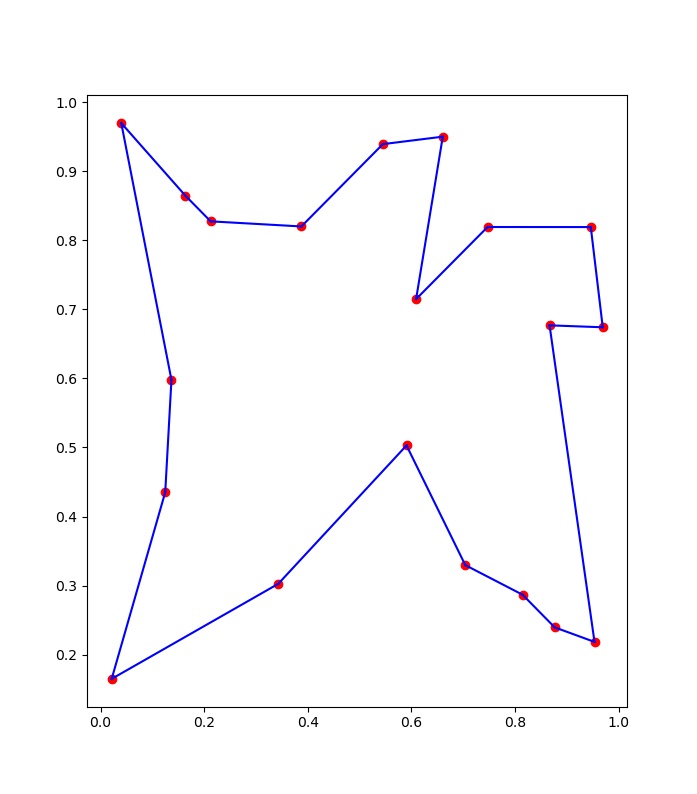
绘图.py,把输出的路径数组复制到下面的p变量,可视化这个最优路径:
- scatter可以画一个点。
- plot可以输入2个点,画一条线。
import math
import os
import copy
import random
import matplotlib.pyplot as plt
import numpy as np
cities = [[0.6606,0.9695,0.5906,0.2124,0.0398,
0.1367,0.9536,0.6091,0.8767,0.8148,
0.3876,0.7041,0.0213,0.3429,0.7471,
0.5449,0.9464,0.1247,0.1636,0.8668],
[0.9500,0.6740,0.5029,0.8274,0.9697,
0.5979,0.2184,0.7148,0.2395,0.2867,
0.8200,0.3296,0.1649,0.3025,0.8192,
0.9392,0.8191,0.4351,0.8646,0.6768]]
N = len(cities[0])
def calc_cost(x,y):
res = 0
for i in range(N):
res += math.sqrt((x[i]-x[(i+1)%N])**2 + (y[i]-y[(i+1)%N])**2)
return res
def draw(x,y):
plt.scatter(x,y,color = "r")
for i in range(N):
plt.plot([x[i],x[(i+1)%N]],[y[i],y[(i+1)%N]],color = "b")
if __name__ == '__main__':
p = [0,15,10,3,18,4,5,17,12,13,2,11,9,8,6,19,1,16,14,7]
x,y = [cities[0][i] for i in p],[cities[1][i] for i in p]
print(calc_cost(x,y))
draw(x,y)
plt.show()
模拟退火有两个参数,T=初始温度,alpha=系数。alpha用于更新T。一般我们都是采用这个式子来更新T:
T *= alpha
接受较差解的概率,也采用标准公式即可:
math.exp(-deltaE / T)
代码里要求提供迭代次数M,这个可以删了,把循环条件改成T > 1e-16之类的。
我们使用上文所说的技巧,运行7次模拟退火取最优。针对上面20个城市的数据,跑出全局最优解的概率,貌似不算很小。
sa.py
import math
import os
import copy
import random
import matplotlib.pyplot as plt
import numpy as np
cities = [[0.6606,0.9695,0.5906,0.2124,0.0398,
0.1367,0.9536,0.6091,0.8767,0.8148,
0.3876,0.7041,0.0213,0.3429,0.7471,
0.5449,0.9464,0.1247,0.1636,0.8668],
[0.9500,0.6740,0.5029,0.8274,0.9697,
0.5979,0.2184,0.7148,0.2395,0.2867,
0.8200,0.3296,0.1649,0.3025,0.8192,
0.9392,0.8191,0.4351,0.8646,0.6768]]
N = len(cities[0])
def calc_cost(a):
res = 0
for i in range(N):
res += math.sqrt((a[0][i]-a[0][(i+1)%N])**2 + (a[1][i]-a[1][(i+1)%N])**2)
return res
def sa(M,T,alpha):
res,a = copy.deepcopy(cities),copy.deepcopy(cities)
ans = calc_cost(res)
val = ans
for _ in range(M):
p1,p2 = random.randint(0,N-1),random.randint(0,N-1)
a[0][p1],a[0][p2],a[1][p1],a[1][p2] = a[0][p2],a[0][p1],a[1][p2],a[1][p1]
nval = calc_cost(a)
deltaE = nval - val
if deltaE < 0 or random.random() <= math.exp(-deltaE / T):
val = nval
else:
a[0][p1],a[0][p2],a[1][p1],a[1][p2] = a[0][p2],a[0][p1],a[