预测模型基于樽海鞘算法的极限学习机（ELM）回归预测 Matlab代码

Posted 2021-08-02 MatlabQQ1575304183

一、极限学习机

       单隐藏层反馈神经网络具有两个比较突出的能力： 

（1）可以直接从训练样本中拟 合 出 复 杂 的 映 射 函 数f :x ^ t 

（2 ）可以为大量难以用传统分类参数技术处理的自然或者人工现象提供模型。但是单隐藏层反馈神经网络缺少比较快速的学习方 法 。误差反向传播算法每次迭代需要更新n x(L+ 1) +L x (m+ 1 )个 值 ，所花费的时间远远低于所容忍的时间。经常可以看到为训练一个单隐藏层反馈神经网络花费了数小时，数天或者更多的时间。
       基于以上原因，黄广斌教授对单隐藏层反馈神经网络进行了深入的研究，提
出并证明了两个大胆的理论：

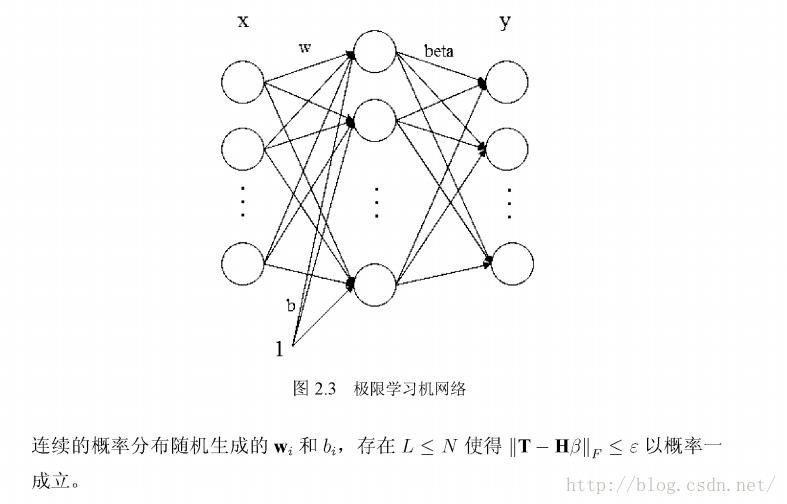
       从以上两条理论我们可以看出，只要激励函数g:R ^ R满足在任意区间上无限可微，那么wt和bt可以从R的n维和R空间的任何区间内根据任意连续的概率分布随机生成 ，也就是说单隐藏层前馈神经网络无需再对wt和bt进行调整；又因为式子||TH*beta||_f=0以概率一成立，我们发现输出层的偏置也不再需要。那么一个新型的但隐藏层反馈神经网络如图2 .3表示 。
对比图2.2,缺少了输出层偏 置bs,而输入权重w和隐藏层偏置bi随机产生不需要调整，那么整个网络仅仅剩下输出权重beta一项没有确定。因此极限学习机
应运而生。令神经网络的输出等于样本标签，如式 (2-11) 表示

n x(L+1) +Lx(m+1)个值,且反向传播算法为了保证系统的稳定性通常选取较小的学习率，使得学习时间大大加长。因此极限学习机在这一方法优势非常巨大，在实验中 ，极限学习机往往在数秒内就完成了运算。而一些比较经典的算法在训练一个单隐藏层神经网络的时候即使是很小的应用也要花费大量的时间，似乎这些算法存在着一个无法逾越的虚拟速度壁垒。

(2)在大多数的应用中，极限学习机的泛化能力大于类似于误差反向传播算法这类的基于梯度的算法。
( 3 ) 传统的基于梯度的算法需要面对诸如局部最小，合适的学习率、过拟合等问题 ，而极限学习机一步到位直接构建起单隐藏层反馈神经网络，避免了这些难以处理的棘手问题。
极限学习机由于这些优势，广大研究人员对极限学习机报以极大的兴趣，使得这几年极限学习机的理论发展很快，应用也在不断地拓宽。

二、樽海鞘算法

樽海鞘是一种透明的桶状生物，和水母比较相似。它通过吸水、喷水来移动的。由于它生活在寒带的深海里面，给我们的研究造成了一定的困扰。但是，这并不影响我们对它的研究。在深海里，樽海鞘是以樽海鞘链的形式存在，这就是我们感兴趣的群体行为之一。

　　首先，我们将樽海鞘链分为两组：1、领导者；2、追随者。

　　领导者就是樽海鞘链前端的部分；追随者就是樽海鞘链后端的部分。

　　首先，领导者的位置跟新公式：

　　

更新追随者位置

　　

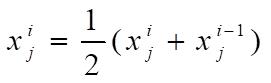
三、代码

% 为适应网络结构 做转置
%%  数据归一化
p_train=p_train';%n*m数据，n是输入特征数量，m是样本数量
t_train=t_train';%n*m数据，n是输入特征数量，m是样本数量
% [p_train, ps_input] = mapminmax(p_train,0,1);
% [t_train, ps_output] = mapminmax(t_train,0,1);
p_test=p_test';
% [p_test ] = mapminmax(p_test' ,0,1);
% p_test = mapminmax('apply',p_test',ps_input);

%% 网络的建立和训练
% 利用循环，设置不同的隐藏层神经元个数
nn=[7 11 14 18];
shuchu=1;%输出结果维度
for i=1:4
    threshold=[0 2;0 2];%几个n几个[0,1]
    % 建立Elman神经网络 隐藏层为nn(i)个神经元
    net=newelm(threshold,[nn(i),shuchu],{'tansig','purelin'});%几个输出几个
    % 设置网络训练参数
    net.trainparam.epochs=2000;
    net.trainparam.show=20;
    net.trainParam.showWindow = false;
net.trainParam.showCommandLine = false; 
    % 初始化网络
    net=init(net);
    % Elman网络训练
    net=train(net,p_train,t_train);
    % 预测数据
    y=sim(net,p_test)*1000/25;%% 数据反归一化
%     y= mapminmax('reverse',y,ps_output);
    % 计算误差
%     error(i,:)=y'-t_test;
        rmse(i)=sqrt(mse(y'-t_test));
        error(i,:)=y';
end

预测结果如下图

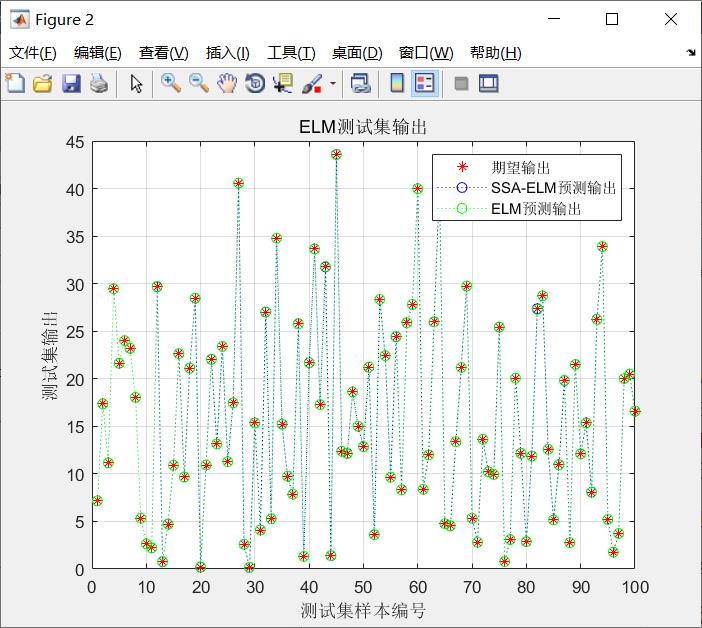
误差曲线：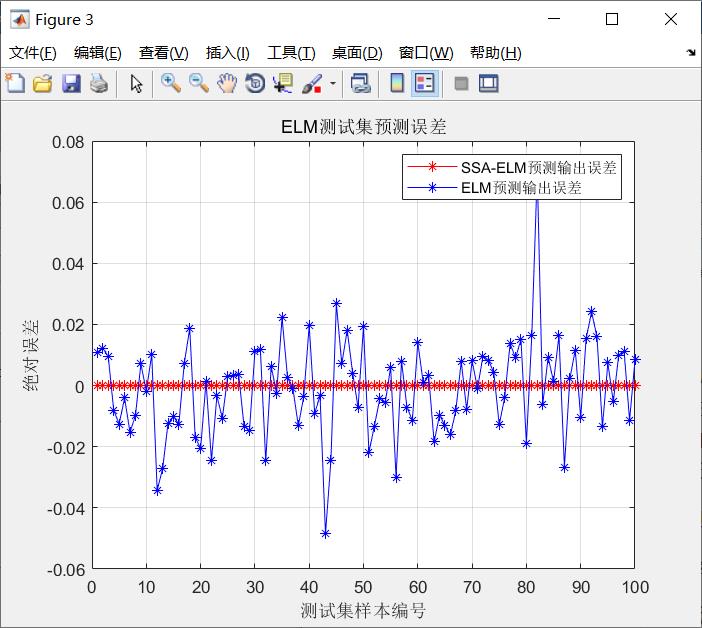

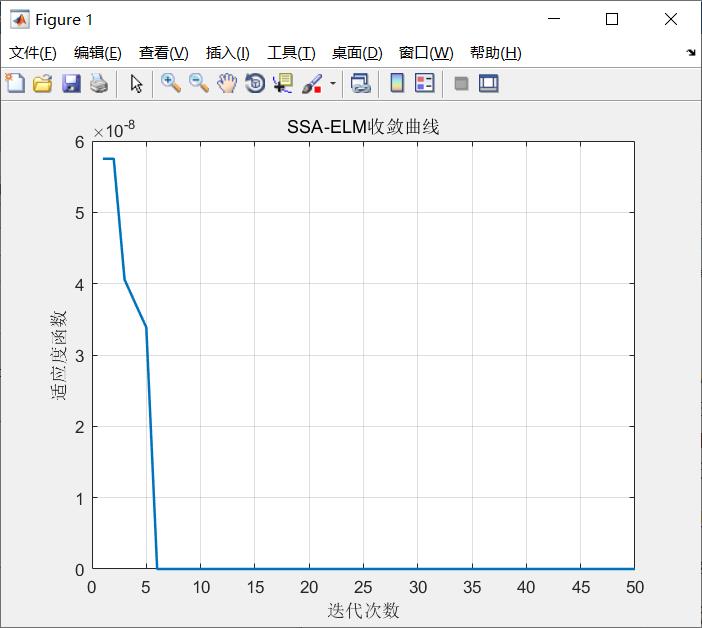
四、参考文献