数学建模基于matlab UKF自行车状态估计含Matlab源码 1111期

Posted 2021-08-02 紫极神光（Q1564658423）

一、简介

著名学者Julier等提出近似非线性函数的均值和方差远比近似非线性函数本身更容易，因此提出了基于确定性采样的UKF算法。
该算法的核心思想是：采用UT变换，利用一组Sigma采样点来描述随机变量的高斯分布，然后通过非线性函数的传递，再利用加权统计线性回归技术来近似非x线性函数的后验均值和方差。
相比于EKF，UKF的估计精度能够达到泰勒级数展开的二阶精度。

1 UT变换

2 采样策略
根据Sigma点采样策略不同，相应的Sigma点以及均值权值和方差权值也不尽相同，因此UT变换的估计精度也会有差异，但总体来说，其估计精度能够达到泰勒级数展开的二阶精度。
为保证随机变量x经过采样之后得到的Sigma采样点仍具有原变量的必要特性，所以采样点的选取应满足：

下面介绍两种经常使用的采样策略：比例采样和比例修正对称采样

3 UKF算法流程

二、源代码

%% UKF bicycle test
clear all
close all

% load params from file
load('bicycle_data.mat') 

use_laser = 1;
use_radar = 1;

stop_for_sigmavis = false;

%% Data Initialization
x_pred_all = []; % predicted state history
x_est_all = []; % estimated state history with time at row number 6
NIS_radar_all = []; % estimated state history with time at row number 6
NIS_laser_all = []; % estimated state history with time at row number 6

est_pos_error_squared_all = [];
laser_pos_error_squared_all = [];

P_est = 0.2*eye(n_x); % initial uncertainty matrix
P_est(4,4) = 0.3; % initial uncertainty
P_est(5,5) = 0.3; % initial uncertainty

%% process noise

acc_per_sec = 0.3; % acc in m/s^2 per sec
yaw_acc_per_sec = 0.3; % yaw acc in rad/s^2 per sec


Z_l_read = [];

std_las1 = 0.15;
std_las2 = 0.15;

std_radr = 0.3;
std_radphi = 0.03;
std_radrd = 0.3;


% UKF params
n_aug = 7;
kappa = 3-n_aug;

w = zeros(2*n_aug+1,1);
w(1) = kappa/(kappa+n_aug);

for i=2:(2*n_aug+1)
  w(i) = 0.5/(n_aug+kappa);
end

%% UKF filter recursion
%x_est_all(:,1) = GT(:,1);
Xi_pred_all = [];
Xi_aug_all = [];
x_est = [0.1 0.1 0.1 0.1 0.01];
last_time = 0;


% load measurement data from file
fid = fopen('obj_pose-laser-radar-synthetic-ukf-input.txt');

%% State Initialization
tline = fgets(fid); % read first line

% find first laser measurement
while tline(1) ~= 'L' % laser measurement
    tline = fgets(fid); % go to next line
end
    
line_vector = textscan(tline,'%s %f %f %f %f %f %f %f %f %f');
last_time = line_vector{4};% get timestamp
x_est(1) = line_vector{2}; % initialize position p_x
x_est(2) = line_vector{3}; % initialize position p_y

tline = fgets(fid); % go to next line 

% counter 
k = 1;
while ischar(tline)  % go through lines of data file
    
    % find time of measurement
    if tline(1) == 'L' % laser measurement
        if use_laser == false
            tline = fgets(fid); % skip this line and go to next line
            continue;
        else % read laser meas time
            line_vector = textscan(tline,'%s %f %f %f %f %f %f %f %f %f');
            meas_time = line_vector{1,4};
        end
    elseif  tline(1) == 'R' % radar measurement 
        if use_radar == false
            tline = fgets(fid); % skip this line and go to next line
            continue;
        else % read radar meas time
            line_vector = textscan(tline,'%s %f %f %f %f %f %f %f %f %f %f');
            meas_time = line_vector{5};
        end
    else % neither laser nor radar
        disp('Error: not laser nor radar')
        return;
    end
    
    
    delta_t_sec = ( meas_time - last_time ) / 1e6; % us to sec
    last_time = meas_time;

    
    %% Prediction part
    p1 = x_est(1);
    p2 = x_est(2);
    v = x_est(3);
    yaw = x_est(4);
    yaw_dot = x_est(5); % yaw_dot: yaw velocity
    x = [p1; p2; v; yaw; yaw_dot]; % state vector
    
    
    std_a = acc_per_sec;         % process noise long. acceleration
    std_ydd = yaw_acc_per_sec;   % process noise yaw acceleration
  
    if std_a == 0
        std_a = 0.0001;
    end
    if std_ydd == 0
        std_ydd = 0.0001;
    end
    % Create sigma points
    x_aug = [x ; 0 ; 0];
    P_aug = [P_est zeros(n_x,2) ; zeros(2,n_x) [std_a^2 0 ; 0 std_ydd^2 ]];
    
    %P_aug = nearestSPD(P_aug);
    
    Xi_aug = zeros(n_aug,2*n_aug+1);
    sP_aug = chol(P_aug,'lower'); % Cholesky factorization.
    Xi_aug(:,1) = x_aug;
    
    for i=1:n_aug
        Xi_aug(:,i+1) = x_aug + sqrt(n_aug+kappa) * sP_aug(:,i);
        Xi_aug(:,i+1+n_aug) = x_aug - sqrt(n_aug+kappa) * sP_aug(:,i);
    end
    
    
    % Predict sigma points
    Xi_pred = zeros(n_x,2*n_aug+1);
    for i=1:(2*n_aug+1)
        p1 = Xi_aug(1,i);
        p2 = Xi_aug(2,i);
        v = Xi_aug(3,i);
        yaw = Xi_aug(4,i);
        yaw_dot = Xi_aug(5,i);
        
        nu_a = Xi_aug(6,i);
        nu_yaw_dd = Xi_aug(7,i);
        
        if abs(yaw_dot) > 0.001 %turn around
            p1_p = p1 + v/yaw_dot * ( sin (yaw + yaw_dot*delta_t_sec) - sin(yaw));
            p2_p = p2 + v/yaw_dot * ( cos(yaw) - cos(yaw+yaw_dot*delta_t_sec) );
        else                    %not turn around
            p1_p = p1 + v*delta_t_sec*cos(yaw);
            p2_p = p2 + v*delta_t_sec*sin(yaw);
        end
        
        v_p = v;
        yaw_p = yaw + yaw_dot*delta_t_sec;
        yaw_dot_p = yaw_dot;
        
        % add noise
        p1_p = p1_p + 0.5*nu_a*delta_t_sec^2 * cos(yaw);
        p2_p = p2_p + 0.5*nu_a*delta_t_sec^2 * sin(yaw);
        v_p = v_p + nu_a*delta_t_sec;
        
        yaw_p = yaw_p + 0.5*nu_yaw_dd*delta_t_sec^2;
        yaw_dot_p = yaw_dot_p + nu_yaw_dd*delta_t_sec;
        
        Xi_pred(1,i) = p1_p;
        Xi_pred(2,i) = p2_p;
        Xi_pred(3,i) = v_p;
        Xi_pred(4,i) = yaw_p;
        Xi_pred(5,i) = yaw_dot_p;
    end
    
    % average and covar of sigma points
    x_pred = 0;
    P_pred = zeros(5,5);
    
    for i=1:2*n_aug+1
        x_pred = x_pred + w(i)* Xi_pred(:,i);
    end
    
    
    for i=1:2*n_aug+1
        P_pred = P_pred + w(i)* (Xi_pred(:,i) - x_pred)*(Xi_pred(:,i) - x_pred)';
    end
    
    

    %% visualize sigma point examples
    if stop_for_sigmavis && k == 25
        disp('Stopping for sigma point visualization');
        
        % 2d example
        P_s = P_est (1:2,1:2);
        x_s = x(1:2);
        Xi_s = zeros(2,5);
        A = chol(P_s,'lower');
        Xi_s(:,1) = x_s;
        
        for i=1:2
            Xi_s(:,i+1) = x_s + sqrt(3) * A(:,i);
            Xi_s(:,i+1+2) = x_s - sqrt(3) * A(:,i);
        end
        
        error_ellipse(P_s,x_s,'conf', 0.4, 'style', 'k-');
        
        Xi_aug_p1 =  squeeze(Xi_s(1,:,:));
        Xi_aug_p2 =  squeeze(Xi_s(2,:,:));
        
        hold on;
        plot(Xi_aug_p1, Xi_aug_p2, 'or');
        legend('P', 'sigma points')
        axis equal
        
        xlabel('p_x in m');
        ylabel('p_y in m');
        
        save('sigma_visualization.mat', 'x_s','P_s','A','Xi_s', 'Xi_aug', 'Xi_pred');
        
        %return;
    end
    k=k+1;

三、运行结果

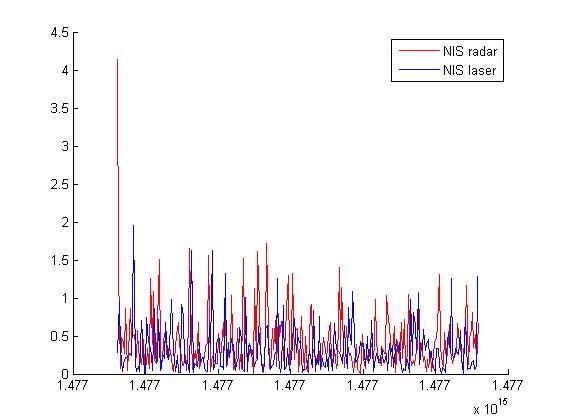
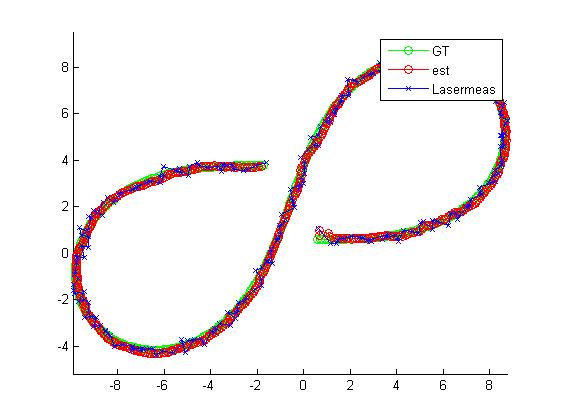
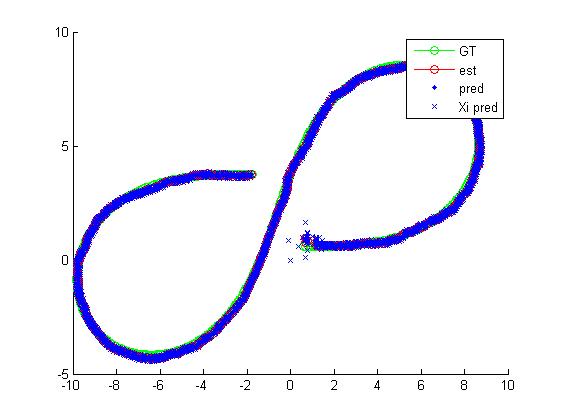
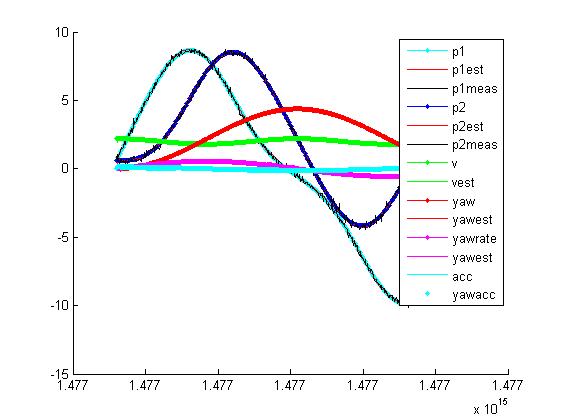
四、备注

版本：2014a