P1908 逆序对

Posted 2021-08-01 诸葛阵御

题目描述

猫猫 TOM 和小老鼠 JERRY 最近又较量上了，但是毕竟都是成年人，他们已经不喜欢再玩那种你追我赶的游戏，现在他们喜欢玩统计。

最近，TOM 老猫查阅到一个人类称之为“逆序对”的东西，这东西是这样定义的：对于给定的一段正整数序列，逆序对就是序列中 a_i>a_j​ 且 i<j 的有序对。知道这概念后，他们就比赛谁先算出给定的一段正整数序列中逆序对的数目。注意序列中可能有重复数字。

Update:数据已加强。

输入格式

第一行，一个数 n，表示序列中有 n个数。

第二行 n 个数，表示给定的序列。序列中每个数字不超过 10^9。

输出格式

输出序列中逆序对的数目。

输入输出样例

输入 #1复制

6
5 4 2 6 3 1

输出 #1复制

11

说明/提示

对于 25% 的数据，n≤2500

对于 50% 的数据，n≤4×104。

对于所有数据，n≤5×105

请使用较快的输入输出

应该不会 O(n2) 过 50 万吧 by chen_zhe

思路

请放弃双for循环，数据中 10^9 代表着会超时

推荐使用归并排序

-归并排序

简述：

归并的主要思想是分治

分治：将大问题分成多个小问题解决，最后将小问题合并，则可以解决大问题

将数组逐层拆分，排序后合并，合并后的数组即为排序后的数组

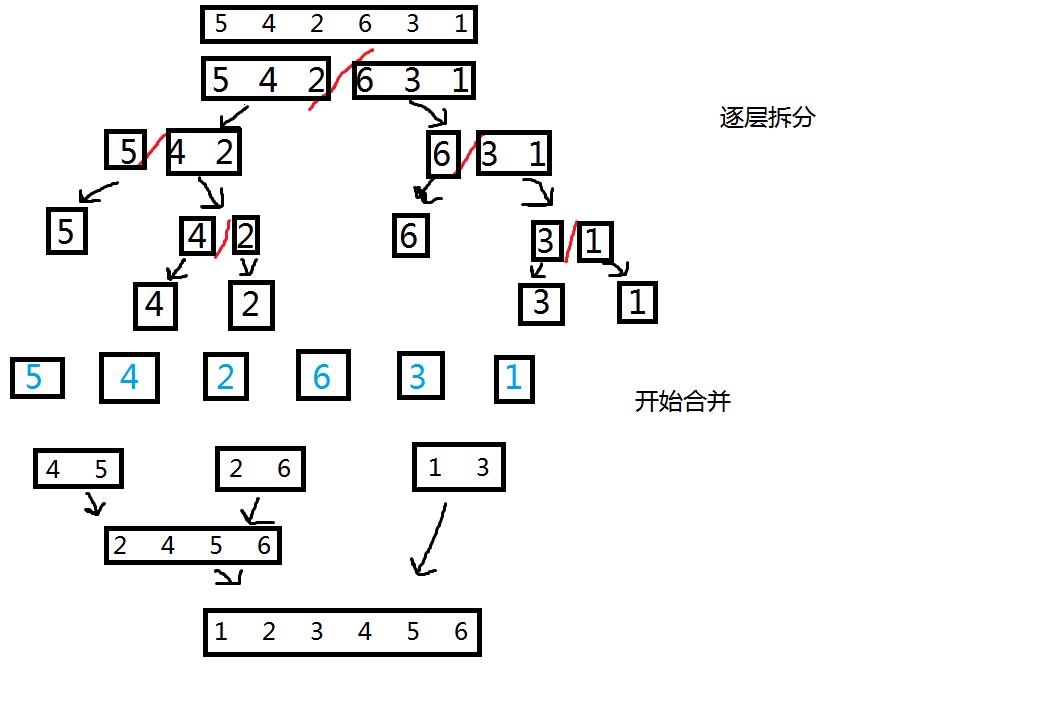
合并时如何排序？

合并时比较两个子数组的头元素，将较小的元素存入临时数组，下标++（即指向较小元素所在数组的下标）

代码

#include <stdio.h>
#include <iostream>
using namespace std;
long long int ans=0;
long long int a[500005];	//原数组 
long long int b[500005];	//临时数组（排序用） 
	//归并排序 
void msort(int l,int r) {	// l 为左下标， r 为右下标 
	if (l==r) {	//左下标与右下标重合代表只有一个数据，不执行操作 
		return; 
	}
	int mid=(l+r)/2;	//数组中间点 
	msort(l,mid);	//递归二分左边数组 
	msort(mid+1,r);	//递归二分右边数组 

	int i=l;	//左子数组（l ~ mid)用下标 
	int j=mid+1;	//右子数组(mid+1 ~ r用下标 
	int t=l;	//临时数组用下标 
	
	while (i<=mid&&j<=r) {
		if (a[i]>a[j]) { 
			ans=ans+(mid-i+1);	//因为子数组有序，若a(i)>a(j),则i~mid的元素均>a(j) 
			b[t]=a[j];	//将最小的a(j)放入b数组 
			t++;
			j++;
		} else {
			b[t]=a[i];
			t++;
			i++;
		}
	}
	while (i<=mid) {	//将剩余的数存进b数组 
		b[t]=a[i];
		t++;
		i++;
	}
	while (j<=r) {	//同上 
		b[t]=a[j];
		t++;
		j++;
	}
	for (int i=l;i<=r;i++) {	//将临时数组复制到原数组 
		a[i]=b[i];
	}
}
int main()
{
	long long int n;
	cin>>n;
	for (long long int i=1;i<=n;i++) {	//输入 
		cin>>a[i];
	}
	msort(1,n);	//调用函数
	cout<<ans;	//输出 
	return 0;
}