树的定义基本术语以及常考性质（C语言）

Posted 2021-08-01 bfhonor

一、树的定义和基本术语

（一）基本概念

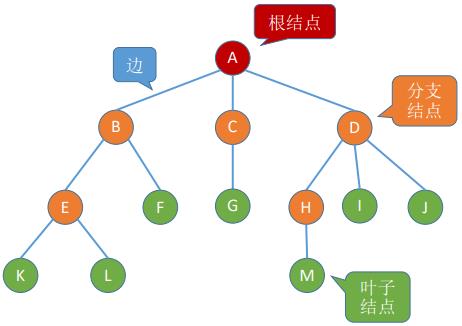
• ∅ 空树——结点数为0的树
• 非空树的特性：
  🌲有且仅有一个根节点
  🌲没有后继的结点称为“叶子结点”（或终端结点）
  🌲有后继的结点称为“分支结点”（或非终端结点）
  🌲除了根节点外，任何一个结点都有且仅有一个前驱
  🌲每个结点可以有0个或多个后继。
  
• 除了根节点外，任何一个结点都有且仅有一个前驱
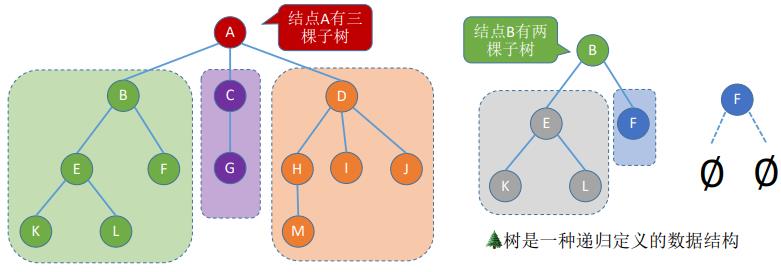
• 树是n（n≥0）个结点的有限集合，n = 0时，称为空树，这是一种特殊情况。在任意一棵非空树中应满足：
  ①、有且仅有一个特定的称为根的结点。
  ②、当n > 1时，其余结点可分为m（m > 0）个互不相交的有限集合T1，T2，…，T_m，其中每个集合本身又是一棵树，并且称为根结点的 子树 。
  

（二）基本术语

1. 结点之间的关系描述

• 祖先结点：对于任何节点n ，它的祖先是位于根到节点n之间的路径上的节点。
• 子孙结点：一个结点含有的子树的根结点的子节点。
• 双亲结点（父节点）：若一个结点含有子结点，则这个结点称为其子结点的父结点。
• 孩子结点：一个结点含有的子树的根结点称为该结点的子结点。
• 兄弟结点：具有相同父结点的结点互称为兄弟结点
• 堂兄弟结点：如果树的两个节点深度相同，但父节点不同，则它们是一对堂兄弟节点。
• 什么是两个结点之间的路径？【只能从上往下】
• 什么是路径长度？【经过几条边】

2. 结点、树的属性描述

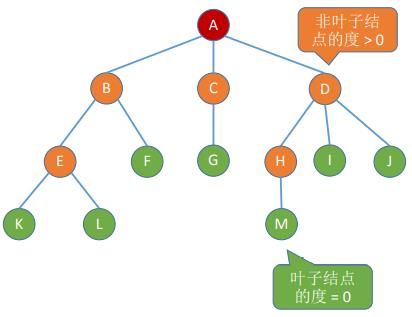
• 属性：
  ①、结点的层次（深度）——从上往下数 【默认从1开始】
  ②、结点的高度——从下往上数
  ③、树的高度（深度）——总共多少层
  ④、结点的度——有几个孩子（分支）
  ⑤、树的度——各结点的度的最大值

3. 有序树、无序树

• 有序树——逻辑上看，树中结点的各子树从左至右是有次序的，不能互换
• 无序树——逻辑上看，树中结点的各子树从左至右是无次序的，可以互换

4. 森林

• 森林。森林是m（m≥0）棵互不相交的树的集合
• m可为0，空森林
  

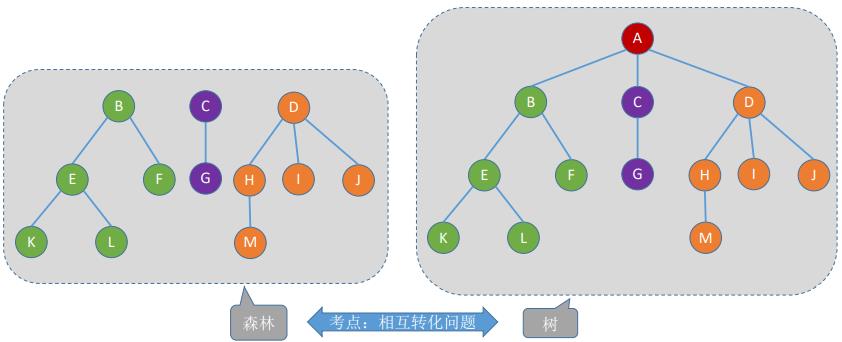
二、树—常考性质

（一）常见考点1：结点数=总度数+1

• 结点的度——结点有几个孩子（分支）

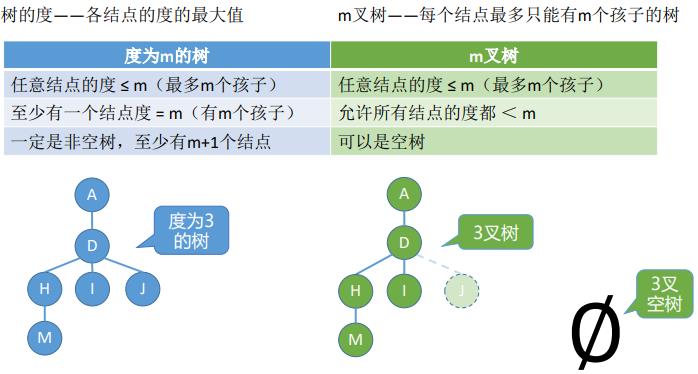
（二）常见考点2：度为m的树、m叉树的区别

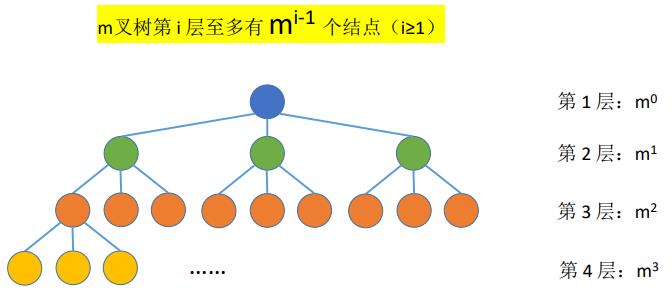
（三）常见考点3：度为m的树第 i 层至多有 m^i-1个结点（i≥1）

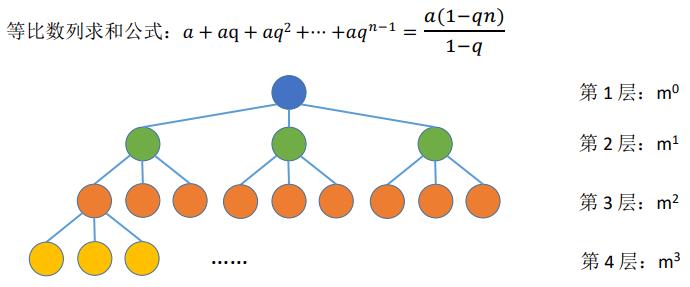
（四）常见考点4：高度为h的m叉树至多有(m^h-1)/(m-1)个结点。

（五）常见考点5：高度为h的m叉树至少有 h 个结点。

（六）常见考点6：具有n个结点的m叉树的最小高度为 「logm(n(m - 1) + 1)」