隔壁老王都会了，你竟然还不知道？Redis zset底层—Skip List跳跃列表（面试超级加分项）

Posted 2021-08-01 李子捌

一、简介

跳表全称叫做跳跃表，简称跳表。跳表是一个随机化的数据结构，实质就是一种可以进行二分查找的有序链表。跳表在原有的有序链表上面增加了多级索引，通过索引来实现快速查找。跳表不仅能提高搜索性能，同时也可以提高插入和删除操作的性能。

Skip List(跳跃列表)这种随机的数据结构，可以看做是一个二叉树的变种，它在性能上与红黑树、AVL树很相近；但是Skip List(跳跃列表)的实现相比前两者要简单很多，目前Redis的zset实现采用了Skip List(跳跃列表)（其它还有LevelDB等也使用了跳跃列表）。
​

RBT红黑树与Skip List(跳跃列表)简单对比：
RBT红黑树

1. 插入、查询时间复杂度O(logn)
2. 数据天然有序
3. 实现复杂，设计变色、左旋右旋平衡等操作
4. 需要加锁

Skip List跳跃列表

1. 插入、查询时间复杂度O(logn)
2. 数据天然有序
3. 实现简单，链表结构
4. 无需加锁

二、Skip List算法分析

2.1 Skip List论文

这里贴出Skip List的论文，需要详细研究的请看论文，下文部分公式、代码、图片出自该论文。
Skip Lists: A Probabilistic Alternative to Balanced Trees

https://www.cl.cam.ac.uk/teaching/2005/Algorithms/skiplists.pdf

2.2 Skip List动态图

先通过一张动图来了解Skip List的插入节点元素的流程，此图来自维基百科。

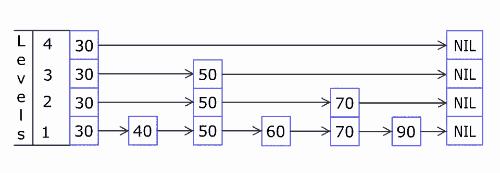
a50f862e502f718e490117c7a6541784.gif

2.3 Skip List算法性能分析

2.3.1 计算随机层数算法

首先分析的是执行插入操作时计算随机数的过程，这个过程会涉及层数的计算，所以十分重要。对于节点他有如下特性：

• 节点都有第一层的指针
• 节点有第i层指针，那么第i+1层出现的概率为p
• 节点有最大层数限制，MaxLevel

计算随机层数的伪代码：

论文中的示例

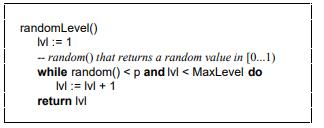
Java版本

1public int randomLevel(){
2    int level = 1;
3    // random()返回一个[0...1)的随机数
4    while (random() < p && level < MaxLevel){ 
5        level += 1;
6    }
7    return level;
8}

代码中包含两个变量P和MaxLevel，在Redis中这两个参数的值分别是：

1p = 1/4
2MaxLevel = 64

2.3.2 节点包含的平均指针数目

Skip List属于空间换时间的数据结构，这里的空间指的就是每个节点包含的指针数目，这一部分是额外的内内存开销，可以用来度量空间复杂度。random()是个随机数，因此产生越高的节点层数，概率越低（Redis标准源码中的晋升率数据1/4，相对来说Skip List的结构是比较扁平的，层高相对较低）。其定量分析如下：

• level = 1 概率为1-p
• level >=2 概率为p
• level = 2 概率为p(1-p)
• level >= 3 概率为p^2
• level = 3 概率为p^2(1-p)
• level >=4 概率为p^3
• level = 4 概率为p^3(1-p)
• ……

得出节点的平均层数（节点包含的平均指针数目）：

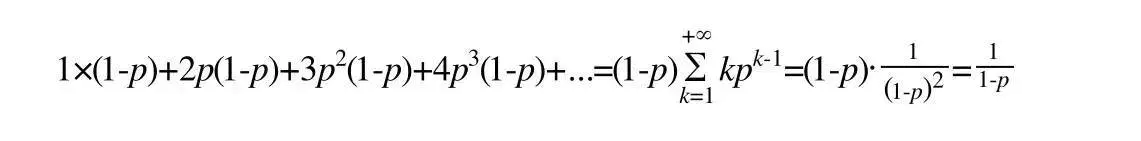
所以Redis中p=1/4计算的平均指针数目为1.33
 

2.3.3 时间复杂度计算

以下推算来自论文内容
假设p=1/2，在以p=1/2生成的16个元素的跳过列表中，我们可能碰巧具有9个元素，1级3个元素，3个元素3级元素和1个元素14级（这不太可能，但可能会发生）。我们该怎么处理这种情况？如果我们使用标准算法并在第14级开始我们的搜索，我们将会做很多无用的工作。那么我们应该从哪里开始搜索？此时我们假设SkipList中有n个元素，第L层级元素个数的期望是1/p个；每个元素出现在L层的概率是p^(L-1), 那么第L层级元素个数的期望是 n * (p^L-1)；得到1 / p =n * (p^L-1)

11 / p = n * (p^L-1)
2n = (1/p)^L
3L = log(1/p)^n

所以我们应该选择MaxLevel = log(1/p)^n
定义：MaxLevel = L(n) = log(1/p)^n
​

推算Skip List的时间复杂度，可以用逆向思维，从层数为i的节点x出发，返回起点的方式来回溯时间复杂度，节点x点存在两种情况：

• 节点x存在(i+1)层指针，那么向上爬一级，概率为p，对应下图situation c.
• 节点x不存在(i+1)层指针，那么向左爬一级，概率为1-p，对应下图situation b.

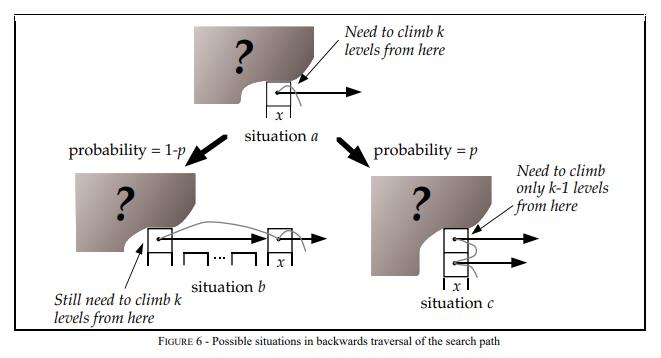
设C(k) = 在无限列表中向上攀升k个level的搜索路径的预期成本（即长度）那么推演如下：

1C(0)=0
2C(k)=(1-p)×(情况b的查找长度) + p×(情况c的查找长度)
3C(k)=(1-p)(C(k)+1) + p(C(k-1)+1)
4C(k)=1/p+C(k-1)
5C(k)=k/p

上面推演的结果可知，爬升k个level的预期长度为k/p，爬升一个level的长度为1/p。

由于MaxLevel = L(n)， C(k) = k / p，因此期望值为：(L(n) – 1) / p；将L(n) = log(1/p)^n 代入可得：(log(1/p)^n - 1) / p；将p = 1 / 2 代入可得：2 * log2^n - 2，即O(logn)的时间复杂度。

三、Skip List特性及其实现

3.1 Skip List特性

Skip List跳跃列表通常具有如下这些特性

1. Skip List包含多个层，每层称为一个level，level从0开始递增
2. Skip List 0层，也就是最底层，应该包含所有的元素
3. 每一个level/层都是一个有序的列表
4. level小的层包含level大的层的元素，也就是说元素A在X层出现，那么 想X>Z>=0的level/层都应该包含元素A
5. 每个节点元素由节点key、节点value和指向当前节点所在level的指针数组组成

3.2 Skip List查询

假设初始Skip List跳跃列表中已经存在这些元素，他们分布的结构如下所示：

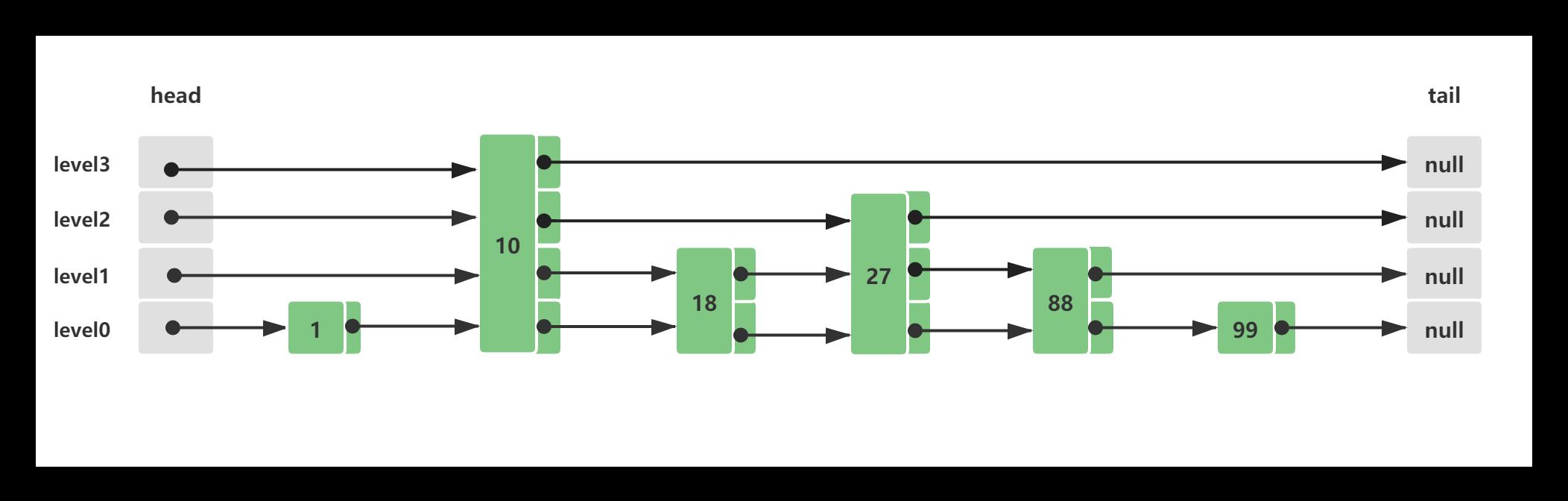
此时查询节点88，它的查询路线如下所示：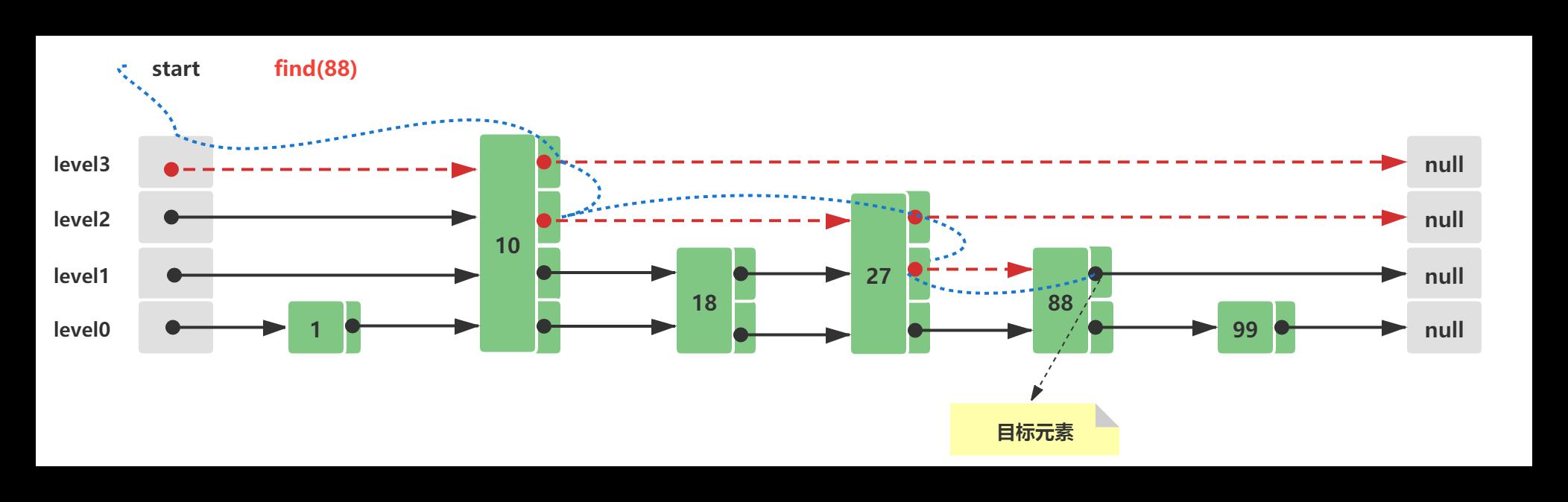

1. 从Skip List跳跃列表最顶层level3开始，往后查询到10 < 88 && 后续节点值为null && 存在下层level2
2. level2 10往后遍历，27 < 88 && 后续节点值为null && 存在下层level1
3. level1 27往后遍历，88 = 88，查询命中

3.3 Skip List插入

Skip List的初始结构与2.3中的初始结构一致，此时假设插入的新节点元素值为90，插入路线如下所示：

1. 查询插入位置，与Skip List查询方式一致，这里需要查询的是第一个比90大的节点位置，插入在这个节点的前面， 88 < 90 < 100
2. 构造一个新的节点Node(90)，为插入的节点Node(90)计算一个随机level，这里假设计算的是1，这个level时随机计算的，可能时1、2、3、4…均有可能，level越大的可能越小，主要看随机因子x ，层数的概率大致计算为 (1/x)^level ，如果level大于当前的最大level3，需要新增head和tail节点
3. 节点构造完毕后，需要将其插入列表中，插入十分简单步骤 -> Node(88).next = Node(90); Node(90).prev = Node(80); Node(90).next = Node(100); Node(100).prev = Node(90);

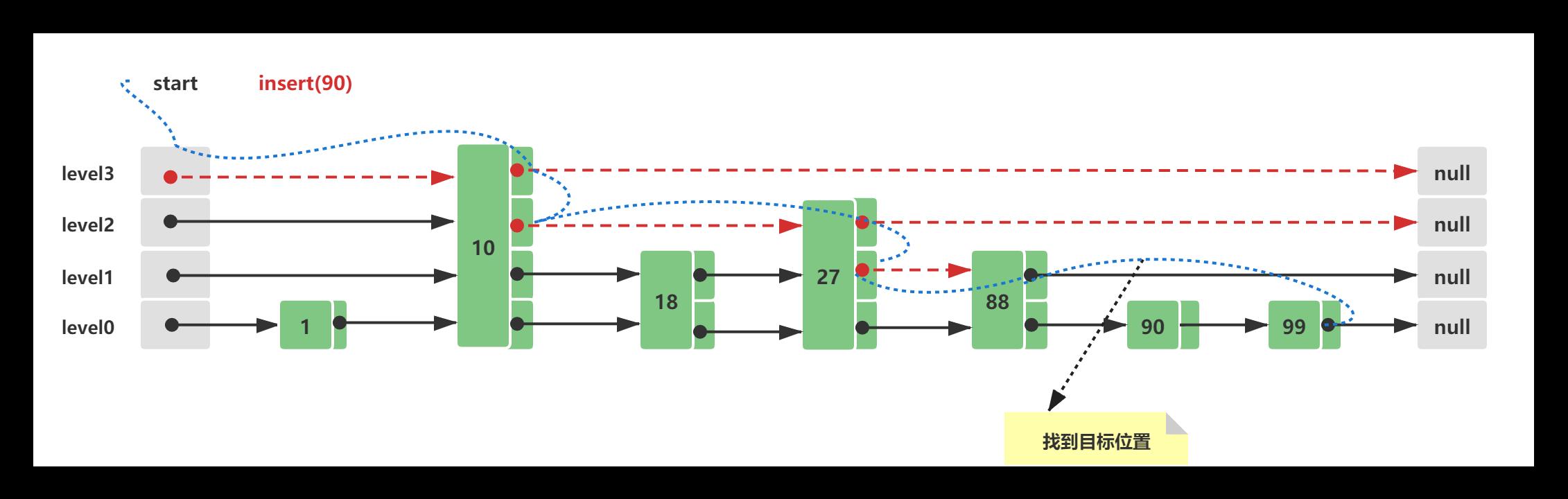
3.4 Skip List删除

删除的流程就是查询到节点，然后删除，重新将删除节点左右两边的节点以链表的形式组合起来即可，这里不再画图
​

四、手写实现一个简单Skip List

实现一个Skip List比较简单，主要分为两个步骤：

1. 定义Skip List的节点Node，节点之间以链表的形式存储，因此节点持有相邻节点的指针，其中prev与next是同一level的前后节点的指针，down与up是同一节点的多个level的上下节点的指针
2. 定义Skip List的实现类，包含节点的插入、删除、查询，其中查询操作分为升序查询和降序查询（往后和往前查询），这里实现的Skip List默认节点之间的元素是升序链表
    

3.1 定义Node节点

Node节点类主要包括如下重要属性：

1. score -> 节点的权重，这个与Redis中的score相同，用来节点元素的排序作用
2. value -> 节点存储的真实数据，只能存储String类型的数据
3. prev -> 当前节点的前驱节点，同一level
4. next -> 当前节点的后继节点，同一level
5. down -> 当前节点的下层节点，同一节点的不同level
6. up -> 当前节点的上层节点，同一节点的不同level

 1package com.liziba.skiplist;
 2
 3/**
 4 * <p>
 5 *      跳表节点元素
 6 * </p>
 7 *
 8 * @Author: Liziba
 9 * @Date: 2021/7/5 21:01
10 */
11public class Node {
12
13    /** 节点的分数值，根据分数值来排序 */
14    public Double score;
15    /** 节点存储的真实数据 */
16    public String value;
17    /** 当前节点的 前、后、下、上节点的引用 */
18    public Node prev, next, down, up;
19
20    public Node(Double score) {
21        this.score = score;
22        prev = next = down = up = null;
23    }
24
25    public Node(Double score, String value) {
26        this.score = score;
27        this.value = value;
28    }
29}

3.2 SkipList节点元素的操作类

SkipList主要包括如下重要属性：

1. head -> SkipList中的头节点的最上层头节点（level最大的层的头节点），这个节点不存储元素，是为了构建列表和查询时做查询起始位置的，具体的结构请看2.3中的结构
2. tail -> SkipList中的尾节点的最上层尾节点（level最大的层的尾节点），这个节点也不存储元素，是查询某一个level的终止标志
3. level -> 总层数
4. size -> Skip List中节点元素的个数
5. random -> 用于随机计算节点level，如果 random.nextDouble() < 1/2则需要增加当前节点的level，如果当前节点增加的level超过了总的level则需要增加head和tail(总level)

  1package com.liziba.skiplist;
  2
  3import java.util.Random;
  4
  5/**
  6 * <p>
  7 *      跳表实现
  8 * </p>
  9 *
 10 * @Author: Liziba
 11 */
 12public class SkipList {
 13
 14    /** 最上层头节点 */
 15    public Node head;
 16    /** 最上层尾节点 */
 17    public Node tail;
 18    /** 总层数 */
 19    public int level;
 20    /** 元素个数 */
 21    public int size;
 22    public Random random;
 23
 24    public SkipList() {
 25        level = size = 0;
 26        head = new Node(null);
 27        tail = new Node(null);
 28        head.next = tail;
 29        tail.prev = head;
 30    }
 31
 32    /**
 33     * 查询插入节点的前驱节点位置
 34     *
 35     * @param score
 36     * @return
 37     */
 38    public Node fidePervNode(Double score) {
 39        Node p = head;
 40        for(;;) {
 41            // 当前层(level)往后遍历，比较score，如果小于当前值，则往后遍历
 42            while (p.next.value == null && p.prev.score <= score)
 43                p = p.next;
 44            // 遍历最右节点的下一层(level)
 45            if (p.down != null)
 46                p = p.down;
 47            else
 48                break;
 49        }
 50        return p;
 51    }
 52
 53    /**
 54     * 插入节点，插入位置为fidePervNode(Double score)前面
 55     *
 56     * @param score
 57     * @param value
 58     */
 59    public void insert(Double score, String value) {
 60
 61        // 当前节点的前置节点
 62        Node preNode = fidePervNode(score);
 63        // 当前新插入的节点
 64        Node curNode = new Node(score, value);
 65        // 分数和值均相等则直接返回
 66        if (curNode.value != null && preNode.value != null && preNode.value.equals(curNode.value)
 67                  && curNode.score.equals(preNode.score)) {
 68            return;
 69        }
 70
 71        preNode.next = curNode;
 72        preNode.next.prev = curNode;
 73        curNode.next = preNode.next;
 74        curNode.prev = preNode;
 75
 76        int curLevel = 0;
 77        while (random.nextDouble() < 1/2) {
 78            // 插入节点层数(level)大于等于层数(level)，则新增一层(level)
 79            if (curLevel >= level) {
 80                Node newHead = new Node(null);
 81                Node newTail = new Node(null);
 82                newHead.next = newTail;
 83                newHead.down = head;
 84                newTail.prev = newHead;
 85                newTail.down = tail;
 86                head.up = newHead;
 87                tail.up = newTail;
 88                // 头尾节点指针修改为新的，确保head、tail指针一直是最上层的头尾节点
 89                head = newHead;
 90                tail = newTail;
 91                ++level;
 92            }
 93
 94            while (preNode.up == null)
 95                preNode = preNode.prev;
 96
 97            preNode = preNode.up;
 98
 99            Node copy = new Node(null);
100            copy.prev = preNode;
101            copy.next = preNode.next;
102            preNode.next.prev = copy;
103            preNode.next = copy;
104            copy.down = curNode;
105            curNode.up = copy;
106            curNode = copy;
107
108            ++curLevel;
109        }
110        ++size;
111    }
112
113    /**
114     * 查询指定score的节点元素
115     * @param score
116     * @return
117     */
118    public Node search(double score) {
119        Node p = head;
120        for (;;) {
121            while (p.next.score != null && p.next.score <= score)
122                p = p.next;
123            if (p.down != null)
124                p = p.down;
125            else // 遍历到最底层
126                if (p.score.equals(score))
127                    return p;
128                return null;
129        }
130    }
131
132    /**
133     * 升序输出Skip List中的元素 （默认升序存储，因此从列表head往tail遍历）
134     */
135    public void dumpAllAsc() {
136        Node p = head;
137        while (p.down != null) {
138            p = p.down;
139        }
140        while (p.next.score != null) {
141            System.out.println(p.next.score + "-->" + p.next.value);
142            p = p.next;
143        }
144    }
145
146    /**
147     * 降序输出Skip List中的元素
148     */
149    public void dumpAllDesc() {
150        Node p = tail;
151        while (p.down != null) {
152            p = p.down;
153        }
154        while (p.prev.score != null) {
155            System.out.println(p.prev.score + "-->" + p.prev.value);
156            p = p.prev;
157        }
158    }
159
160
161    /**
162     * 删除Skip List中的节点元素
163     * @param score
164     */
165    public void delete(Double score) {
166        Node p = search(score);
167        while (p != null) {
168            p.prev.next = p.next;
169            p.next.prev = p.prev;
170            p = p.up;
171        }
172    }
173
174
175}