图论——关键路径

Posted 2021-08-01 牧空

原理

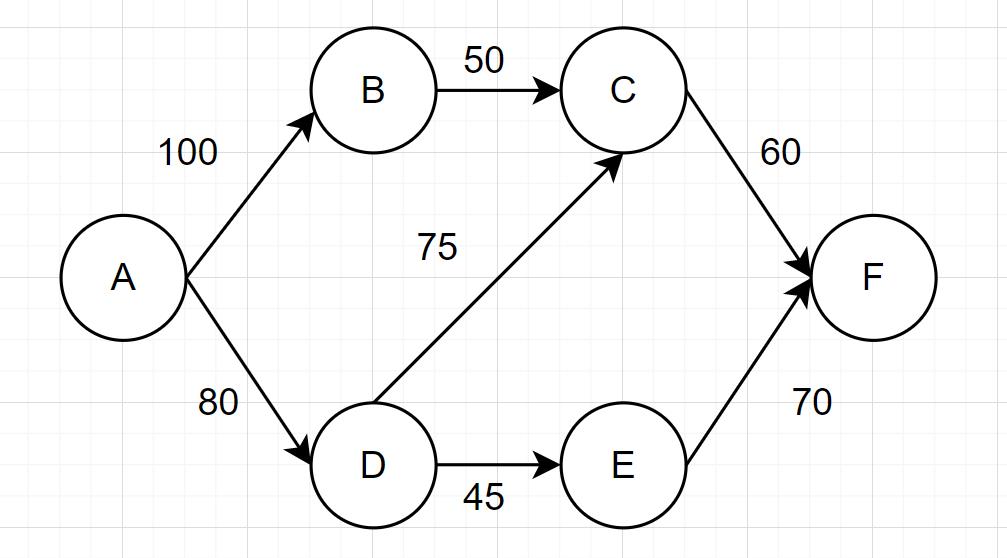
• AOE(Activity On Edge NetWork)图，以顶点表示事件，以有向边表示活动，以边上的权值表示该活动的持续时间。
• 工程开始的顶点称为源点，该点的入度为0，如A；工程结束的顶点称为汇点，该点的出度为0，如点F。
• 从源点到汇点的路径有多条，完成的事件有长短，且部分工作可以并行，那么拥有最长路径长度的路径影响了整个工程的完成时间，该路径称为关键路径，路径上的活动称为关键活动
• 每个活动有最早的开始时间，即该活动的前序活动都已完成；也有最晚开始时间，即后序活动要按时完成，该活动的必须开始时间。
• 对于最早开始时间和最迟开始时间相同的活动是重要的，不能拖延，否则会影响整个工程
• 则关键路径转换成求每个活动的最早开始时间和最晚开始时间。判断两个时间是否相同

算法步骤

1. 初始化拓扑排序的队列，初始化源点的最早开始时间
2. 进行拓扑排序，同时更新当前点相邻的所有点的最早开始时间
   earliest[v] = max(earliest[v], earliest[u] + l);,u为当前点,v为出度边的终点
3. 从拓扑序列的末尾开始遍历,计算最晚开始时间
   lastest[u] = min(lastest[u], lastest[v] - l);,u为当前点,v为出度边的终点
4. 遍历,最早开始时间等于最晚开始时间的活动为关键活动

例题

题目描述:
有一些指令存在依赖关系，且有些指令之间需要一定的安全距离，否则会导致错误。最常用的方法就是在两个指令之间添加空指令。两条指令之间的距离的定义是它们的开始的时间差。现在我们有一堆已知依赖和安全距离的指令，且有一个强大的CPU，可以并行任意多条指令，且任何指令只需要1ns就可执行完毕。请重新排列指令，使CPU可以使用最短的时间完成所有的指令。
输入描述：
每个输入有多个测试用例。
第一行有两个整数N，M（$N\le 1000,M\le 10000$）,有N个指令,M条独立的关系。
接下来的M行，每行有三个整数，X，Y，Z，表示X节点和Y节点之间的安全距离为Z，且Y需要在X之后运行。指令标号从0开始到N-1
输出描述：
输出一个整数,CPU需要的最短的运行时间

代码

注意点

• 可以很容易抽象出是一个关键路径的问题，但是需要注意每个指令的执行时间为1ns，所以所有源点的最早开始时间为1

#include <iostream>
#include <cstdio>
#include <vector>
#include <cstring>
#include <queue>
#include <climits>

using namespace std;

const int MAXN = 1001;
const int INF = INT_MAX;

struct Edge
{
    int to;
    int length;
    Edge(int t, int l) : to(t), length(l) {}
};

vector<Edge> graph[MAXN];
int earliest[MAXN];         //最早开始时间
int lastest[MAXN];          //最晚开始时间
int inDegree[MAXN];

void CriticalPath(int n)
{
    vector<int> topology;
    queue<int> node;
    for (int i = 0; i < n; i++)
    {
        if (inDegree[i] == 0)
        {
            node.push(i);
            earliest[i] = 1;            //初始化为1
        }
    }
    // 拓扑排序
    while (!node.empty())
    {
        int u = node.front();
        node.pop();
        topology.push_back(u);
        for (int i = 0; i < graph[u].size(); i++)
        {
            int v = graph[u][i].to;
            int l = graph[u][i].length;
            // 该活动最早的开始时间取决于前序所有活动最早的结束时间,即前序活动的最早开始时间+活动持续时间
            earliest[v] = max(earliest[v], earliest[u] + l);
            inDegree[v]--;
            if (inDegree[v] == 0)
                node.push(v);
        }
    }
    // 从拓扑序列的末尾开始遍历计算最晚开始时间
    for (int i = topology.size() - 1; i >= 0; i--)
    {
        int u = topology[i];
        // 如果该节点是汇点(graph[u].size()==该点的出度),则其最早开始时间等于其最晚开始时间,成为关键活动
        if (graph[u].size() == 0)
        {
            lastest[u] = earliest[u];
        }
        else
        {
            lastest[u] = INF;
        }
        // 对于非汇点,遍历其每一条出度边,也就是遍历其相邻的所有后序节点,计算最晚开始时间
        for (int j = 0; j < graph[u].size(); j++)
        {
            int v = graph[u][j].to;
            int l = graph[u][j].length;
            // 该节点的最晚开始时间为其后序节点中(最晚开始时间-活动持续时间)最小的那个值
            lastest[u] = min(lastest[u], lastest[v] - l);
        }
    }
}

int main(int argc, char const *argv[])
{
    int n, m;
    while (scanf("%d%d", &n, &m) != EOF)
    {
        memset(graph, 0, sizeof(graph));
        memset(earliest, 0, sizeof(earliest));
        memset(lastest, 0, sizeof(lastest));
        memset(inDegree, 0, sizeof(inDegree));
        while (m--)
        {
            int from, to, length;
            scanf("%d%d%d", &from, &to, &length);
            graph[from].push_back(Edge(to, length));
            inDegree[to]++;
        }
        CriticalPath(n);
        int answer = 0;
        for (int i = 0; i < n; i++)
        {
            answer = max(answer, earliest[i]);
        }
        printf("%d\\n", answer);
    }

    return 0;
}