卷积神经网络的卷积核大小如何确定呢？

Posted 2021-08-01 哦...

卷积神经网络的卷积核大小？答案是越小越好么?

本回答仅给出为何流行的DCNN通常采用小而深的卷积核。请看下面俩页PPT，可以给出一点启发。（出自海德堡大学HCI人工智能lecture）

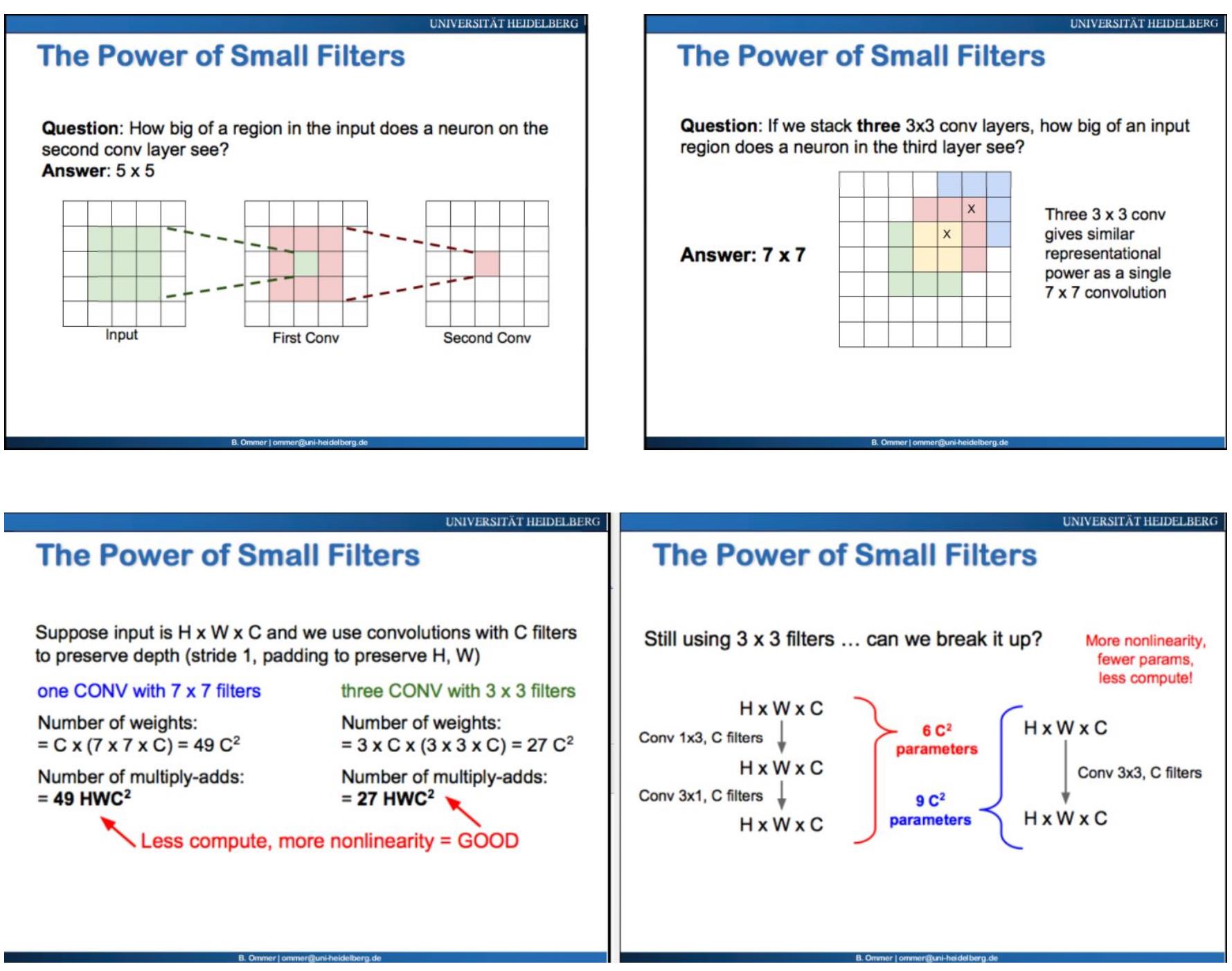
 上左图：假设卷积核（又叫filter，neuron）是3*3，第一层卷积核的中心pixel，可以“看到”（receptive field）输入图3*3的区域（这里把它理解成“连通性”），第二层卷积核作用在第一层之上，这个卷积核的中心pixel可以“看到”原图的区域扩大成5*5。

上右图：把三个3*3的卷积核堆积起来，第三层中的一个pixel，可以“看到”原图的pixel个数，和一个7*7卷积核一样。

下左图：但是计算复杂度，1个7*7卷积核的复杂度是49M（M是一个常数），三个3*3的复杂度是27M。

下右图：嫌3*3这个filter还不够小？那么再把它拆成俩个1*3的"向量”卷积核吧！结果是复杂度从9降到了6！

结论：几个小的卷积核（例如3*3）叠加（stack）在一起，相比一个大的卷积核（例如7*7），与原图的连通性不变，但是却大大降低了参数的个数以及计算复杂度！

一个直观的例子：

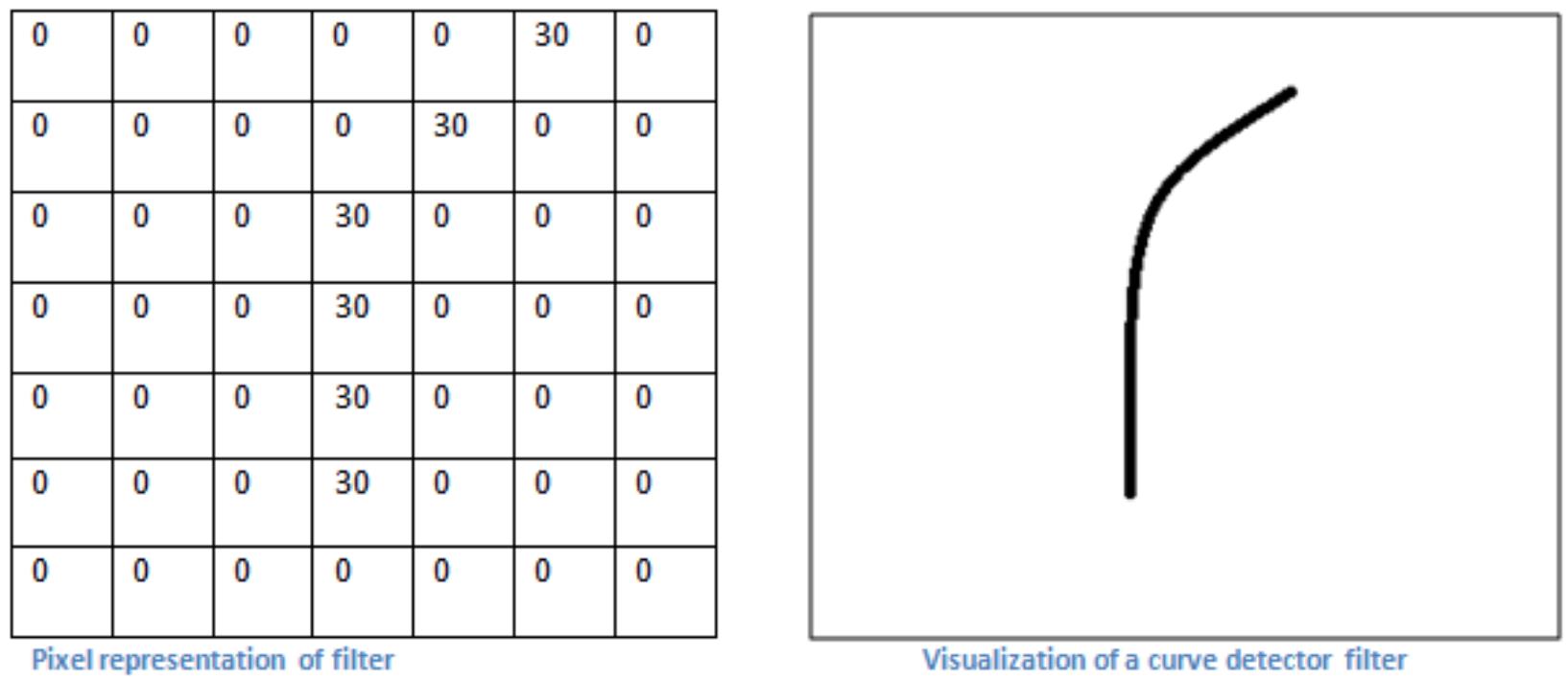
上图是一个7*7的卷积核（神经元），它可以刻画（识别）右图中的曲线(当输入图片出现右图中的模式时，这个神经元就会“放电”)。然而，由于空间太小，一个3*3的卷积核却表示不了。 搞三个3*3的叠加不就行了嘛！（把叠加想象成拼图，于是右图可以由三小块拼成）。

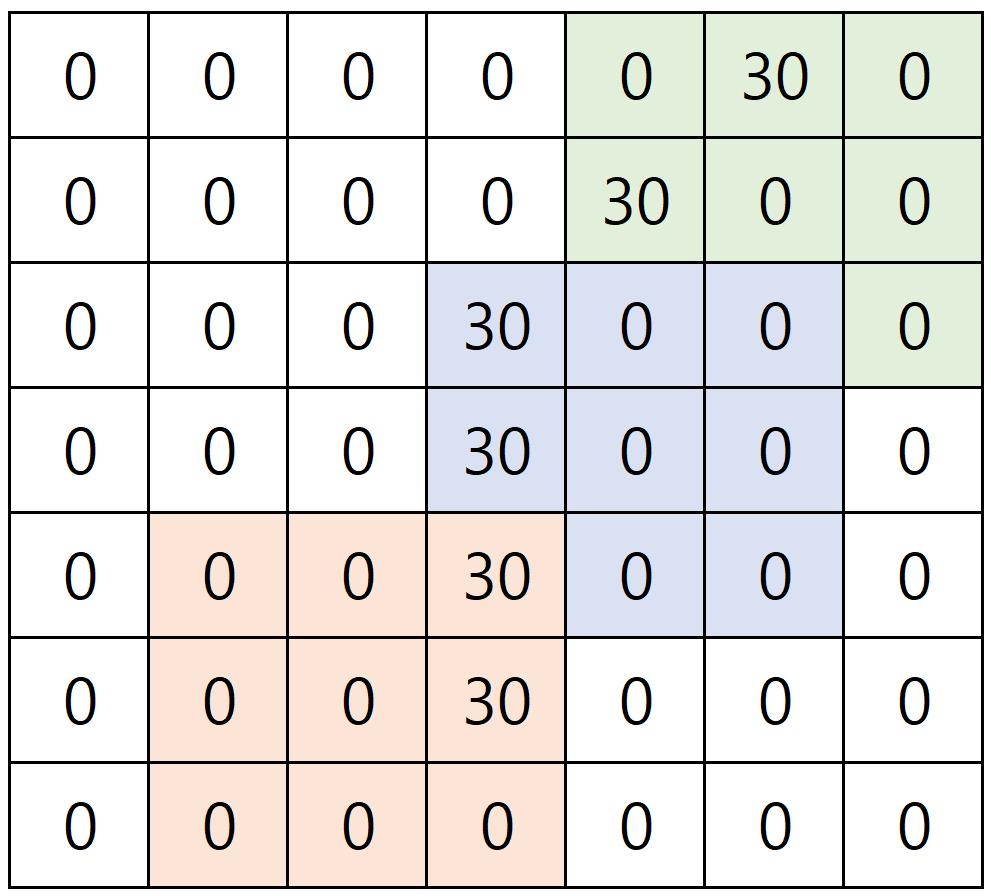
我们还可以搞个100*100的卷积核，它可以刻画几乎任何复杂的形状。但是，复杂度太太太高。或许搞20个3*3的叠加就可以复现上面的任何形状。

结论：这就是深度学习！

喜欢小而深，厌恶大而短（这里指的是卷积核大小和层数）。

另，如果输入图像是灰度图（高，宽），那么3*3的卷积核的shape也是(3,3)，20个卷积核会提取出图像的20个特征。如果输入图是彩色图，那么输入的内容就至少有3个通道，那么3*3的卷积核shape也是（3,3,3）。此时在提取特征图的运算过程如下图所示：

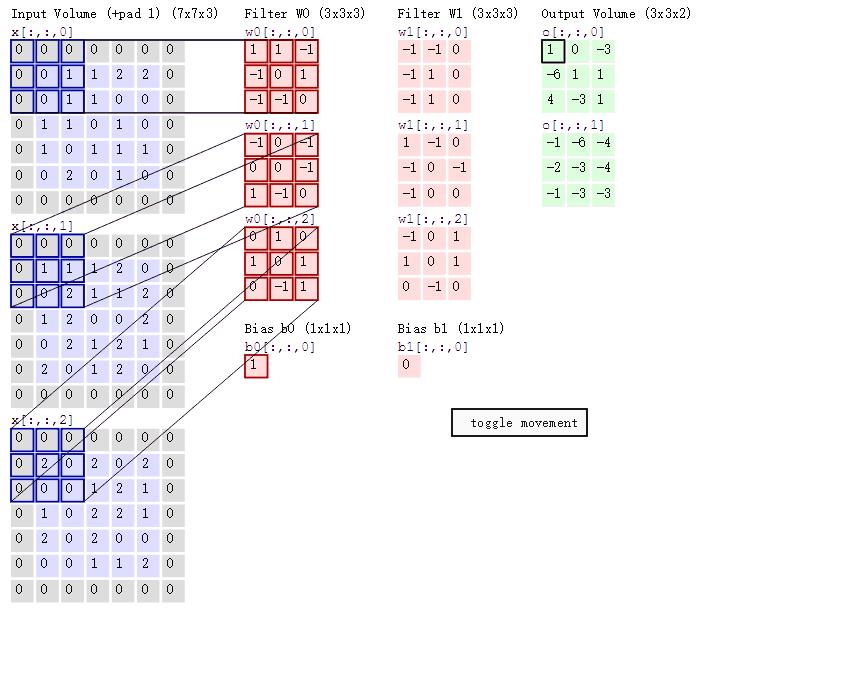
由w0过滤得到的特征图某位置（i,j）处的值，是由三个通道上（i,j）处的卷积结果相加得到。在有偏置的情况下，还要再加上偏置（w0有偏置1）。如果还有激活函数的话，还要将前面相加的结果经过一次激活函数的运算。图例中2个卷积核对输入层三通道内容进行提取后，得到了两个特征图。参数数量由输入层的7*7*3（宽*高*通道数量）变为了3*3*2（宽*高*特征图数量）。

上述过程再用一张形象的图来表示：

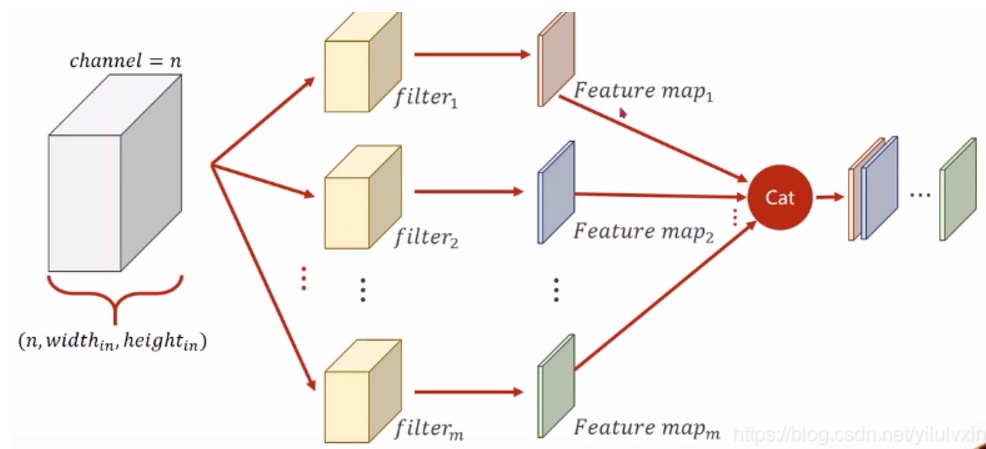
卷积过程中，输入层有多少个通道，卷积核就要有多少个通道。但卷积核的数量是任意的，卷积核的数量决定了卷积后的特征图数量。

本文参考了：

卷积神经网络的卷积核大小、卷积层数、每层map个数都是如何确定下来的呢？

多通道的多个卷积核