根据二叉树遍历结果重构二叉树(前序遍历+中序遍历 / 中序遍历+后序遍历 / LeetCode真题)

Posted 2021-07-31 Lotus_dong

文章目录

• • • 重构二叉树
    • • 前序遍历+中序遍历
      • 后序遍历+中序遍历
      • 前序遍历+后序遍历

重构二叉树

所谓重构二叉树就是根据遍历结果构造还原出原本的二叉树，在二叉树的四种遍历方法(前序遍历、中序遍历、后序遍历、层序遍历)中已经对二叉树的遍历进行了详细的分析，接下来我们就要分析如何根据不同的遍历结果重构出二叉树。

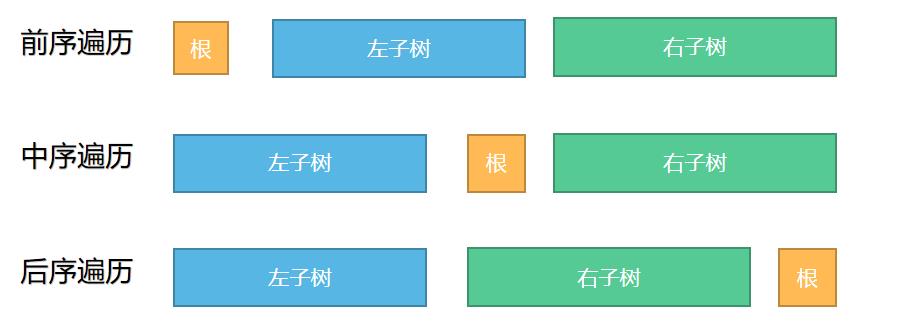
前序遍历的访问顺序：根节点——>前序遍历左子树——>前序遍历右子树

中序遍历的访问顺序：中序遍历左子树——>根节点——>中序遍历右子树

后序遍历的访问顺序：后序遍历左子树——>后序遍历右子树——>根节点

根据三种遍历的访问顺序，我们可以得到如下图关系：

前序遍历+中序遍历

由上图可知，我们每一次都可以根据前序遍历得到二叉树的根，并在中序遍历中通过根确定左子树和右子树，循环往复，就可以确定每一个元素在二叉树中的位置。

我们以LeetCode105题为例: 从前序与中序遍历序列构造二叉树

根据一棵树的前序遍历与中序遍历构造二叉树。

注意:
你可以假设树中没有重复的元素。

例如，给出

前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
返回如下的二叉树：

    3
   / \\
  9  20
    /  \\
   15   7

代码实现:

public TreeNode buildTree(int[] preorder, int[] inorder) {
        int preStart = 0;//假指针,指向preOrder
        int inStart = 0;//指向inorder
        int preEnd = preorder.length;//因为数组本身的操作比较麻烦,因此我们借用数组的长度来辅助作为终止指针
        int inEnd = inorder.length;
        return build(preorder, preStart,preEnd, inorder,inStart, inEnd);
    }

    private TreeNode build(int[] preorder,int preStart,int preEnd, int[] inorder,int inStart,int inEnd) {
        if (preStart == preEnd) {//前序遍历数组没有数据了就返回
            return null;
        }
        TreeNode root = new TreeNode(preorder[preStart]);
        //从中序遍历中寻找根节点的位置
        int index = inStart;
        for (int i = inStart; i < inEnd; i++) {
            if (preorder[preStart] == inorder[i]) {
                index = i;
                break;
            }
        }
        //左子树数量
        int leftNum = index - inStart;
        //为根节点添加左右子树
        root.left = build(preorder, preStart + 1, preStart+leftNum+1,
                inorder, inStart, index);
        root.right = build(preorder, preStart + leftNum + 1, preEnd,
                inorder, index + 1, inEnd);
        return root;
    }

后序遍历+中序遍历

和前序遍历相同，我们每一次都可以根据后序遍历得到二叉树的根，并在中序遍历中通过根确定左子树和右子树，循环往复，就可以确定每一个元素在二叉树中的位置。

我们以LeetCode106题为例: 从中序与后序遍历序列构造二叉树

根据一棵树的中序遍历与后序遍历构造二叉树。

注意:
你可以假设树中没有重复的元素。

例如，给出

中序遍历 inorder = [9,3,15,20,7]
后序遍历 postorder = [9,15,7,20,3]
返回如下的二叉树：

    3
   / \\
  9  20
    /  \\
   15   7

代码实现:

这个实现方法和上面的实现方法基本上是一样的,但这里我们使用HashMap将中序遍历的结果存储起来方便查找

int postEnd;
HashMap<Integer, Integer> map = new HashMap<>();

public TreeNode buildTree(int[] inorder, int[] postorder) {

    for (int i = 0; i < inorder.length; i++) {//将中序遍历结果存在map中,k为值,v为索引
        map.put(inorder[i], i);//作用是方便获取根节点
    }
    int inStart = 0;
    int inEnd = inorder.length-1;
    this.postEnd= postorder.length-1;
    return build(inorder, inStart, inEnd, postorder);
}

private TreeNode build(int[] inorder, int inStart, int inEnd,
                       int[] postorder) {
    if (inStart > inEnd) {
        return null;
    }
    //获取根节点
    TreeNode root = new TreeNode(postorder[postEnd]);
    //在中序遍历中拿到根节点所在的索引,区分左右子树
    int index = map.get(postorder[postEnd]);
    //postEnd减小
    postEnd--;
    //递归拿到左右子树
    root.right = build(inorder, index+1, inEnd,postorder);
    root.left = build(inorder, inStart,index-1,postorder);
    return root;
}

前序遍历+后序遍历

前序和后序遍历结果重构二叉树是有限制的，即二叉树必须是一颗真二叉树（度为1或0，就是要么左右节点都有，要么都没有），否则重构的结果不唯一。原因是当我们的二叉树缺少左子树和右子树时，我们只能确定根节点，不能确定剩下来的元素属于左子树还是右子树。