C语言数据结构(大话数据结构——笔记4)第六章:树
Posted Dontla
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了C语言数据结构(大话数据结构——笔记4)第六章:树相关的知识,希望对你有一定的参考价值。
文章目录
- 第六章:树(tree、root、subtree)(177)
- 树的定义(179)
- 结点分类(结点的度degree、叶结点leaf[终端结点]、分支结点[非终端节点]{内部结点}、树的度)(180)
- 结点间关系(结点的孩子child、孩子的双亲parent、结点的兄弟sibling、结点的祖先、结点的子孙)(180)
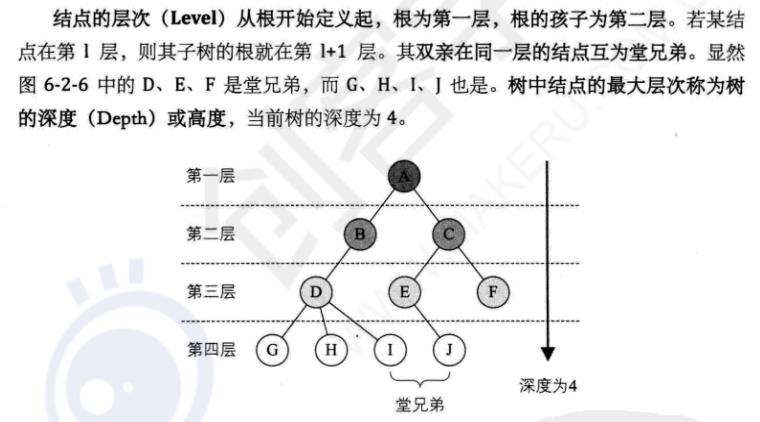
- 结点的层次level 树的深度{高度}depth 有序树、无序树 森林forest(181)
- 树结构与线性结构对比(182)
- 树的抽象数据类型(182)
- 树的存储结构(183)
- 二叉树(191)
- 二叉树的性质(197)
- 二叉树的顺序存储结构(200)
- 二叉树的链式存储(二叉链表)(201)
- 遍历二叉树(202)
- 二叉树的建立(215)
- 线索二叉树(216)
- 树、森林与二叉树的转换(223)
- 赫夫曼树(最优二叉树)及其应用(228)
- 第六章配套源码
第六章:树(tree、root、subtree)(177)
树的定义(179)

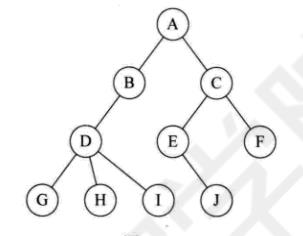

结点分类(结点的度degree、叶结点leaf[终端结点]、分支结点[非终端节点]{内部结点}、树的度)(180)
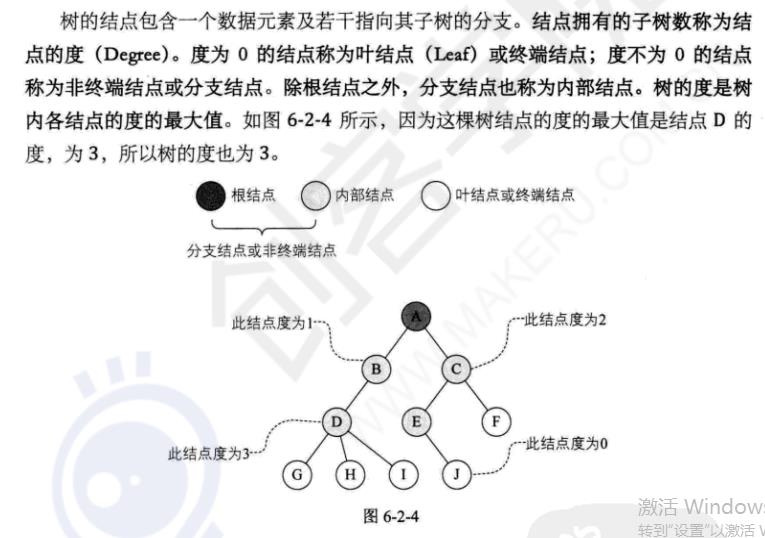
结点间关系(结点的孩子child、孩子的双亲parent、结点的兄弟sibling、结点的祖先、结点的子孙)(180)

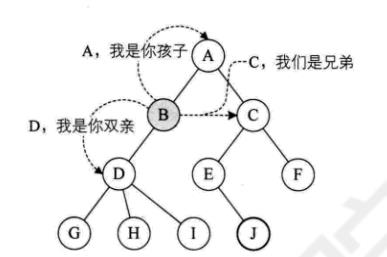
结点的层次level 树的深度{高度}depth 有序树、无序树 森林forest(181)

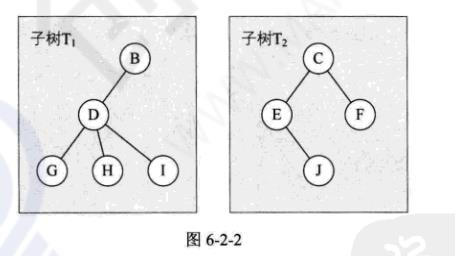
树结构与线性结构对比(182)

树的抽象数据类型(182)

树的存储结构(183)
双亲表示法(183)



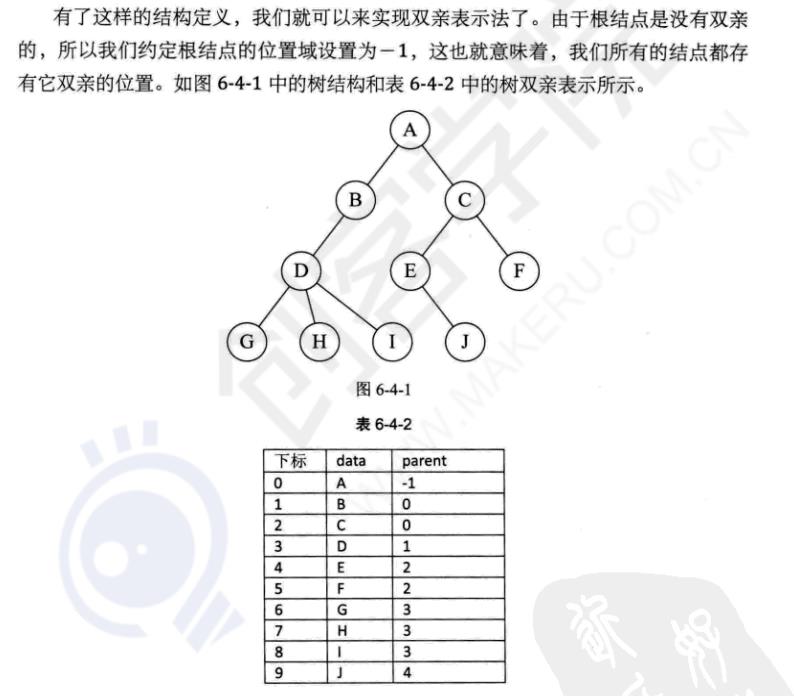

改良,增加长子域,但这样对于孩子大于两个,就不知道如何表示了(185)
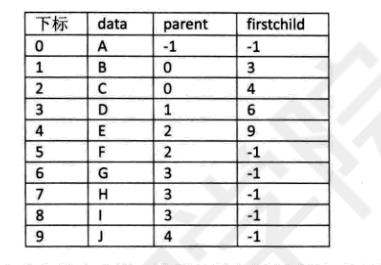
更关注兄弟,增加右兄弟域(185)
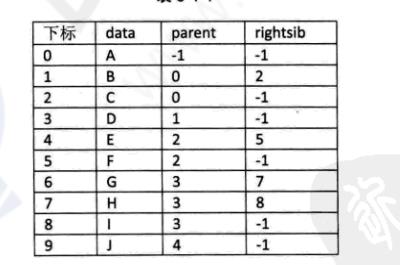
孩子表示法(186)
罗里吧嗦的,抓重点看!
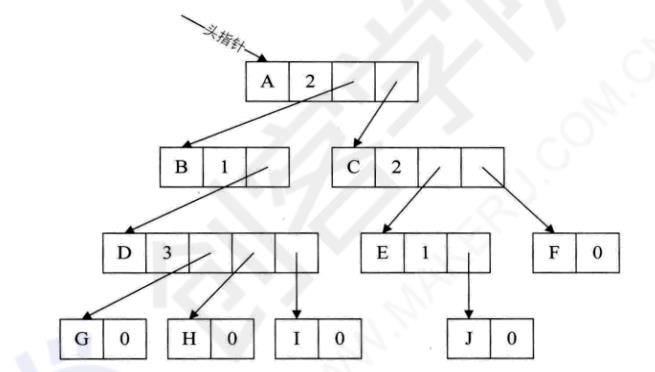

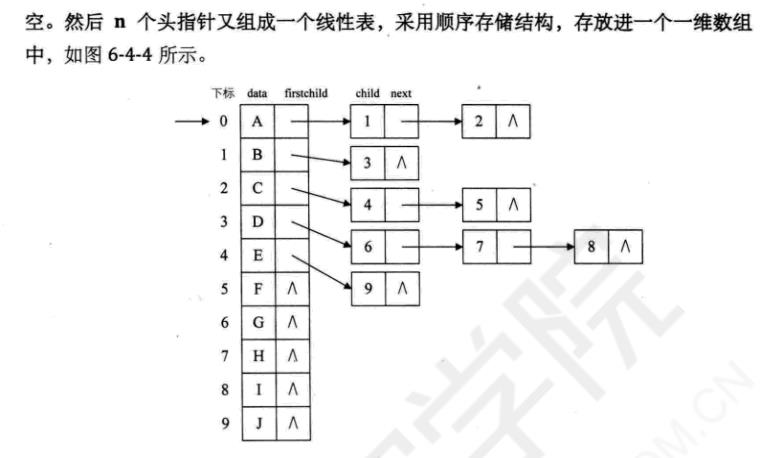



双亲孩子表示法(引出二叉树概念)(189)
但是这种方法不能知道结点的双亲是谁,可以改良一下:
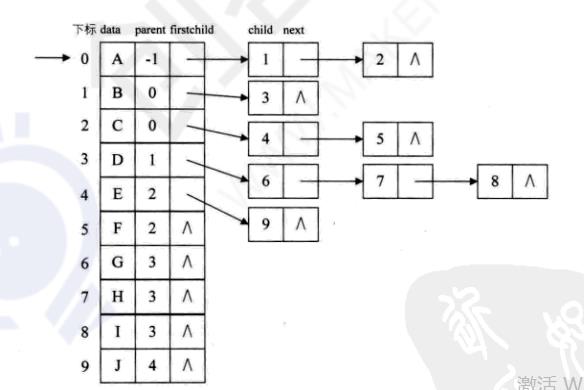
这种结构叫做“双亲孩子表示法”!
孩子兄弟表示法(190)


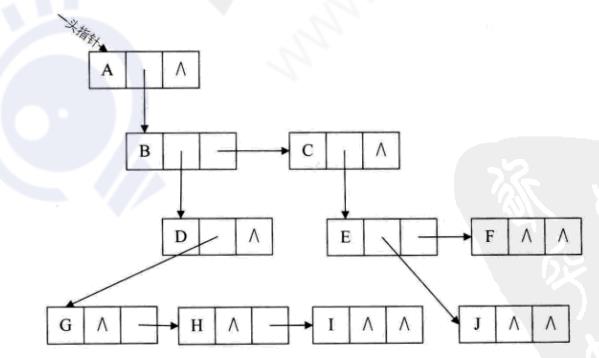
把上面这图变形(引出二叉树概念):
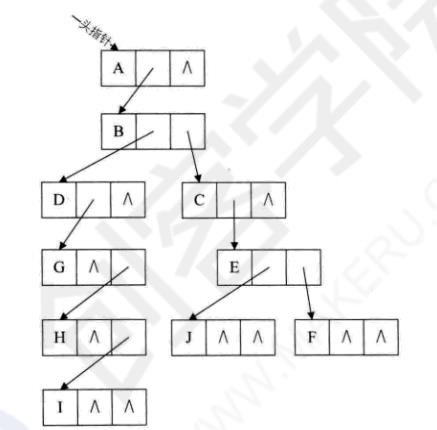
二叉树(191)

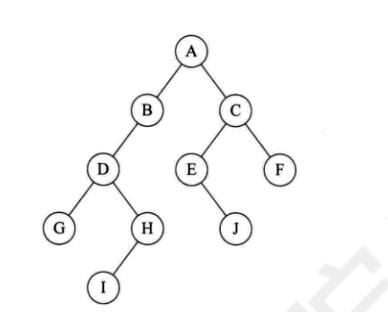
二叉树特点(五种基本形态)(193)
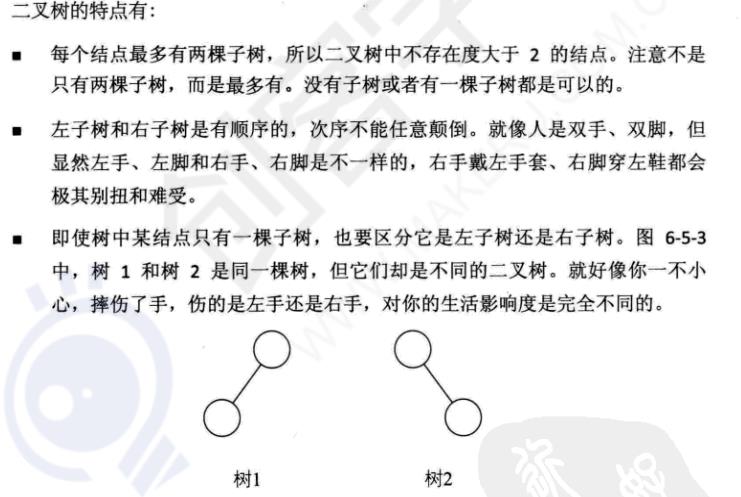
五种基本形态:
1、空二叉树
2、只有一个根结点
3、根结点只有左子树
4、根结点只有右子树
5、根结点既有左子树又有右子树
特殊二叉树(斜树、满二叉树、)(194)
斜树(线性表一种特殊结构的表示)(194)

满二叉树(195)
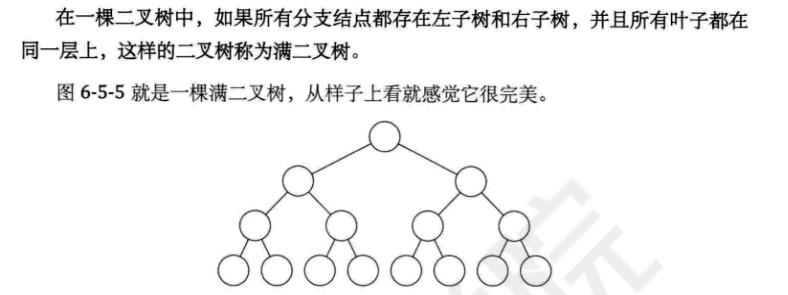

完全二叉树(195)
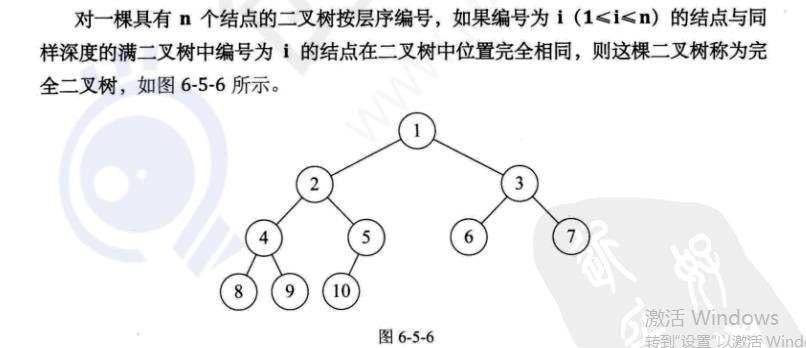
它的编号顺序都是从上到下,从左到右的,不能“空挡”,否则就不是完全二叉树了

二叉树的性质(197)



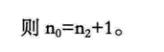



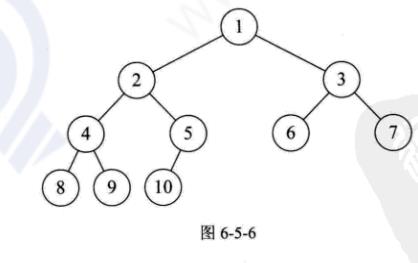
二叉树的顺序存储结构(200)
完全二叉树的存储
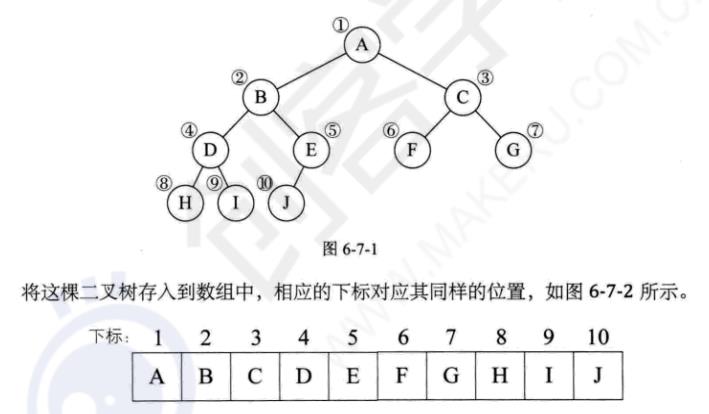
一般二叉树的存储
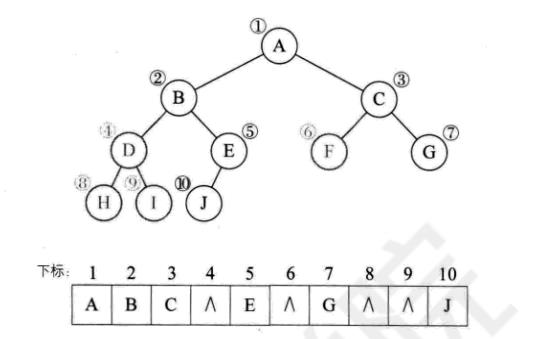
右斜树二叉树的存储
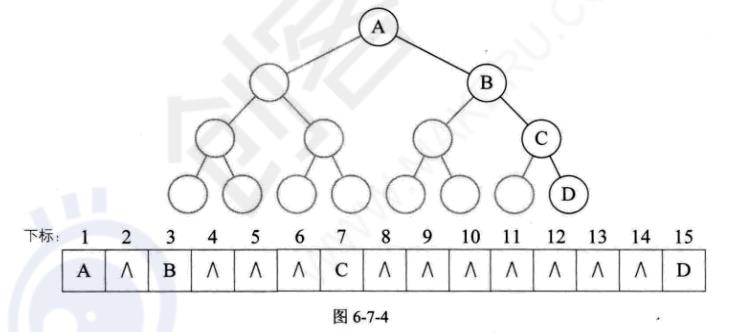
右斜树浪费空间,所以顺序存储结构一般只用于完全二叉树
二叉树的链式存储(二叉链表)(201)


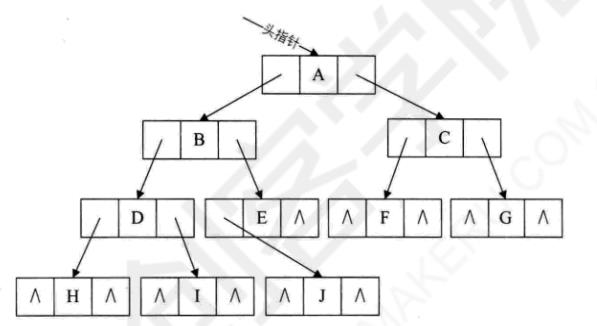
遍历二叉树(202)

前序遍历(203)

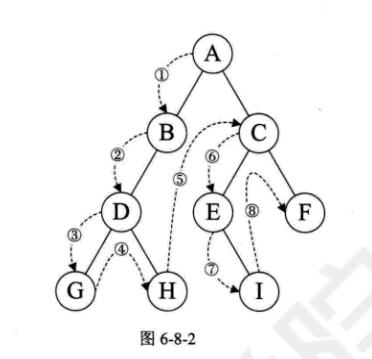
用栈保存中间结点?
中序遍历
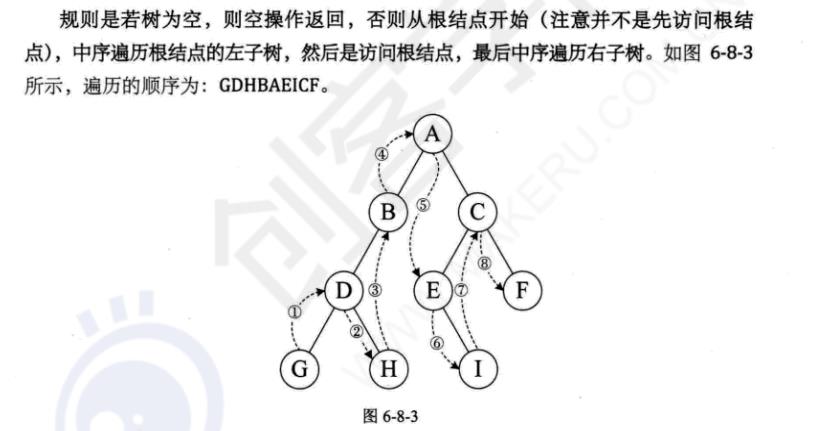
后序遍历

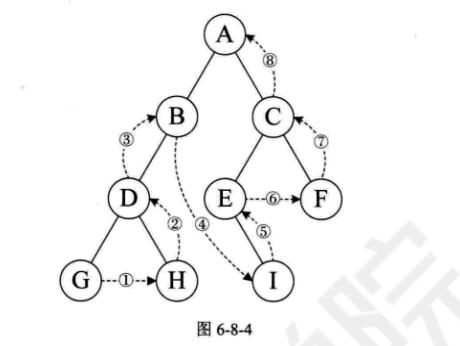
层序遍历(205)
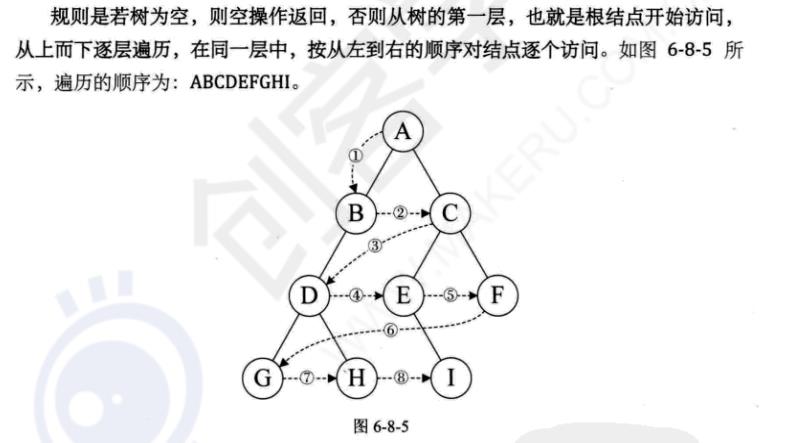
遍历算法(206)
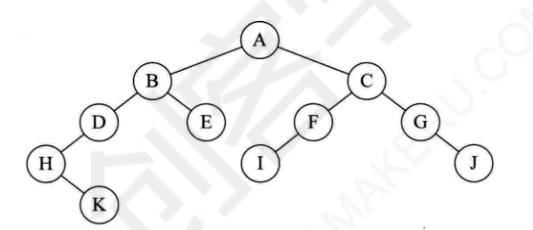
前序遍历算法(206)
递归算法

遍历结果:ABDHKECFIGJ
中序遍历算法(209)
就是在前序遍历算法顺序上调了个个

遍历结果:HKDBEAIFCGJ
后序遍历算法(212)

遍历结果:KHDEBIFJGCA
遍历推导结果(得出能够唯一确定二叉树的性质)(214)

二叉树的建立(215)
原二叉树的扩展二叉树(215)
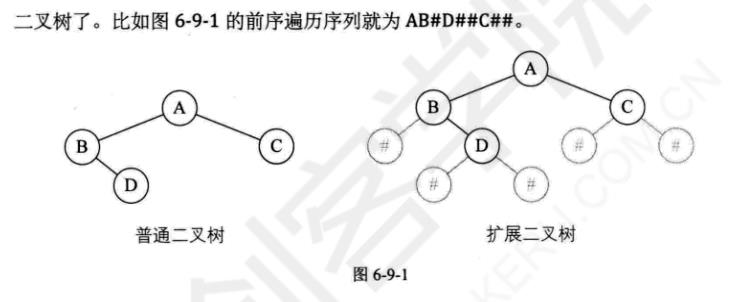
二叉树新建结点(前序)遍历结点代码



ps. 作者建立结构体的时候非得搞个什么附加命令,让人摸不着头脑,直接用二重指针表示它不香吗?
#include <stdio.h>
#include <stdlib.h>
#include <cstdlib>
//二叉链表结点
struct BiTNode
{
char data;
BiTNode* lchild;
BiTNode* rchild;
};
//新增结点
void CreateBiNode(BiTNode** A) {
char ch;
printf("请输入结点字符:\\n");
scanf_s("%c", &ch, sizeof(ch));
getchar();
if (ch == '#')
*A = NULL;
else
{
*A = (BiTNode*)malloc(sizeof(BiTNode));
if (!(*A))
exit(OVERFLOW);
(*A)->data = ch;
CreateBiNode(&((*A)->lchild));
CreateBiNode(&((*A)->rchild));
}
}
//前序遍历结点
void PreOrderTraverse(BiTNode* N) {
if (NULL == N) {
return;
}
printf("%c ", N->data);
PreOrderTraverse(N->lchild);
PreOrderTraverse(N->rchild);
printf("\\n");
}
int main() {
BiTNode* N;
//要把指向结点的指针的指针传进去才行,如果只是把指向结点的指针传进去是没有意义的,因为那个结点没初始化
CreateBiNode(&N);
PreOrderTraverse(N);
}
运行结果:
请输入结点字符:
a
请输入结点字符:
b
请输入结点字符:
c
请输入结点字符:
e
请输入结点字符:
d
请输入结点字符:
#
请输入结点字符:
#
请输入结点字符:
#
请输入结点字符:
#
请输入结点字符:
#
请输入结点字符:
#
a b c e d
线索二叉树(216)
指针域的空指针白白浪费空间
考虑在这些空指针的空间中存放指向前驱和后继的指针(217)

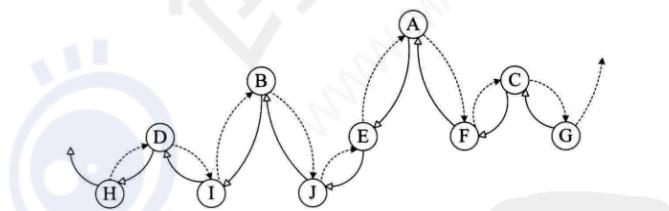


线索二叉树通过增加布尔变量标志位(存储量比指针地址小),来展示这是子孩还是前驱 | 后继
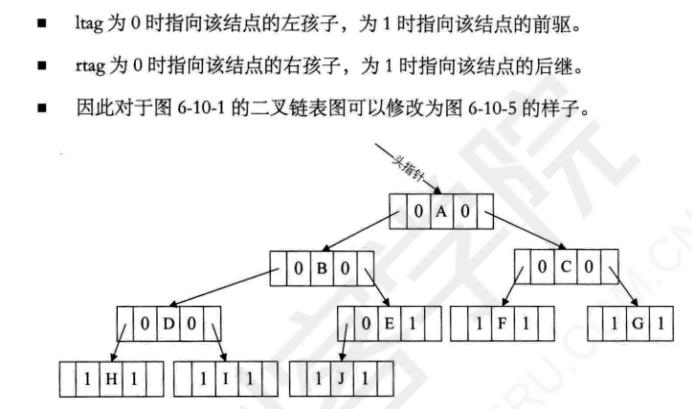
线索二叉树的实现(219)
创建




遍历


线索二叉树的好处:可以像双向链表那样操作(221)

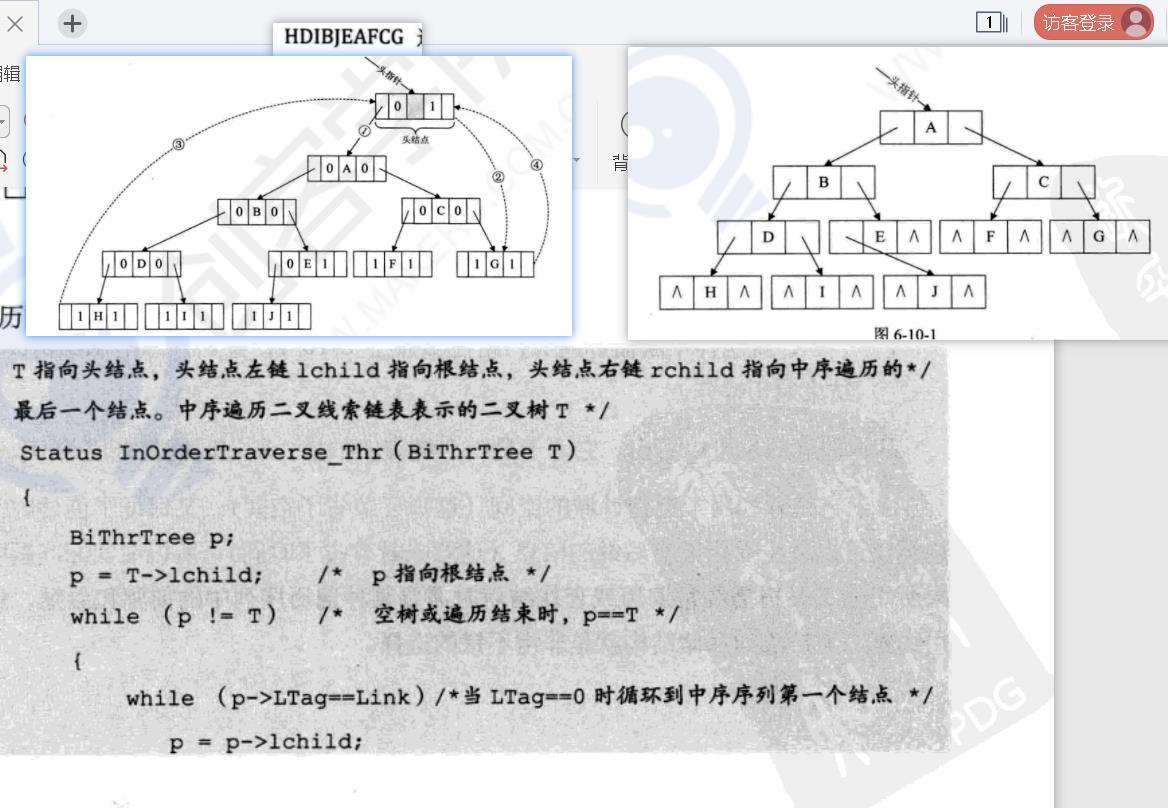
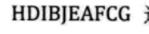
到A怎么到F?:A右标志位为0,直接就跳到C了

线索二叉树完整实现代码
#include "string.h"
#include "stdio.h"
#include "stdlib.h"
#include "io.h"
#include "math.h"
#include "time.h"
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 100 /* 存储空间初始分配量 */
typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */
typedef char TElemType;
typedef enum { Link, Thread } PointerTag; /* Link==0表示指向左右孩子指针, */
/* Thread==1表示指向前驱或后继的线索 */
typedef struct BiThrNode /* 二叉线索存储结点结构 */
{
TElemType data; /* 结点数据 */
struct BiThrNode* lchild, * rchild; /* 左右孩子指针 */
PointerTag LTag;
PointerTag RTag; /* 左右标志 */
} BiThrNode, * BiThrTree;
TElemType Nil = '#'; /* 字符型以空格符为空 */
Status visit(TElemType e)
{
printf("%c ", e);
return OK;
}
/* 按前序输入二叉线索树中结点的值,构造二叉线索树T */
/* 0(整型)/空格(字符型)表示空结点 */
Status CreateBiThrTree(BiThrTree* T)
{
TElemType h;
scanf_s("%c", &h, sizeof(h));
if (h == Nil)
*T = NULL;
else
{
*T = (BiThrTree)malloc(sizeof(BiThrNode));
if (!*T)
exit(OVERFLOW);
(*T)->data = h; /* 生成根结点(前序) */
CreateBiThrTree(&(*T)->lchild); /* 递归构造左子树 */
if ((*T)->lchild) /* 有左孩子 */
(*T)->LTag = Link;
CreateBiThrTree(&(*T)->rchild); /* 递归构造右子树 */
if ((*T)->rchild) /* 有右孩子 */
(*T)->RTag = Link;
}
return OK;
}
BiThrTree pre; /* 全局变量,始终指向刚刚访问过的结点 */
/* 中序遍历进行中序线索化 */
void InThreading(BiThrTree p)
{
if (p)
{
InThreading(p->lchild); /* 递归左子树线索化 */
if (!p->lchild) /* 没有左孩子 */
{
p->LTag = Thread; /* 前驱线索 */
p->lchild = pre; /* 左孩子指针指向前驱 */
}
if (!pre->rchild) /* 前驱没有右孩子 */
{
pre->RTag = Thread; /* 后继线索 */
pre->rchild = p; /* 前驱右孩子指针指向后继(当前结点p) */
}
pre = p; /* 保持pre指向p的前驱 */
InThreading(p->rchild); /* 递归右子树线索化 */
}
}
/* 中序遍历二叉树T,并将其中序线索化,Thrt指向头结点 */
Status InOrderThreading(BiThrTree* Thrt, BiThrTree T)
{
*Thrt = (BiThrTree)malloc(sizeof(BiThrNode));
if (!*Thrt)
exit(OVERFLOW);
(*Thrt)->LTag = Link; /* 建头结点 */
(*Thrt)->RTag = Thread;
(*Thrt)->rchild = (*Thrt); /* 右指针回指 */
if (!T) /* 若二叉树空,则左指针回指 */
(*Thrt)->lchild = *Thrt;
else
{
(*Thrt)->lchild = T;
pre = (*Thrt);
InThreading(T); /* 中序遍历进行中序线索化 */
pre->rchild = *Thrt;
pre->RTag = Thread; /* 最后一个结点线索化 */
(*Thrt)->rchild = pre;
}
return OK;
}
/* 中序遍历二叉线索树T(头结点)的非递归算法 */
Status InOrderTraverse_Thr(BiThrTree T)
{
BiThrTree p;
p = T->lchild; /* p指向根结点 */
while (p != T)
{ /* 空树或遍历结束时,p==T */
while (p->LTag == Link)
p = p->lchild;
if (!visit(p->data)) /* 访问其左子树为空的结点 */
return ERROR;
while (p->RTag == Thread && p->rchild != T)
{
p = p->rchild;
visit(p->data); /* 访问后继结点 */
}
p = p->rchild;
}
return OK;
}
int main()
{
BiThrTree H, T;
printf("请按前序输入二叉树(如:'ABDH##I##EJ###CF##G##')\\n");
CreateBiThrTree(&T); /* 按前序产生二叉树 */
InOrderThreading(&H, T); /* 中序遍历,并中序线索化二叉树 */
printf("中序遍历(输出)二叉线索树:\\n");
InOrderTraverse_Thr(H); /* 中序遍历(输出)二叉线索树 */
printf("\\n");
return 0;
}
运行结果:
请按前序输入二叉树(如:'ABDH##I##EJ###CF##G##')
ABDH##I##EJ###CF##G##
中序遍历(输出)二叉线索树:
H D I B J E A F C G
D:\\Dontla_small_project\\20210525_address_list\\cc++list\\dynamic_address_list\\Debug\\dynamic_address_list.exe (进程 31536) 已退出,代码为 0。
按任意键关闭此窗口. . .
树、森林与二叉树的转换(223)
树转换成二叉树(224)

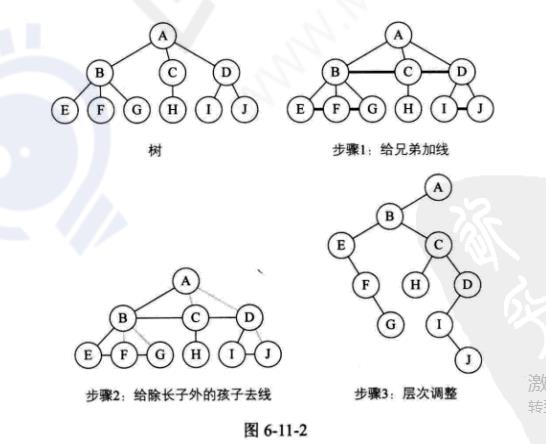
森林转换成二叉树(225)

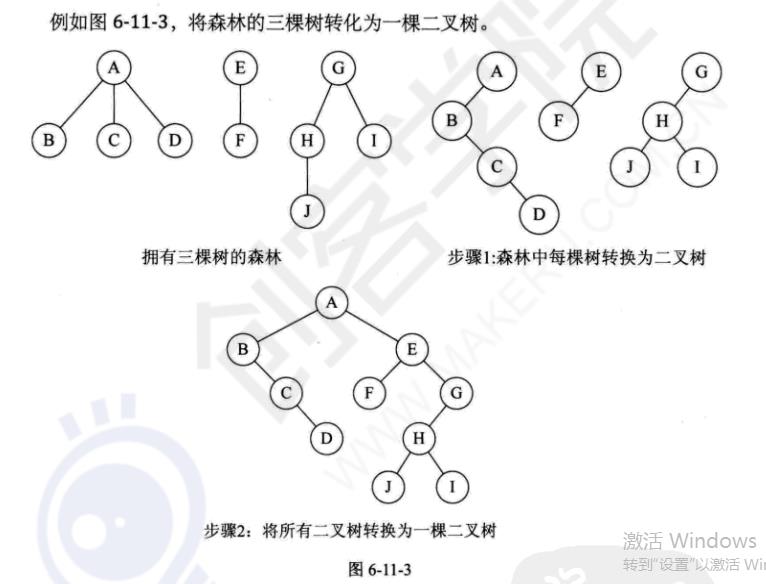
二叉树转化为树(225)

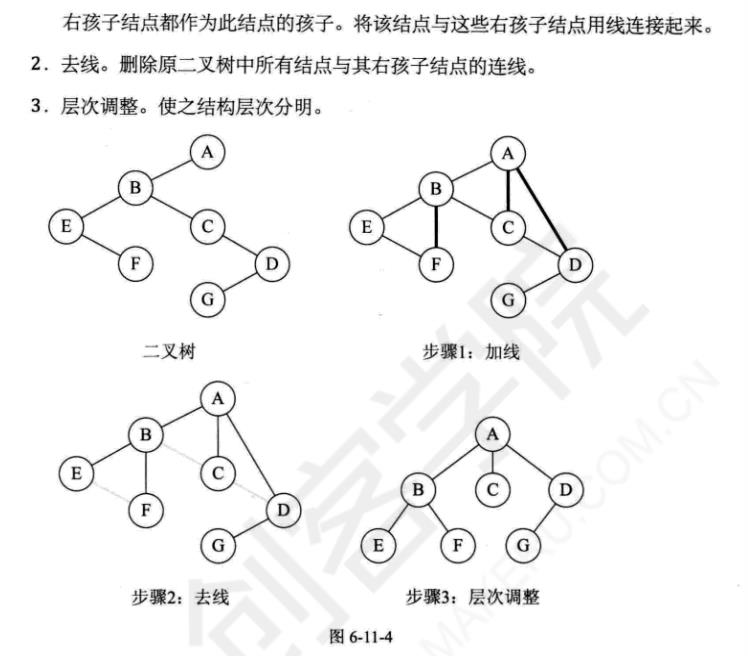
二叉树转换为森林(226)

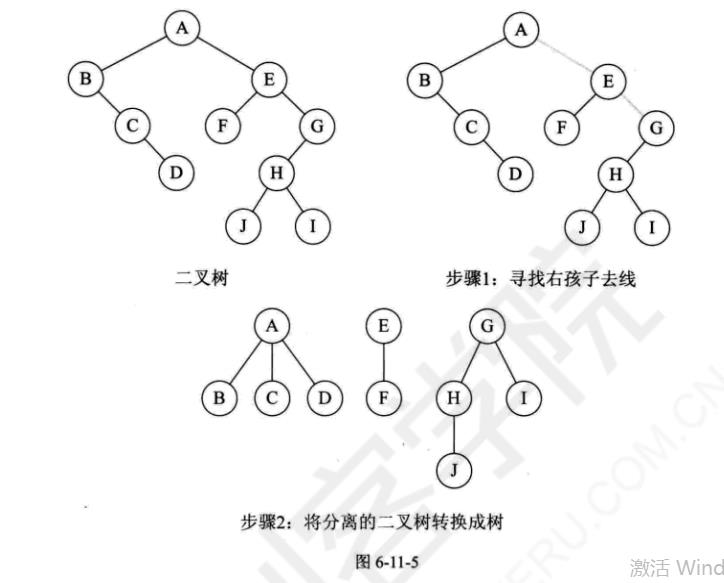
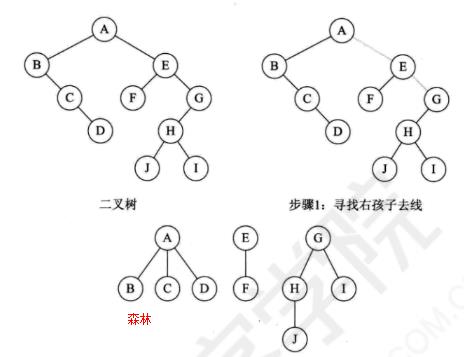
树与森林的遍历(结论:森林的前序遍历和二叉树的前序遍历结果相同,森林的后序遍历和二叉树的中序遍历结果相同)(227)

赫夫曼树(最优二叉树)及其应用(228)
赫夫曼树(赫夫曼编码)(228)
略
赫夫曼树的定义与原理(231)
路径长度

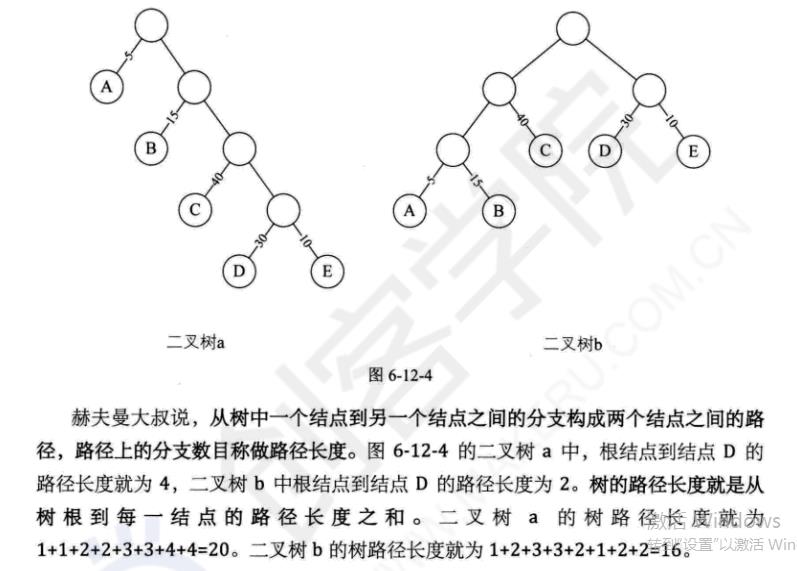
带权路径长度

赫夫曼树构建步骤(232)

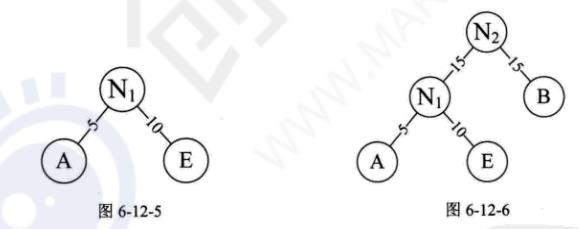
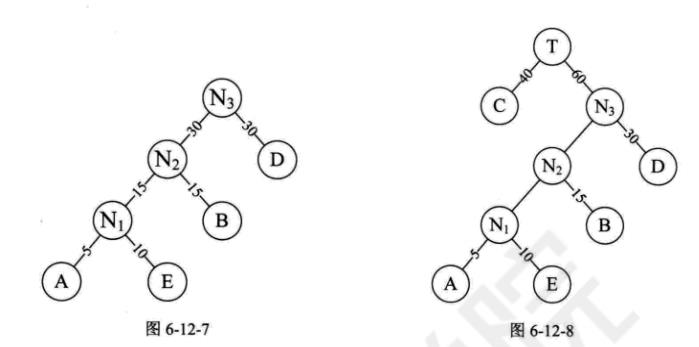
权值小的在左边
赫夫曼编码(233)
根据文本中字符出现的频次不同,可以将字符重新编码:
(原编码)

(赫夫曼编码)
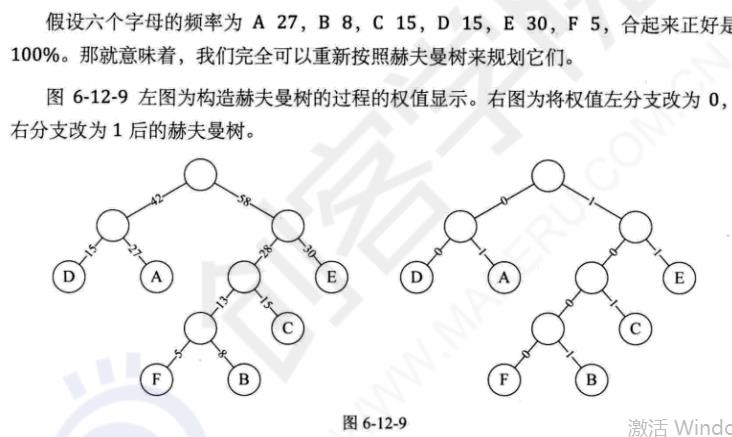
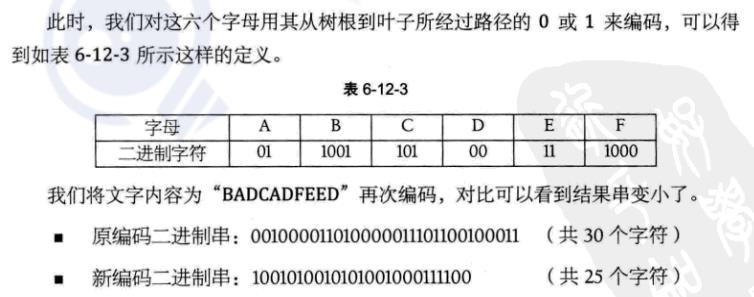
但是这种长短不一的编码该怎么解码呢?
前缀编码(235)



啥意思,看不懂。。。。
反正就是按照它约定的规则去解码,只能存在一种情况,没有多种情况啦!
构造霍夫曼编码的方法(235)

第六章配套源码
01二叉树顺序结构实现_BiTreeArray.cpp
#以上是关于C语言数据结构(大话数据结构——笔记4)第六章:树的主要内容,如果未能解决你的问题,请参考以下文章