小白必看的经典机器学习入门项目

Posted 2021-07-30 程序员石磊

1.股票预测

预测股市是机器学习在金融领域最重要的应用之一。在本文中，我将带您了解一个关于使用机器学习 Python 进行股票价格预测的简单数据科学项目。

在本文的最后，您将学习如何通过实现 Python 编程语言使用线性回归模型来预测股票价格。

自股市诞生以来，对其进行预测一直是投资者的祸根和目标。每天都有数十亿美元在股票交易所进行交易，每一美元背后都有一位投资者希望以某种方式获利。

整个公司每天的涨跌都取决于市场行为。如果一个投资者能够准确地预测市场走势，他就提供了一个诱人的财富和影响力的承诺。

1.1 数据准备

在上面的部分中，我通过导入python库开始了股票价格预测的任务。现在，我将编写一个函数来准备数据集，以便我们可以轻松地将其放入线性回归模型中:

def prepare_data(df,forecast_col,forecast_out,test_size):
    label = df[forecast_col].shift(-forecast_out) #creating new column called label with the last 5 rows are nan
    X = np.array(df[[forecast_col]]) #creating the feature array
    X = preprocessing.scale(X) #processing the feature array
    X_lately = X[-forecast_out:] #creating the column i want to use later in the predicting method
    X = X[:-forecast_out] # X that will contain the training and testing
    label.dropna(inplace=True) #dropping na values
    y = np.array(label)  # assigning Y
    X_train, X_test, Y_train, Y_test = train_test_split(X, y, test_size=test_size, random_state=0) #cross validation

    response = [X_train,X_test , Y_train, Y_test , X_lately]
    return response

df = pd.read_csv("prices.csv")
df = df[df.symbol == "GOOG"]

现在，我们需要准备三个输入变量，就像上面小节中创建的函数中准备的那样。我们需要声明一个输入变量，说明我们想预测哪一列。我们需要声明的下一个变量是我们希望预测的距离。

我们需要声明的最后一个变量是测试集的大小应该是多少。现在让我们声明所有的变量:

1.2 将机器学习应用于股票价格预测

现在我将对数据进行分割，并拟合到线性回归模型中:

X_train, X_test, Y_train, Y_test , X_lately =prepare_data(df,forecast_col,forecast_out,test_size); #calling the method were the cross validation and data preperation is in
learner = LinearRegression() #initializing linear regression model

learner.fit(X_train,Y_train) #training the linear regression model

现在让我们预测产出，看看股票价格的价格:

score=learner.score(X_test,Y_test)#testing the linear regression model
forecast= learner.predict(X_lately) #set that will contain the forecasted data
response={}#creting json object
response['test_score']=score
response['forecast_set']=forecast

print(response)

{‘test_score’: 0.9481024935723803, ‘forecast_set’: array([786.54352516, 788.13020371, 781.84159626, 779.65508615, 769.04187979])}

2.美国总统身高统计

如果你是数据科学的初学者，你必须解决这个项目，因为你将学到很多关于处理来自csv文件或任何其他格式的数据的知识。

该数据可在文件height.Csv中找到，它是标签和值的简单逗号分隔列表:

链接：https://pan.baidu.com/s/1tW-3TBzCzyeX1U2vtdEhFw
提取码：qz25

data = pd.read_csv("heights.csv")
print(data.head())

我们将使用Pandas package 读取文件并提取此信息 (请注意，高度以厘米为单位):

height = np.array(data["height(cm)"])
print(height)

现在我们有了这个数据数组，我们可以计算各种摘要统计信息:

print("Mean of heights =", height.mean())
print("Standard Deviation of height =", height.std())
print("Minimum height =", height.min())
print("Maximum height =", height.max())

请注意，在每种情况下，聚合操作将整个数组简化为一个汇总值，这为我们提供了有关值分布的信息。我们也可以计算分位数:

print("25th percentile =", np.percentile(height, 25))
print("Median =", np.median(height))
print("75th percentile =", np.percentile(height, 75))

我们看到美国总统的平均身高是182厘米，或略低于6英尺。当然，有时查看这些数据的可视化表示会更有用，我们可以使用Matplotlib中的工具来完成:

import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
plt.hist(height)
plt.title("Height Distribution of Presidents of USA")
plt.xlabel("height(cm)")
plt.ylabel("Number")
plt.show()

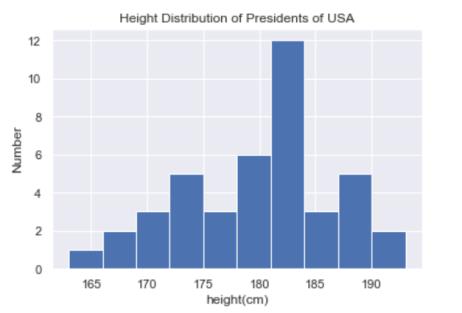
这些集合是探索性数据科学的一些基本部分，我们将在以后的项目中更深入地探讨。

3.出生率分析

让我们来看看美国疾病控制中心 (CDC) 提供的免费出生数据。这些数据可以在born s.csv中找到

链接：https://pan.baidu.com/s/1lrCuMvGGqtxfmuVHocZCpA
提取码：8ovj

import pandas as pd
births = pd.read_csv("births.csv") print(births.head()) births['day'].fillna(0, inplace=True) births['day'] = births['day'].astype(int)

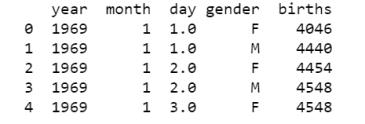
births['decade'] = 10 * (births['year'] // 10)
births.pivot_table('births', index='decade', columns='gender', aggfunc='sum')
print(births.head())

我们立即看到，每十年男性出生数超过女性出生数。为了更清楚地看到这一趋势，我们可以使用Pandas 中的内置绘图工具来可视化按年出生的总数:

import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
birth_decade = births.pivot_table('births', index='decade', columns='gender', aggfunc='sum')
birth_decade.plot()
plt.ylabel("Total births per year")
plt.show()

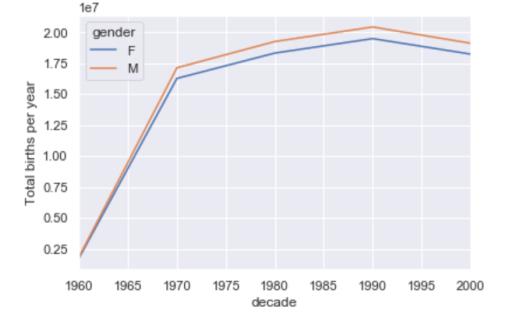
3.1 进一步数据探索:

这里有一些有趣的特性，我们可以使用Pandas工具从这个数据集中提取出来。我们必须从清理数据开始，删除由于输入错误的日期或丢失的值而引起的异常值。一个简单的方法是一次性删除这些异常值，我们将通过一个健壮的sigma-clipping操作来做到这一点:

import numpy as np
quartiles = np.percentile(births['births'], [25, 50, 75])
mu = quartiles[1]
sig = 0.74 * (quartiles[2] - quartiles[0])

最后这条线是样本均值的稳健估计，其中0.74来自高斯分布的四分位数范围。这样我们就可以使用query()方法来过滤出这些值之外的诞生行:

births = births.query('(births > @mu - 5 * @sig) & (births < @mu + 5 * @sig)')
births['day'] = births['day'].astype(int)
births.index = pd.to_datetime(10000 * births.year +
                              100 * births.month +
                              births.day, format='%Y%m%d')

births['dayofweek'] = births.index.dayofweek

利用这个数据，我们可以连续几十年按工作日计算出生人数:

births.pivot_table('births', index='dayofweek',
                    columns='decade', aggfunc='mean').plot()
plt.gca().set_xticklabels(['Mon', 'Tues', 'Wed', 'Thurs', 'Fri', 'Sat', 'Sun'])
plt.ylabel('mean births by day');
plt.show()

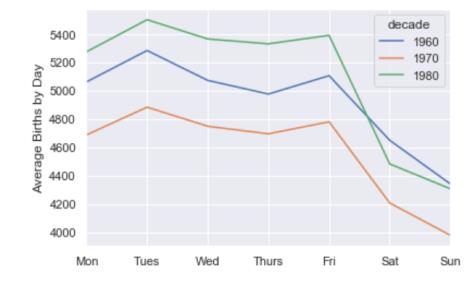
显然，周末出生的孩子比工作日出生的要少一些!需要注意的是，由于CDC的数据只包含了从1989年开始的出生月份，所以没有包括1990年代和2000年代。
另一个有趣的观点是画出每年的平均出生人数。让我们首先将数据按月和日分别分组:

births_month = births.pivot_table('births', [births.index.month, births.index.day])
print(births_month.head())
births_month.index = [pd.datetime(2012, month, day)
for (month, day) in births_month.index]
print(births_month.head())

只关注月和日，我们现在有了一个时间序列，反映了每年出生的平均人数。由此，我们可以使用plot方法来绘制数据。它揭示了一些有趣的趋势:

fig, ax = plt.subplots(figsize=(12, 4))
births_month.plot(ax=ax)
plt.show()

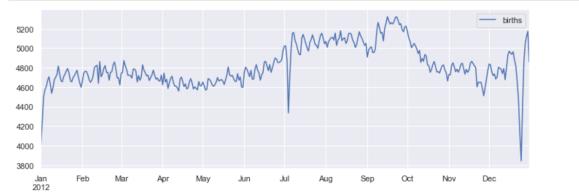
4.时间序列数据科学项目-自行车计数

作为处理时间序列数据的一个例子，让我们看看西雅图弗里蒙特桥上的自行车数量。这些数据来自于2012年底安装的一个自动自行车计数器，它在大桥的东西两侧人行道上安装了感应传感器。每小时的自行车计数可以在这里下载。

一旦下载了这个数据集，我们就可以使用Pandas将CSV输出读取到一个DataFrame中。我们将指定我们想要的日期作为索引，并且我们想要这些日期被自动解析:

import pandas as pd
data = pd.read_csv("fremont-bridge.csv", index_col= 'Date', parse_dates=True)
data.head()

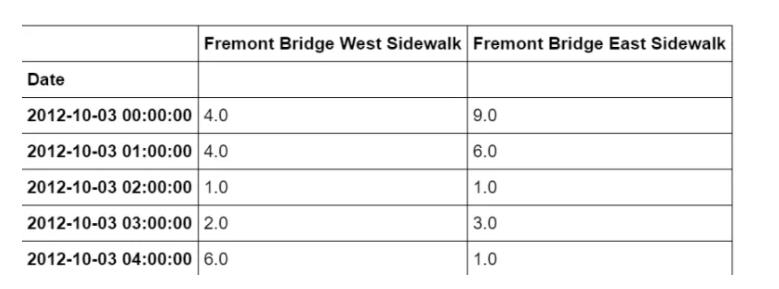
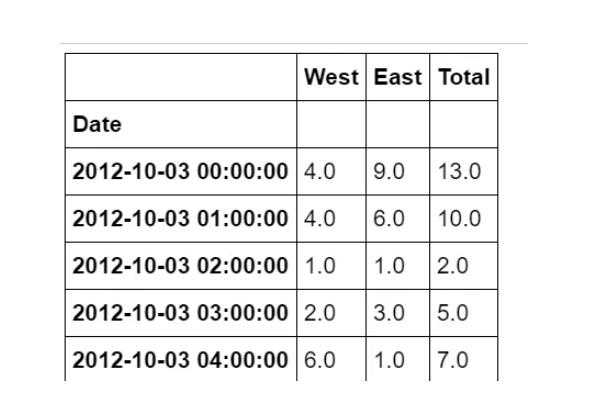
为方便起见，我们将通过缩短列名并添加 “总计” 列来进一步处理此数据集:

data.columns = ["West", "East"]
data["Total"] = data["West"] + data["East"]
data.head()

现在，让我们看一下此数据的摘要统计信息:

data.dropna().describe()

4.1 可视化数据

我们可以通过可视化来深入了解数据集。让我们从绘制原始数据开始:

import matplotlib.pyplot as plt
import seaborn
seaborn.set()
data.plot()
plt.ylabel("Hourly Bicycle count")
plt.show()

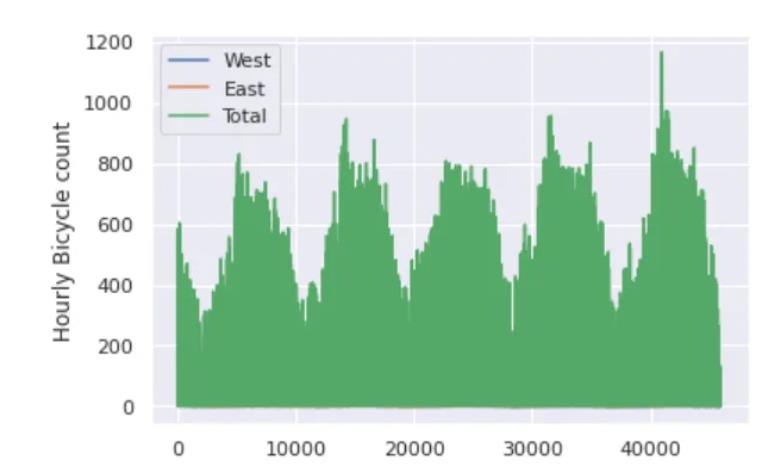
每小时约25000个样本的密度太大了，我们无法理解。我们可以通过将数据重新采样到一个粗糙的网格来获得更多的见解。让我们按周重新取样:

weekly = data.resample("W").sum()
weekly.plot(style=[':', '--', '-'])
plt.ylabel('Weekly bicycle count')
plt.show()

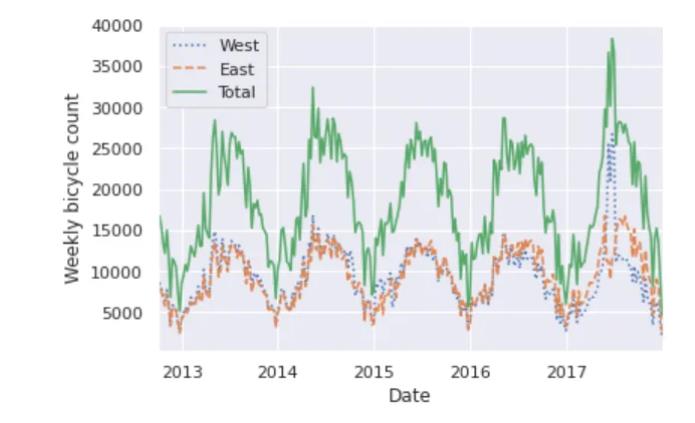
这向我们展示了一些有趣的季节趋势:如你所料，人们在夏天比在冬天骑自行车更多，甚至在一个特定的季节里，自行车的使用每周都不同。

另一种便于聚合数据的方法是使用滚动平均数，利用pd.rolling_mean()函数。这里我们将对我们的数据做一个30天的滚动平均值，确保窗口居中:

daily = data.resample('D').sum()
daily.rolling(30, center=True).sum().plot(style=[':', '--', '-'])
plt.ylabel('mean hourly count')
plt.show()

结果的锯齿状是由于窗户的硬切断。我们可以使用窗口函数得到滚动均值的平滑版本——例如高斯窗。

daily.rolling(50, center=True,
win_type='gaussian').sum(std=10).plot(style=[':','--', '-'])
plt.show()

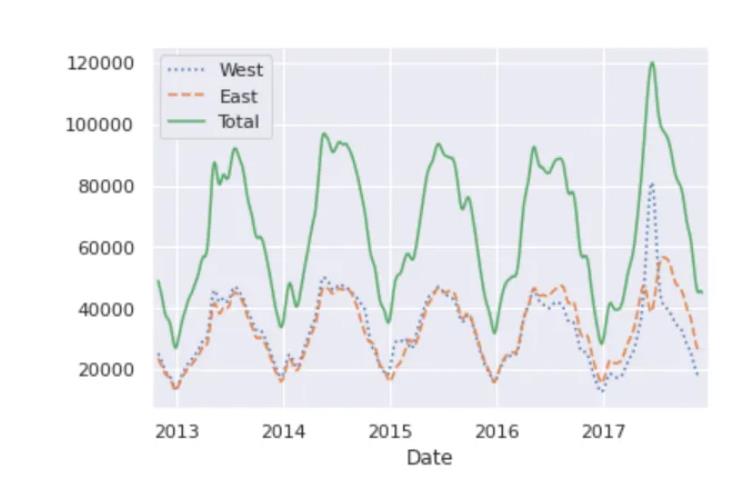
4.2 挖掘数据

虽然平滑数据视图有助于了解数据的总体趋势，但它们隐藏了许多有趣的结构。例如，我们可能希望将平均流量看作是一天中时间的函数。我们可以使用GroupBy功能来做到这一点:

import numpy as np
by_time = data.groupby(data.index.time).mean()
hourly_ticks = 4  60  60 * np.arange(6)
by_time.plot(xticks= hourly_ticks, style=[':', '--', '-'])
plt.ylabel("Traffic according to time")
plt.show()

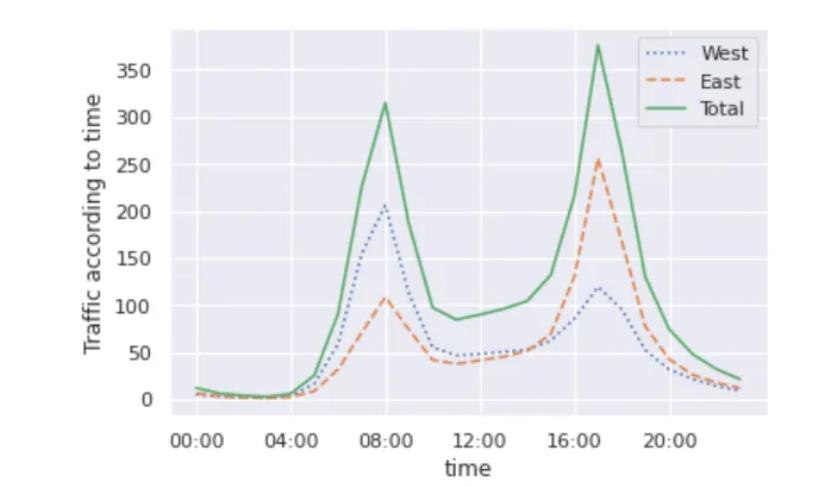
5.区域与人口分析

在这个项目中，我们将使用点的大小来指示加利福尼亚城市的面积和人口。我们想要一个指定点大小比例的图例，我们将通过绘制一些没有条目的标记数据来实现这一点。

您可以从此处下载此项目所需的数据集。

链接：https://pan.baidu.com/s/1_KoQ7zTT8fJpRYrxksr0aQ
提取码：guqw

import pandas as pd
cities = pd.read_csv("california_cities.csv")
print(cities.head())

5.1 提取我们感兴趣的数据

latitude, longitude = cities["latd"], cities["longd"]
population, area = cities["population_total"], cities["area_total_km2"]

5.2 分散点，使用尺寸和颜色，但不使用标签

import numpy as np
import matplotlib.pyplot as plt
import seaborn
seaborn.set()
plt.scatter(longitude, latitude, label=None, c=np.log10(population),
cmap='viridis', s=area, linewidth=0, alpha=0.5)
plt.axis(aspect='equal')
plt.xlabel('Longitude')
plt.ylabel('Longitude')
plt.colorbar(label='log(population)')
plt.clim(3, 7)

5.3 现在我们将创建一个图例，我们将绘制具有所需大小和标签的空列表

for area in [100, 300, 500]:
plt.scatter([], [], c='k', alpha=0.3, s=area, label=str(area) + 'km')
plt.legend(scatterpoints=1, frameon=False, labelspacing=1, title='City Areas')
plt.title("Area and Population of California Cities")
plt.show()

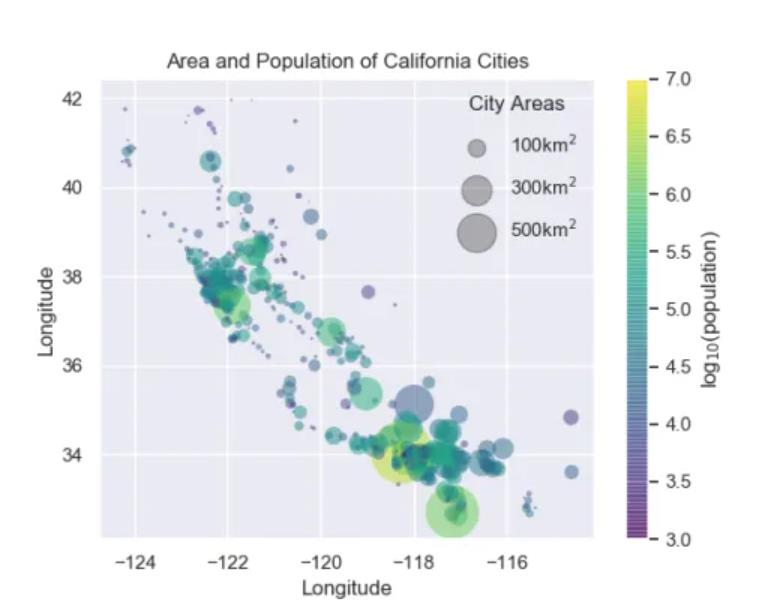
6.一个完整的Python机器学习项目实战

在本文中，我将带您完成一个使用Python编程语言的完整机器学习项目演练。这个完整的机器学习项目演练包括由Scikit-Learn提供的算法的实现，Scikit-Learn是用于机器学习的最佳Python库之一。

以下是本机器学习项目演练中涵盖的步骤:

1. 导入数据
2. 数据可视化
3. 数据清理和转换
4. 对数据进行编码
5. 将数据拆分为训练和测试集
6. 微调算法
7. 使用KFold交叉验证
8. 对测试集的预测

使用Python的机器学习项目演练

现在，在本节中，我将带您完成一个使用Python编程语言的完整机器学习项目演练。我将首先导入必要的Python库和数据集:

链接：https://pan.baidu.com/s/1ShfQd-ig8JhLqwigxfP_-g
提取码：3zgw

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
data_train = pd.read_csv('train.csv')
data_test = pd.read_csv('test.csv')

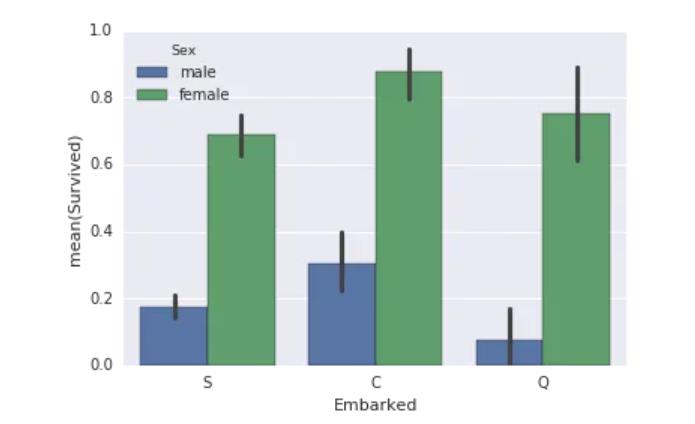
现在让我们看看如何可视化这些数据。数据可视化对于识别适当训练机器学习模型的基础模式至关重要:

sns.barplot(x="Embarked", y="Survived", hue="Sex", data=data_train)
plt.show()

6.1 数据清理和转换

现在下一步是根据我们需要的输出来清理和转换数据。以下是我将在此步骤中考虑的步骤:

1. 为了避免过度匹配，我将把人们分成合乎逻辑的人类年龄组。
2. 每个展位都以一封信开头。我打赌这封信比后面的数字大得多，让我们把它剪掉。
3. 关税是另一个应该简化的连续值。
4. 从 “名称” 函数中提取信息。我没有使用全名，而是提取了姓氏和名字前缀 (Mr，Mrs等)，然后将它们添加为特征。
5. 最后，我们需要删除不必要的功能。

def simplify_ages(df):
df.Age = df.Age.fillna(-0.5)
bins = (-1, 0, 5, 12, 18, 25, 35, 60, 120)
group_names = ['Unknown', 'Baby', 'Child', 'Teenager', 'Student', 'Young Adult', 'Adult', 'Senior']
categories = pd.cut(df.Age, bins, labels=group_names)
df.Age = categories
return df
def simplify_cabins(df):
df.Cabin = df.Cabin.fillna('N')
df.Cabin = df.Cabin.apply(lambda x: x[0])
return df
def simplify_fares(df):
df.Fare = df.Fare.fillna(-0.5)
bins = (-1, 0, 8, 15, 31, 1000)
group_names = ['Unknown', '1_quartile', '2_quartile', '3_quartile', '4_quartile']
categories = pd.cut(df.Fare, bins, labels=group_names)
df.Fare = categories
return df
def format_name(df):
df['Lname'] = df.Name.apply(lambda x: x.split(' ')[0])
df['NamePrefix'] = df.Name.apply(lambda x: x.split(' ')[1])
return df
def drop_features(df):
return df.drop(['Ticket', 'Name', 'Embarked'], axis=1)
def transform_features(df):
df = simplify_ages(df)
df = simplify_cabins(df)
df = simplify_fares(df)
df = format_name(df)
df = drop_features(df)
return df
data_train = transform_features(data_train)
data_test = transform_features(data_test)

6.2 编码特征

下一步是标准化标签。标签编码器将每个唯一的字符串转换为一个数字，使数据更加灵活，可用于各种算法。对人类来说，结果是一个可怕的数字数组，但对机器来说却很漂亮:

rom sklearn import preprocessing
def encode_features(df_train, df_test):
    features = ['Fare', 'Cabin', 'Age', 'Sex', 'Lname', 'NamePrefix']
    df_combined 以上是关于小白必看的经典机器学习入门项目的主要内容，如果未能解决你的问题，请参考以下文章
 
 前端必看的书籍
 学习React Native必看的几个开源项目
 python 书籍推荐
 新手必看的Springboot入门学习指南
 豆瓣 9 分以上，测试程序员必看的 7 本书
 三分钟教会你Python数据分析—数据导入，小白基础入门必看内容