计算机网络之基本计量单位和进制转换

Posted 2021-07-30 锦衣admin

计算机网络之存储单位

• 计算机及计算机网络中传输、存储、运算基本计量单位
• • 基本计量单位
  • 计算机计量标准
• 进制说明
• • 进制转换
  • 进制转换总结

计算机及计算机网络中传输、存储、运算基本计量单位

基本计量单位

位（bit）：

• 位是计算机内部数据储存的最基本单位。也称比特，可用b来表示
• 数据在物理层就是通过比特流进行传输的
• 计算机中的CPU位数指的是CPU一次能处理的最大位数

字节（byte）：

• 字节是计算机中数据处理的基本单位，计算机中以字节为单位存储和解释信息。可用B表示
• 规定一个字节由八个二进制位构成，即一个字节等于8个比特（1Byte = 8bit）
• 通常1 个字节可以存入一个ASCII码，2个字节可以存放一个汉字国标码。

字（word）：

• 字是计算机进行数据处理时，计算机一次存取、加工和传送的数据长度。一个字通常由一个或多个字节构成
• 例如286微机的字是由两个字节组成，它的字长为16；486微机的字由4个字节组成，它的字节为32位机

字长：

• 字长是计算机中每个字包含的位数。根据计算机的不同，字长有固定和可变两种。固定字长，即长度不论什么情况都是固定不变的；可变字长，则在一定范围内，其长度是可变的
• 计算机的字长是CPU一次操作可以处理的二进制比特数(0或1)。计算机处理数据的速率，自然和它一次能加工的位数以及进行运算的快慢有关

计算机计量标准

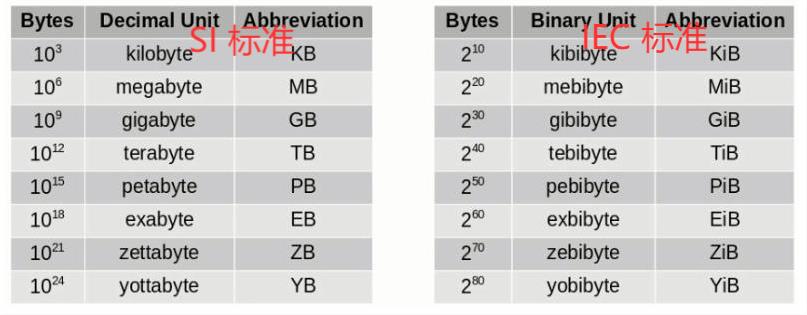
Linux操作系统中两套计量标准：

• SI标准：国际单位制
• IEC标准：国际电工委员会标准

计算机中计量标准：

• 1B = 8b
• 1KB = 1024B
• 1MB = 1024KB
• 1GB = 1024MB
• 1TB = 1024GB
• 1PB = 1024TB
• 1EB = 1024TB

进制说明

进制定义：

进制也就是进位计数制。对于任何一种进制 => x进制，就表示每一个位置上的数运算时都是逢x进一位，如：十进制逢十进1，二进制逢二进1，八进制逢八进1，十六进制逢十六进1

计算机中常用进制：

十进制：

• 逢十进一
• 基符：0，1，2，3，4，5，6，7，8，9
• 比较普遍的一种进制，在工作、学习、生活中随处可见。

二进制：

• 逢二进一
• 基符：0，1
• 多用于计算机中

八进制：

• 逢八进一
• 基符：0，1，2，3，4，5，6，7
• 例如每周循环或Linux系统中权限表示

十六进制：

• 逢十六进一
• 基符：0，1，2，3，4，5，6，7，8，9，A，B，C，D，E，F（a~f）
• 多用于存储大数据中，例如IPV6地址，MAC地址

进制转换

十进制转换为二进制：

	2^7	2^6	2^5	2^4	2^3	2^2	2^1	2^0
	128	64	32	16	8	4	2	1	25510
5						1	0	1
120		1	1	1	1	0	0	0

上图为：十进制5转二进制和十进制120转二进制

(5)₁₀ = (101)₂

(120)₁₀ = (1111000)₂

二进制转换为十进制：

	2^7	2^6	2^5	2^4	2^3	2^2	2^1	2^0
	128	64	32	16	8	4	2	1	25510
(1100)2					1	1	0	0	1210
(10110011)2	1	0	1	1	0	0	1	1	17910

上图为：(1100)₂ = (12)₁₀ 、(10110011)₂ = (179)₁₀

十进制转换为八进制：

	2^7	2^6	2^5	2^4	2^3	2^2	2^1	2^0
	128	64	32	16	8	4	2	1	25510
(120)10		1	1	1	1	0	0	0	(120)8转换为二进制
						0	0	0	从后面三位一组取出08
						1	1	1	从后面三位一组取出78
						0	0	1	从后面三位一组取出18
									最终取出1708

• 由3位二进制可以表示一位八进制，把二进制3位一组转换为八进制。
• 将十进制转换二进制，再转换为八进制

上图为：(120)₂ = (170)₈

八进制转换为十进制：

	2^7	2^6	2^5	2^4	2^3	2^2	2^1	2^0
	128	64	32	16	8	4	2	1	25510
(56)8						1	1	0	取6转换为二进制，三位一组
						1	0	1	取5转换为二进制，三位一组
			1	0	1	1	1	0	完整的二进制
									二进制上的数相加为4610

• 由3位二进制可以表示一位八进制，把二进制3位一组转换为八进制。
• 将八进制转换二进制，在转换十进制

上图为：(56)₈ = (46)₁₀

十进制转十六进制：

	2^7	2^6	2^5	2^4	2^3	2^2	2^1	2^0
	128	64	32	16	8	4	2	1	25510
(120)10		1	1	1	1	0	0	0	转换为二进制
					1	0	0	0	四位一组转换十六进制，816
					0	1	1	1	四位一组转换十六进制，716
									转为十六进制，最终结果为7816

• 由于4位二进制可以表示一位十六进制，把二进制四位一组进行十六进制转换
• 将十进制转化二进制，再转换十六进制

上图为：(120)₁₀ = (78)₁₆

十六进制转换十进制：

	2^7	2^6	2^5	2^4	2^3	2^2	2^1	2^0
	128	64	32	16	8	4	2	1	25510
(A0)16					0	0	0	0	将016转换为二进制
					1	0	1	0	将A16转换为二进制
	1	0	1	0	0	0	0	0	四位一组转换成二进制
									转换为十进制16010转

• 由于4位二进制可以表示一位十六进制，把二进制四位一组进行十六进制转换
• 将十六进制转换为二进制，再转换为二进制

上图为：(A0)₁₆ = (160)₁₀

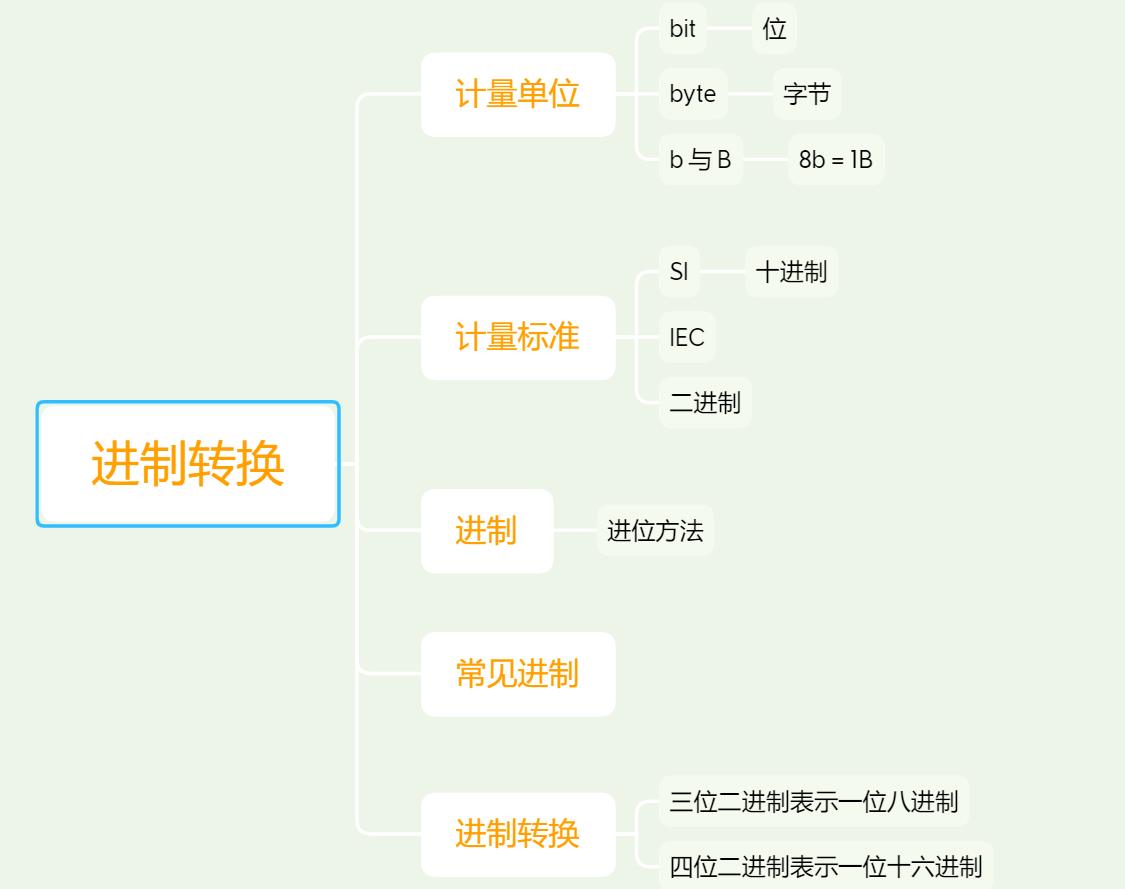
进制转换总结