附Demo时间复杂度到底是如何计算的？

Posted 2021-07-29 chenry777

首先我们要知道，在一个工程中，时间复杂度主要可能存在于2个地方：大循环和网络IO，这是经验，下面让我们分情况来讨论对于各种场景下的时间复杂度，到底是该如何计算的？

首先我们来看张图：

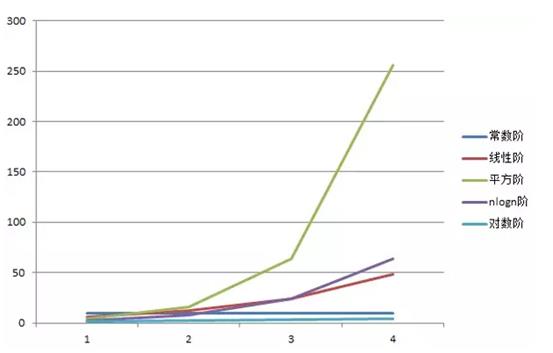
对于常见的时间复杂度，它们的大小关系为：
O(1) < O(log(n)) < O(n) < O(nlog(n)) < O(n²) < O(n^x) (x > 2)

一、O(1)

小技巧：只要循环是确定的，那么这段代码块的时间复杂度就是O(1)

for (int i = 0; i < 3; i++) { // 在第4次的时候结束 跳出 i=3 (0 1 2 3)
    a = a + 1;            //这里会运行3次  O(3) => O(1)
}

二、O(log(n))

小技巧：循环条件不确定，循环体内做乘法或者触发改变循环条件的，时间复杂度就是O(log(n))

二分查找的时间复杂度就是这个哦

while (i <= n) {
    i = i * 3;        //  O(logn)
}

三、O(n)

显而易见，循环会随着n的变化而改变，这种场景的时间复杂度是O(n)

for (i = 0; i < n; i++) {
    a = a + 1;     
}

四、O(nlog(n))

在复杂度为log(n)的循环外层再套一层循环，时间复杂度就是O(nlog(n))

for (int j = 0; j < n; j++) {
    while (i <= n) {
        i = i * 2;
    }
}

五、O(n²)

小技巧：注意有个规律，有加减法的时候，找次数最高的那个

冒泡排序的时间复杂度就是这个哦

for (i = 0; i < n; i++) {    // 乘法 n次
    for (int j = 0; j < n; j++) {        //n次
        a = a + 1;            //运行了n^2次     时间复杂度：O(n^2)
    }
}

for (i = 0; i < n; i++) {    // 乘法 n次
    for (int j = i; j < n; j++) {        //n次
        a = a + 1;            //运行了多少次？	n*(n+1)/2 => O(n^2); => (n^2+n)/2 

    }
}

除了以上的5种常见情况外，在工程开发中，往往会有着大量的网络IO交互，比如RPC远程服务调用、HTTP接口访问、访问数据库等，这些都有可能是造成接口访问时间过长的瓶颈所在。那么平时该如何检测这些地方的时间损耗呢？

有一种常用的办法：

我们可以在网络IO的前后计算当前的时间戳：System.currentTimeMillis()
在外层套一个循环多统计几次，对统计的前后时间戳之差求和后，求平均

这样就能大概定位到"慢执行"的位置了

你学会了吗？ O(∩_∩)O