数据结构——二叉树根节点到特定节点路径(C语言版)
Posted 行稳方能走远
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构——二叉树根节点到特定节点路径(C语言版)相关的知识,希望对你有一定的参考价值。
摘自:数据结构——二叉树根节点到特定节点路径(C语言版)
作者:正弦定理
发布时间:2020-12-10 21:09:43
网址:https://blog.csdn.net/chinesekobe/article/details/110991771
#include<stdio.h>
#include<stdlib.h>
// 二叉树结构体
typedef struct TreeLink{
int Data;
struct TreeLink *LChild; // 左子树指针
struct TreeLink *RChild; // 右子树指针
}T_LINK,*TLINK;
// 链栈
typedef struct STACK{
int data;
struct STACK *next;
}StackNode,*Stack;
int flag; // 标记符
Stack L; // 链栈头节点指针
//************************* 二叉树 ***********************//
// 创建二叉树
TLINK Create_TreeLink()
{
TLINK T;
int data;
int temp;
scanf("%d",&data);
temp = getchar(); // 吸收scanf带来的回车
if(data == -1){ // 输入-1表示该节点下左树或者右树下不存数据,返回到上一级节点
return NULL;
}else{
T = (TLINK)malloc(sizeof(T_LINK)); // 每个节点开辟空间
T->Data = data;
printf("请输入%d节点下左节点数据: ",data);
T->LChild = Create_TreeLink();
printf("请输入%d节点下右节点数据: ",data);
T->RChild = Create_TreeLink();
return T;
}
}
// 先序遍历二叉树
void ShowXianXu(TLINK S)
{
if(S==NULL){
return;
}
printf("%d ",S->Data);
ShowXianXu(S->LChild);
ShowXianXu(S->RChild);
}
//************************* 链 栈 *********************//
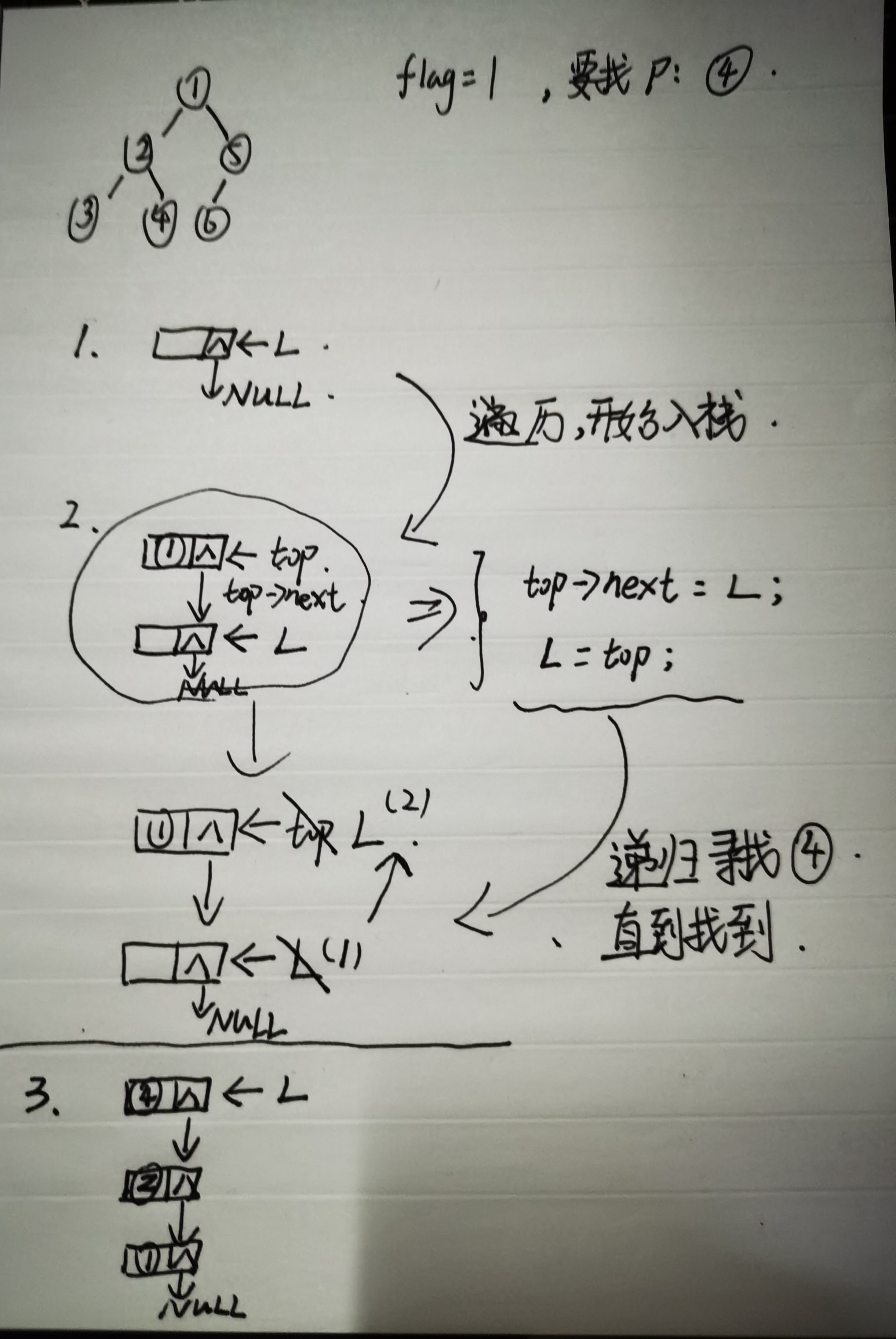
// 入栈
void PushStack(int x)
{
Stack top;
top = (Stack)malloc(sizeof(StackNode));
top->data = x;
top->next = L; // 第一次是让一开始的头节点存入元素,尾巴指向NULL已经初始化好
L = top; // 之后便是创建新的链栈节点和之前的串起来
}
// 出栈
int PopStack()
{
int x;
if(L->next==NULL) // 栈空
{
printf("出栈完毕\\n");
exit(-1);
}else{
Stack p;
x = L->data;
p = L; // 让原来的L变成P
L = p->next; // 原来头节点next指向的变成新的头节点
free(p); // 释放原来的头节点
return x; // 返回原来头节点里头的元素
}
}
// 进入二叉树搜索特定节点
void CherkNode(TLINK T,int data)
{
if(T==NULL)
{
return;
}
if(flag==1) // 标记符flag 还是1时,表示还没找到要找的节点
{
printf("入栈元素为: %d\\n",T->Data);
PushStack(T->Data); // 入栈
}
if(T->Data == data) // 已经在二叉树中遍历到要找的节点元素
{
printf("元素找到,元素为: %d\\n",T->Data);
flag = 0;
return;
}
CherkNode(T->LChild,data); // 遍历这个节点左子树,为NULL时才结束递归,返回上一级节点
CherkNode(T->RChild,data); // 遍历这个节点的右子树,为NULL时返回上一级节点
if(flag==1) // 递归遍历二叉树每条路径中寻找,由于遍历一个节点
{ // 就会让元素入栈,以便将后面元素不是要找路径之中的元素,从栈中清除
printf("出栈元素: %d\\n",T->Data);
PopStack(); // 清除非要寻找路径上的栈中元素
}
}
// 搜索路径
void SearchPath(TLINK T,int data)
{
int temp[30]; // 用来存最后找到的路径各个节点里头的数据
int i;
flag = 1; // 标记符
L = (Stack)malloc(sizeof(StackNode)); // 分配空间给指针
L->next = NULL; // 让第一个节点指针指向NULL,最后也就是栈底指针
if(T==NULL) // 空树
{
return;
}
CherkNode(T,data); // 搜索二叉树中要找的节点,进行入栈出栈操作
for(i=0;L->next;i++)
{
temp[i] = PopStack(); // 找到的路径元素逆序存放在数组temp[]中
}
printf("路径寻找成功,路径如下:\\n");
for(i--;i>=0;i--)
{
printf("%d ",temp[i]);
}
}
// 主函数
int main()
{
TLINK T; // 创建二叉树指针
int Node;
printf("请输入第一个节点(输入-1表示该节点下无其他节点)\\n");
T = Create_TreeLink();
printf("先序遍历如下:\\n");
ShowXianXu(T);
putchar('\\n');
printf("请输入你要找的特定节点:\\n");
scanf("%d",&Node);
SearchPath(T,Node); // 开始搜索节点
return 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
运行结果:
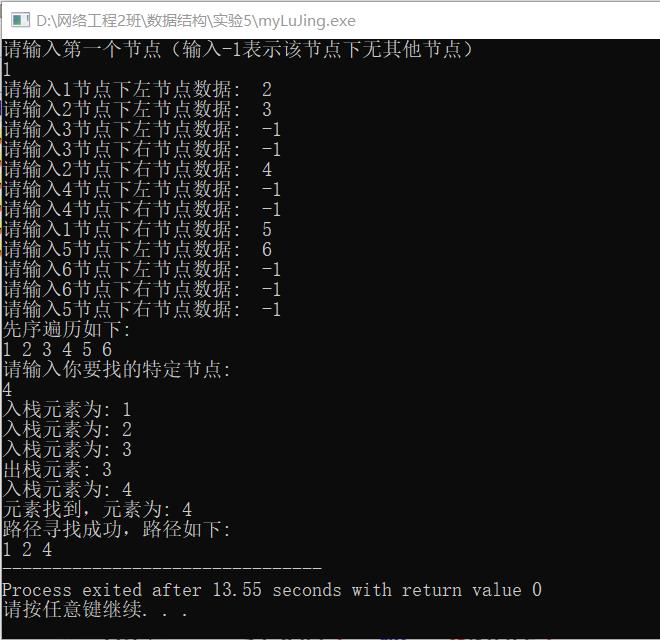
以上是关于数据结构——二叉树根节点到特定节点路径(C语言版)的主要内容,如果未能解决你的问题,请参考以下文章
二叉树根节点到叶子节点和为指定值的路径(NC8/考察次数Top54/难度中等)
[javascript]二叉树根节点到叶子节点和为指定值的路径