[Hbfs] lc815. 公交路线(建图+多源bfs+bfs最短路+思维+好题)

Posted 2021-07-28 Ypuyu

文章目录

• • 1. 题目来源
  • 2. 题目解析

1. 题目来源

链接：815. 公交路线

相似：[最短路] aw920. 最优乘车(单源最短路建图+bfs最短路模型+知识理解+好题)

2. 题目解析

好题，之前做过，但似懂非懂。

---

问题抽象：

每一个公交线路都是一个环，如果两环有公共点，则这两个环相连。

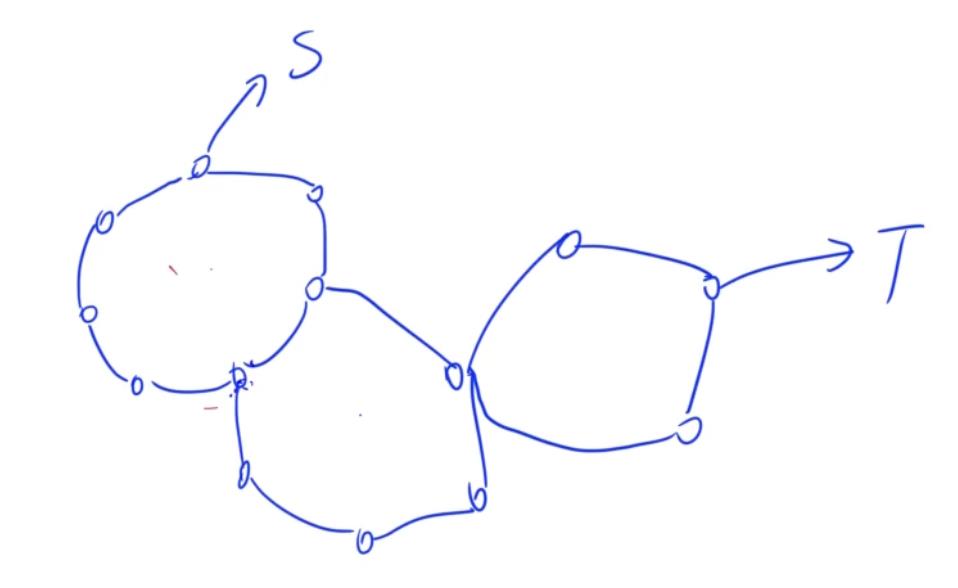
本题是求最少经过几个公交车，从起点 S 到达终点 T，即等价于从起点经过最少的环到达终点。

则可以将每个环看成一个点，其公共点就代表两点之间有边相连。在此依据题意，边为无向边。

故，在此边权为 1，求起点到终点的最短距离，那么就是 bfs 最短路模型了。

---

建图：

• 如何建立点边之间的关系是本题建图一大难点，方法也有很多，在此具体实现如下：
  • 将环抽象成点。
  • 环相连，等价于两环中存在公共点，则一个公共点提供一条边。
  • 由于起点可能是多个环的公共点，且从任意一个环出发都是合理的，所以本题是多源 bfs 问题，需要将起点所在环全部入队。
  • bfs 一开始存的为起点所在的环编号，然后遍历起点所在环内的所有点，其中这些点有可能通向其它的环，如果其它的环还未被拓展到的话，那么说明从该环到另一个环的最短路就被找到了。
  • bfs 最短路，第一次遍历到的一定是最短的。可以拿距离判断，也可以拿非法值来判断。即针对 dist 数组有两种初始化方式，dist[i]=-1 或 dist[i]=1e9，前者在更新时仅需判断 dist[y]==-1 即可判断环 y 是否是第一次更新，后者需要判断距离，即 dist[y]>dist[x]+1 这个也是象征性的判断，因为不存在多次更新的情况，bfs 第一次遍历第一次更新一定是最小的。
  • 在遍历每个环中的各个点时，顺便判断终点。

---

时间复杂度：$O(n+m)$，每个点只会被遍历一次

空间复杂度：$O(n)$

---

class Solution {
public:
    int numBusesToDestination(vector<vector<int>>& routes, int source, int target) {
        if (source == target) return 0;         // 起点终点相同
        int n = routes.size();
        unordered_map<int, vector<int>> g;
        vector<int> dist(n, 1e9);
        queue<int> q;

        // 建图
        for (int i = 0; i < n; i ++ ) {
            for (auto x : routes[i]) {
                if (x == source) {              // 多源，初始化、入队
                    dist[i] = 1;
                    q.push(i);                  // 若起点在多个环上，则这些环都能当做起点使用，故是多源问题
                }
                g[x].push_back(i);              // 每个点所在的环形公交路线
            }
        }

        // bfs
        while (q.size()) {
            auto t = q.front(); q.pop();

            for (auto x : routes[t]) {
                if (x == target) return dist[t];
                for (auto y : g[x]) {
                    if (dist[y] > dist[t] + 1) {
                        dist[y] = dist[t] + 1;
                        q.push(y);
                    }
                }
                g.erase(x);
            }
        }

        return -1;
    }
};