数据结构《四》二叉树的实现

Posted AURORA_CODE

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数据结构《四》二叉树的实现相关的知识，希望对你有一定的参考价值。

队列

1.树的概念

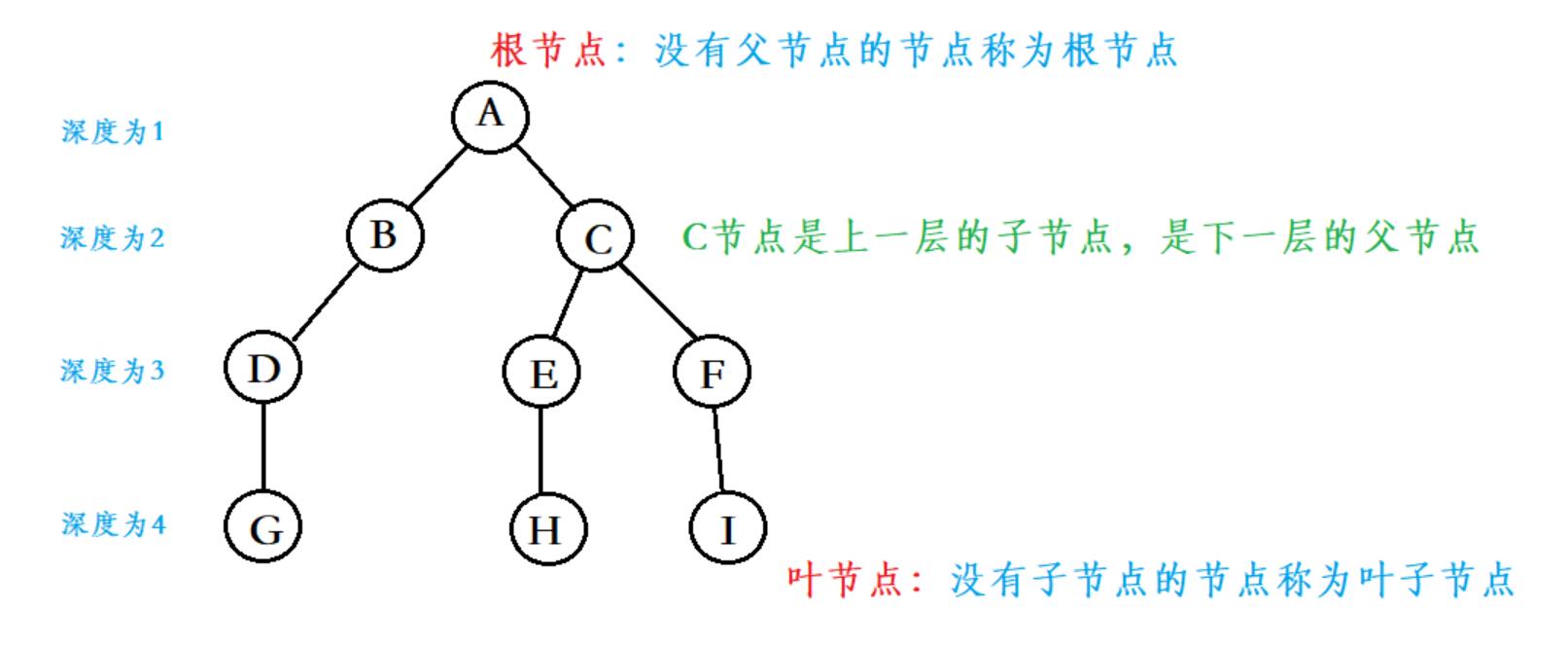
树是一种非线性的数据结构，它是由n（n>=0）个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。
在这里插入图片描述

  • 根结点：根节点没有前驱结点。除根节点外，其余结点被分成是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱，可以有0个或多个后继。因此，树是递归定义的。

  • 节点的度：一个节点含有的子树的个数称为该节点的度； 如上图：A的为2

  • 叶节点：度为0的节点称为叶节点； 如上图：G、H、I节点为叶节点

  • 非终端节点或分支节点：度不为0的节点； 如上图：B、D、C、E、F节点为分支节点

  • 双亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点； 如上图：A是B的父节点

  • 孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点； 如上图：B是A的孩子节点

  • 兄弟节点：具有相同父节点的节点互称为兄弟节点； 如上图：B、C是兄弟节点

  • 树的度：一棵树中，最大的节点的度称为树的度； 如上图：树的度为2

  • 节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推；

  • 树的高度或深度：树中节点的最大层次； 如上图：树的高度为4

  • 堂兄弟节点：双亲在同一层的节点互为堂兄弟；如上图：H、I互为兄弟节点

  • 节点的祖先：从根到该节点所经分支上的所有节点；如上图：A是所有节点的祖先

  • 子孙：以某节点为根的子树中任一节点都称为该节点的子孙。如上图：所有节点都是A的子孙

  • 森林：由m棵互不相交的树的集合称为森林；

2. 二叉树的概念

一棵二叉树是结点的一个有限集合，该集合或者为空，或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成。
二叉树的特点：

  1. 每个结点最多有两棵子树，即二叉树不存在度大于2的结点。
  2. 二叉树的子树有左右之分，其子树的次序不能颠倒。

特殊二叉树：

  1. 满二叉树

一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是说，如果一个二叉树的层数为K，且结点总数是(2^k) -1 ，则它就是满二叉树。

  1. 完全二叉树

完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树。当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。

3. 二叉树的性质

  • 若规定根节点的层数为1，则一棵非空二叉树的第i层上最多有2^(i-1) 个结点.
  • 若规定根节点的层数为1，则深度为h的二叉树的最大结点数是2^h- 1.
  • 对任何一棵二叉树, 如果度为0其叶结点个数为 n0, 度为2的分支结点个数为 n2,则有n0＝n2＋1
  • 若规定根节点的层数为1，具有n个结点的满二叉树的深度，h=Log2(n+1). (ps：Log2(n+1)是log以2为底，n+1为对数)
  • 对于具有n个结点的完全二叉树，如果按照从上至下从左至右的数组顺序对所有节点从0开始编号，则对于序号为i的结点有：
  1. 若i>0，i位置节点的双亲序号：(i-1)/2；i=0，i为根节点编号，无双亲节点
  2. 若2i+1<n，左孩子序号：2i+1，2i+1>=n否则无左孩子
  3. 若2i+2<n，右孩子序号：2i+2，2i+2>=n否则无右孩子

4. 二叉树的功能实现

01 创建二叉树与销毁二叉树

typedef int BDataType;
typedef struct BTNode
{
	BDataType data;
	struct BTNode *left;
	struct BTNode *right;
}BTNode;
BTNode* BuyBinartTreeNode(BDataType data)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	if (NULL == node)
	{
		assert(0);
		return NULL;
	}
	node->data = data;
	node->left = NULL;
	node->right = NULL;
	return node;
}

// 创建二叉树
BTNode* X_CrteateBinTree(BDataType array[], int size,int* index, BDataType invalid)
{
	BTNode* root = NULL;
	if (*index < size && invalid != array[*index])
	{
		//创建根结点
		root = BuyBinartTreeNode(array[*index]);
		++(*index);
		//创建左子树
		root->left = X_CrteateBinTree(array, size, index, invalid);
		++(*index);
		//创建右子树
		root->right = X_CrteateBinTree(array, size, index, invalid);
	}
	return root;
}
BTNode* CrteateBinTree(BDataType array[], int size, BDataType invalid)
{
	int index = 0;
	return X_CrteateBinTree(array, size, &index, invalid);
}
// 销毁二叉树
void DestroyBinTree(BTNode** root)
{
	if (NULL == *root)
		return;
	//按照后序遍历的方法进行销毁
	DestroyBinTree(&(*root)->left);
	DestroyBinTree(&(*root)->right);
	free(*root);
	*root = NULL;

}

02 二叉树的遍历

a） 二叉树的前序遍历

void PreOrder(BTNode* root)
{
	if (NULL != root)
	{ 
		// 先输出根结点的值
		// 然后遍历左子树
		// 最后遍历右子树
		printf("%d", root->data);
		PreOrder(root->left);
		PreOrder(root->right);
	}
}

b）二叉树的中序遍历

void InOrder(BTNode* root)
{
	if (NULL != root)
	{
		// 先遍历左子树
		// 然后输出根结点的值
		// 最后遍历右子树
		InOrder(root->left);
		printf("%d", root->data);
		InOrder(root->right);
	}
}

c）二叉树的后序遍历

void PostOrder(BTNode* root)
{
	if (NULL != root)
	{
		// 先遍历左子树
		// 然后遍历右子树
		// 最后输出根结点的值
		PreOrder(root->left);
		PreOrder(root->right);
		printf("%d", root->data);
	}
}

d) 二叉树的层序遍历

void LevelOrder(BTNode* root)
{
	//先创建一个队列，并初始化队列
	//将队列的根结点压入队列。
	//设置循环，将队头结点输出同时将该结点的左右子树压入队列（如果存在），最后将队头结点出队；
	Queue q;
	if (NULL == root)
		return;
	QueueInit(&q);
	QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		BTNode* cur = QueueFront(&q);
		printf("%d", cur->data);
		if (cur->left)
		{
			QueuePush(&q, cur->left);
		}
		if (cur->right)
		{
			QueuePush(&q, cur->right);
		}
		QueuePop(&q);
	}
	QueueDestroy(&q);
}

03 求二叉树中结点个数

int BinaryTreeSize(BTNode* root)
{
	return NULL == root ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}

04 求二叉树叶子结点个数

int BinaryTreeLeafSize(BTNode* root)
{
	if (NULL == root)
		return 0;
	if (NULL == root->left&&NULL == root->right)
		return 1;
	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

05 求二叉树第k层结点个数

int BinaryTreeLevelKSize(BTNode* root, int k)
{
	if (NULL == root || k == 0)
		return 0;
	if (1 == k)
		return 1;
	return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}

06 求二叉树的高度

int BinaryTreeHeight(BTNode* root)
{
	if (root)
	{
		int leftheight = BinaryTreeHeight(root->left);
		int rightheight = BinaryTreeHeight(root->right);
		return leftheight > rightheight ? leftheight : rightheight;
	}
	return 0;
}

07 二叉树查找值为x的结点

BTNode* BinaryTreeFind(BTNode* root, BDataType x)
{
	BTNode* retnode;
	if (NULL == root)
		return NULL;
	//
	if (x == root->data)
		return root;
	if (retnode = BinaryTreeFind(root->left, x))
		return retnode;
	return BinaryTreeFind(root->right, x);
}

08 判断二叉树是否为完全二叉树

int BinaryTreeComplete(BTNode* root)
{
	//用层序遍历的方式进行判断
	Queue q;
	int flag = 0;
	// 当二叉树为空树的时候他是完全二叉树
	if (NULL == root)
		return 1;
	QueueInit(&q);
	QueuePush(&q, root);
	while (QueueEmpty(&q))
	{
		BTNode* cur = QueueFront(&q);
		if (flag)// 从第一个不包含节点之后，所有的节点不能有孩子
		{
			if (cur->left || cur->right)
			{
				QueueDestroy(&q);
				return 0;
			}
		}
		else
		{
			if (cur->left && cur->right)
			{
				QueuePush(&q, cur->left);
				QueuePush(&q, cur->right);
			}
			else if (cur->left)//如果左不为空，右为空，更改标记
			{
				QueuePush(&q, cur->left);
				flag = 1;
			}
			else if (cur->right)//如果右不为空，左为空，则一定不是完全二叉树
			{
				QueueDestroy(&q);
				return 0;
			}
			else//如果左右都为空，则更改标记为1
			{
				flag = 1;
			}
		}
		QueuePop(&q);
	}
	QueueDestroy(&q);
	return 1;
}

以上是关于数据结构《四》二叉树的实现的主要内容，如果未能解决你的问题，请参考以下文章

二叉树，堆详解

数据结构C语言 《四》二叉树，堆的基本概念以及堆的相关操作实现（上）

数据结构C语言 《四》二叉树，堆的基本概念以及堆的相关操作实现（上）

数据结构学习笔记——广义表树和二叉树的基本知识

二叉树需要掌握的基本知识

数据结构C语言 《四》二叉树链式的实现及操作《下》