C++____二叉搜索树

Posted 2021-07-25 Y—X

1. 二叉搜索树概念

二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:

• 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
• 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
• 它的左右子树也分别为二叉搜索树
  
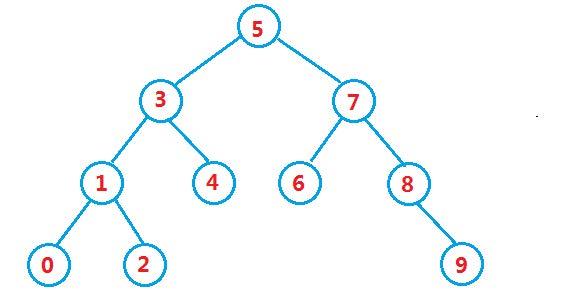
  int a [] = {5,3,4,1,7,8,2,6,0,9};

template <class K>
struct BSTreeNode
{
	K _key;
	BSTreeNode<K>* _left;
	BSTreeNode<K>* _right;

	BSTreeNode(const K& key)
		:_key(key)
		, _left(nullptr)
		, _right(nullptr)
	{}
};

2. 二叉搜索树操作

1. 二叉搜索树的查找

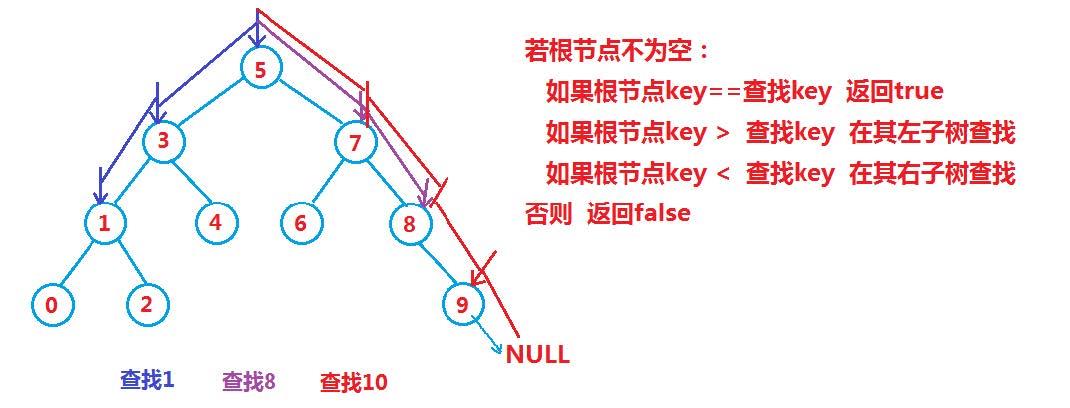
const Node* Find(const K& key)
	{
		Node* cur = _root;
		while (cur != nullptr)
		{
			if (cur-> _key > key)
			{
				cur = cur->_left;
			}
			else if (cur->_key < key)
			{
				cur = cur->_right;
			}
			else
			{
				return cur;
			}
		}
		return cur;
	}

2. 二叉搜索树的插入

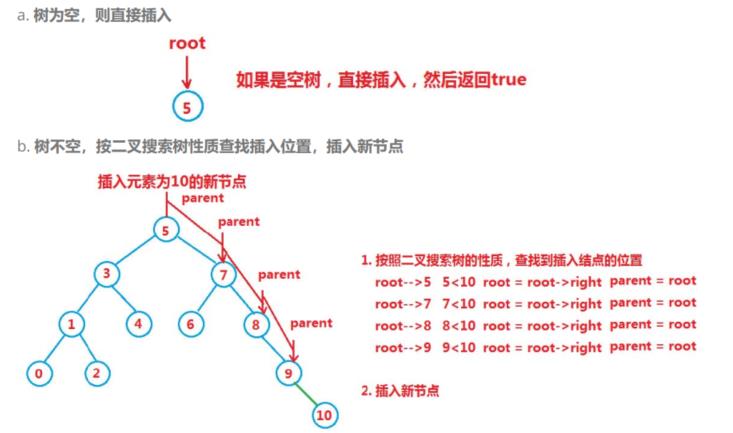
bool Insert(const K& key)
	{
		if (_root == nullptr)
		{
			_root = new Node(key);
			return true;
		}

		Node* parent = nullptr;
		Node* cur = _root;
		while (cur != nullptr)
		{
			if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				return false;
			}
		}

		Node* newNode = new Node(key);
		if (parent->_key > key)
		{
			parent->_left = newNode;
		}
		else
		{
			parent->_right = newNode;
		}
		return true;
	}

3. 二叉搜索树的删除
首先查找元素是否在二叉搜索树中，如果不存在，则返回, 否则要删除的结点可能分下面四种情况：

1. 要删除的结点无孩子结点
2. 要删除的结点只有左孩子结点
3. 要删除的结点只有右孩子结点
4. 要删除的结点有左、右孩子结点

bool Erase(const K& key)//替代法
	{
		Node* parent = nullptr;
		Node* cur = _root;
		//1.叶子 2.单孩子 3.俩个孩子
		while (cur)
		{
			if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				//删除
				//1.左为空 2.右为空 3.左右都不为空
				if (cur->_left == nullptr)
				{
					if (cur == _root)//cur为根节点
					{
						_root = cur->_right;
					}
					else
					{
						if (cur == parent->_left)
						{
							parent->_left = cur->_right;
						}
						else
						{
							parent->_right = cur->_right;
						}
					}

					delete cur;//删除
				}
				else if (cur->_right == nullptr)//2.右为空
				{
					if (cur == _root)
					{
						_root = cur->_left;
					}
					else
					{
						if (cur == parent->_left)
						{
							parent->_left = cur->_left;
						}
						else
						{
							parent->_right = cur->_left;
						}
					}

					delete cur;//删除
				}
				else//左右都不为空
				{
					//替代法删除，右树最小节点
					Node* smParent = cur;//右子树的根可能是最小节点
					Node* subMin = cur->_right;
					while (subMin->_left)
					{
						smParent = subMin;
						subMin = subMin->_left;
					}
					cur->_key = subMin->_key;//赋给删除节点
					if (smParent->_left ==  subMin)
					{
						smParent->_left = subMin->_right;
					}
					else
					{
						smParent->_right = subMin->_right;
					}

					delete subMin;
				}
				return true;
			}
		}
		return false;
	}

完整代码：

#pragma once
#include <iostream>
using namespace std;

template <class K>
struct BSTreeNode
{
	K _key;
	BSTreeNode<K>* _left;
	BSTreeNode<K>* _right;

	BSTreeNode(const K& key)
		:_key(key)
		, _left(nullptr)
		, _right(nullptr)
	{}
};

template <class K>
class BSTree
{
	typedef BSTreeNode<K> Node;
public:
	bool Insert(const K& key)
	{
		if (_root == nullptr)
		{
			_root = new Node(key);
			return true;
		}

		Node* parent = nullptr;
		Node* cur = _root;
		while (cur != nullptr)
		{
			if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				return false;
			}
		}

		Node* newNode = new Node(key);
		if (parent->_key > key)
		{
			parent->_left = newNode;
		}
		else
		{
			parent->_right = newNode;
		}
		return true;
	}

	bool Erase(const K& key)//替代法
	{
		Node* parent = nullptr;
		Node* cur = _root;
		//1.叶子 2.单孩子 3.俩个孩子
		while (cur)
		{
			if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				//删除
				//1.左为空 2.右为空 3.左右都不为空
				if (cur->_left == nullptr)
				{
					if (cur == _root)//cur为根节点
					{
						_root = cur->_right;
					}
					else
					{
						if (cur == parent->_left)
						{
							parent->_left = cur->_right;
						}
						else
						{
							parent->_right = cur->_right;
						}
					}

					delete cur;//删除
				}
				else if (cur->_right == nullptr)//2.右为空
				{
					if (cur == _root)
					{
						_root = cur->_left;
					}
					else
					{
						if (cur == parent->_left)
						{
							parent->_left = cur->_left;
						}
						else
						{
							parent->_right = cur->_left;
						}
					}

					delete cur;//删除
				}
				else//左右都不为空
				{
					//替代法删除，右树最小节点
					Node* smParent = cur;//右子树的根可能是最小节点
					Node* subMin = cur->_right;
					while (subMin->_left)
					{
						smParent = subMin;
						subMin = subMin->_left;
					}
					cur->_key = subMin->_key;//赋给删除节点
					if (smParent->_left ==  subMin)
					{
						smParent->_left = subMin->_right;
					}
					else
					{
						smParent->_right = subMin->_right;
					}

					delete subMin;
				}
				return true;
			}
		}
		return false;
	}

	const Node* Find(const K& key)
	{
		Node* cur = _root;
		while (cur != nullptr)
		{
			if (cur-> _key > key)
			{
				cur = cur->_left;
			}
			else if (cur->_key < key)
			{
				cur = cur->_right;
			}
			else
			{
				return cur;
			}
		}
		return cur;
	}

	void _InOrder(Node* root)
	{
		if (root == nullptr)
		{
			return;
		}

		_InOrder(root->_left);
		std::cout << root->_key << " ";
		_InOrder(root->_right);
	}

	void InOrder()
	{
		_InOrder(_root);
		cout << endl;
	}

private:
	Node* _root = nullptr;
};