力扣1两数之和（简单）

Posted 2021-07-25 小布丁value

两数之和

• 方法一：暴力枚举
• 方法二：哈希表

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target 的那 两个
整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。

方法一：暴力枚举

将所有可能的出现的情况相加 时间复杂度：O(N^2) 其中 N是数组中的元素数量。最坏情况下数组中任意两个数都要被匹配一次。
空间复杂度：O(1)

public static int [] twoSum(int [] nums,int target) throws IllegalAccessException {
       int len = nums.length;
       for(int i=0;i<len -1;i++){
           for(int j=i+1;j<len;j++){
               if(nums[i]+nums[j] == target){
                   return new int[]{i,j};
               }
           }
       }
     throw new IllegalAccessException("No two sum solution");

   }

示例

输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] ==9
返回 [0, 1] 。

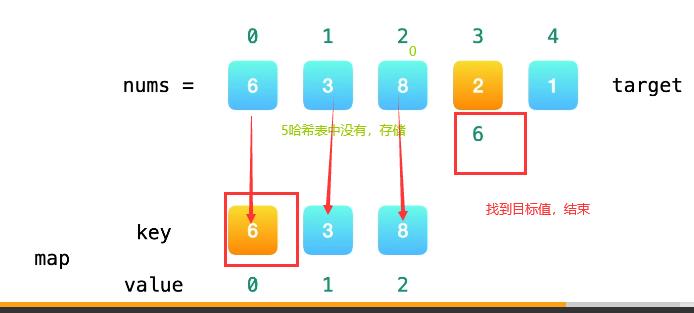
方法二：哈希表

思路及算法 注意到方法一的时间复杂度较高的原因是寻找 target - x
的时间复杂度过高。因此，我们需要一种更优秀的方法，能够快速寻找数组中是否存在目标元素。如果存在，我们需要找出它的索引。
使用哈希表，可以将寻找 target - x 的时间复杂度降低到从 O(N)O(N) 降低到 O(1)O(1)。
这样我们创建一个哈希表，对于每一个 x，我们首先查询哈希表中是否存在 target - x，然后将 x 插入到哈希表中，即可保证不会让 x
和自己匹配。

时间复杂度：O(N)其中 NN是数组中的元素数量。对于每一个元素 x，我们可以 O(1)地寻找 target - x。
空间复杂度：O(N)其中 N 是数组中的元素数量。主要为哈希表的开销。

  public static void main(String[] args) {
        int [] nums = {3,2,4};
        int target = 6;
        int[] a = twoSun(nums, target);
        System.out.println(Arrays.toString(a));  
    }
    public static int [] twoSun(int [] nums, int target){
        int len = nums.length;
       Map<Integer,Integer> map= new HashMap<>(len-1);
        for(int i=0;i<len;i++){
            if(map.containsKey(target-nums[i])){
                return new int[]{map.get(target - nums[i]),i};
            }
            map.put(nums[i],i);
        }
        return new int[0];
    }
}

测试结果：