运筹学-图论实例

Posted 2021-07-25 书槑

图论中一些简单的计算，并用R语言实现。

目录

• 最短路问题
• • Dijkstra算法
  • R语言实现
• 最大流与最小割
• • 割集的定义
  • 割集的容量
  • 最大流-最小割问题
  • R语言实现

最短路问题

求连通图任意两点间总权最小的路

Dijkstra算法

对每一个顶点给出一组标号，其中第一位代表从始点到该点最短路权的上界，第二位代表该点的上一个点，第三位是T或P，T表示试探性标号，是一种临时标 号，P表示永久性标号，即这个标号不会改变。标有P的点，其第一位标号即为最短路权。算法的每一步都把某一点的T标号改为P标号，当终点被标上P时，全部计算结束。

以这个图为例，我们要求O到T的最短路：

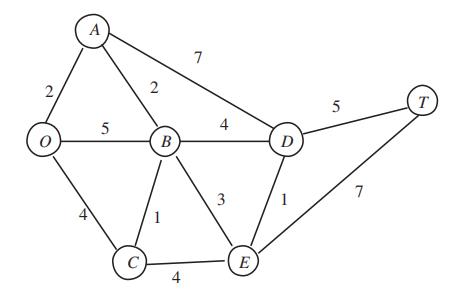
第一步：
（注意，从O无法一步到达的点，路权标为∞，此时只有A，B，C有路权）

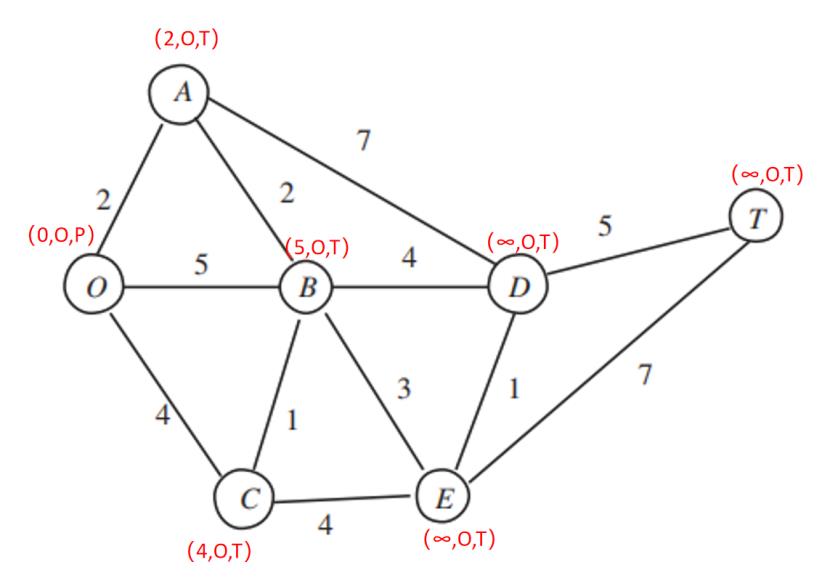
第二步：
比较A，B，C的路权大小，取最小的点A，将T改为P
从A点出发，修改相邻的B，D点的路权

第三步：
发现B的路权小于D，因此将B改为P标号
从B点出发，修改相邻的D，E点的路权
因为从B出发到C的路权为4+1=5，小于从O直接到C的路权，因此C点路权不变，但也改为P标号

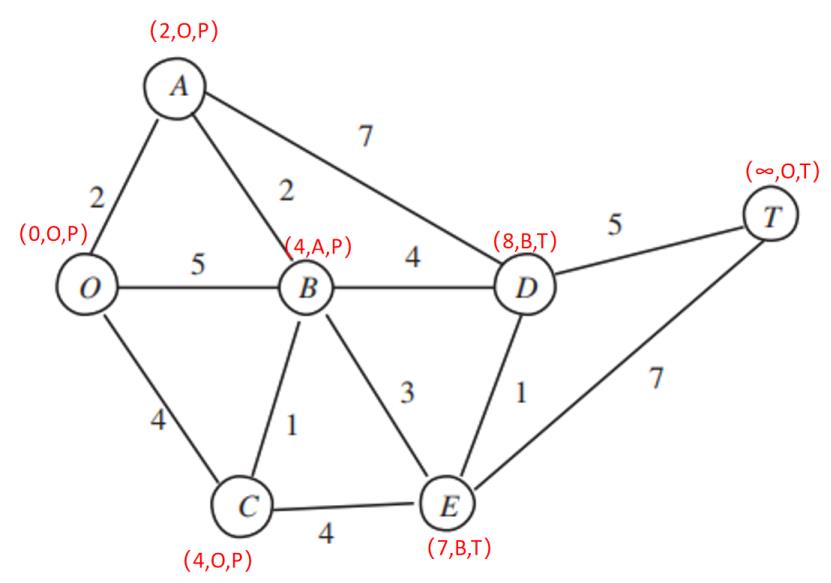
第四步：
发现E的路权小于D，因此将E改为P标号
从E点出发，修改相邻的D，T点的路权
D点路权不变（所以第二位不用改），且小于T，改为P标号

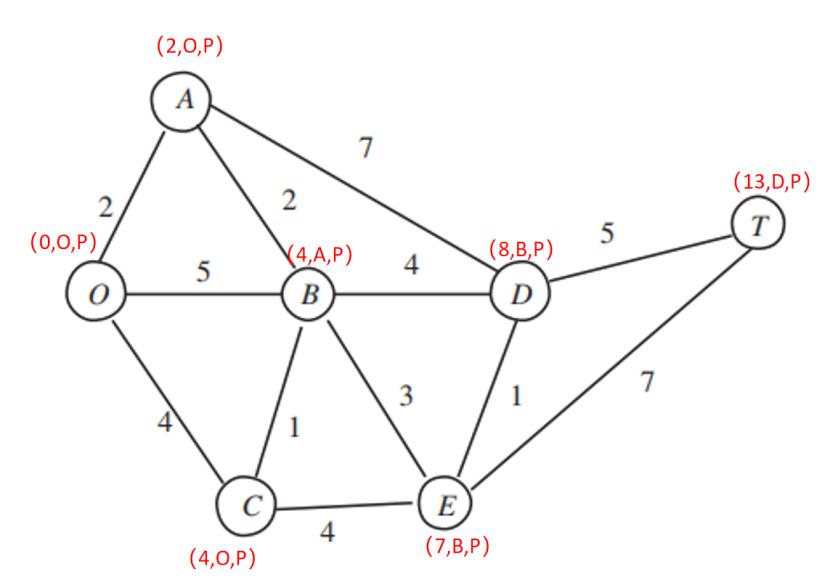
第五步：
从D出发，修改相邻T点的路权
T点改为P标号
算法结束

R语言实现

为了将图用编程语言展现，我们需要将图存为邻接矩阵

邻接矩阵中的$a_{ij}$表示$v_i$到$v_j$的路权，若不能一步到达则记为0，若是自己到自己也记为0

将点O,A,B,C,D,E,T分别记为1，2，3，4，5，6，7

library('igraph')
library('magrittr')
a1 = c(0,2,5,4,rep(0,3))  
a2 = c(2,0,2,0,7,0,0)
a3 = c(5,2,0,1,4,3,0)
a4 = c(4,0,1,0,0,4,0)
a5 = c(0,7,4,0,0,1,5)
a6 = c(0,0,3,4,1,0,7)
a7 = c(0,0,0,0,5,7,0)
a = rbind(a1,a2,a3,a4,a5,a6,a7)
g = graph.adjacency(a, mode = c('undirected'), weighted = TRUE)  #生成图,无向，数字为权重,否则当作多重边处理
shortest.paths(g,1,7)   #1到7的最短路

算出的答案为13，即O到T的最短路

还可以顺便看一下最小生成树。
树是指连通且不含圈的无向图，若图的生成子图是一棵树，则称为该图的生成树，其中具有最小权的生成树称为最小生成树。

minimum.spanning.tree(g)  #有权重
minimum.spanning.tree(g, algorithm = 'unweighted')  #无权重

最大流与最小割

最大流问题是指在交通运输网络中使运输量最大化，图上的数字代表运输量限制，例如下图

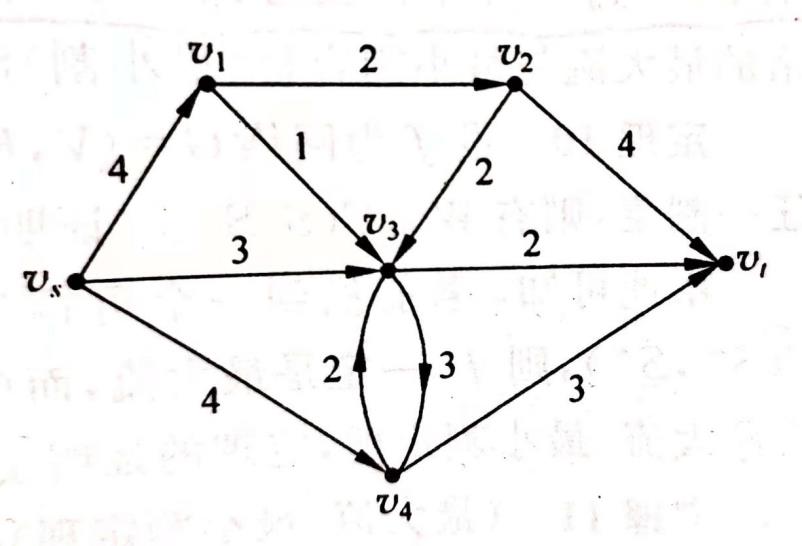
割集的定义

容量网络G=(V,E,C),$v_s,v_t$为发、收点，若有边集E‘为E的子集，满足：G(V,E-E’)不连通；E’’为E的真子集，而G(V,E-E’’)仍联通，则称E’为G的割集，记为E’=$(S,S\overline{)}$.
即：将容量网络分为互补的两部分，分别包含发、收点，连通这两部分的边称为割集。

割集的容量

割集$(S,S\overline{)}$中所有始点在$S$，终点在$\overline{S}$的边的容量之和

例如，边集$(v_s,v_1),(v_1,v_3),(v_2,v_3),(v_3,v_t),(v_4,v_t)$是G的割集，按这些边画一条线，将图分成$S$和$\overline{S}$，则边集中所有从$S$指向$\overline{S}$的边上的容量才被算作割集的容量（图中已标黄），因此这个割集的容量是9.

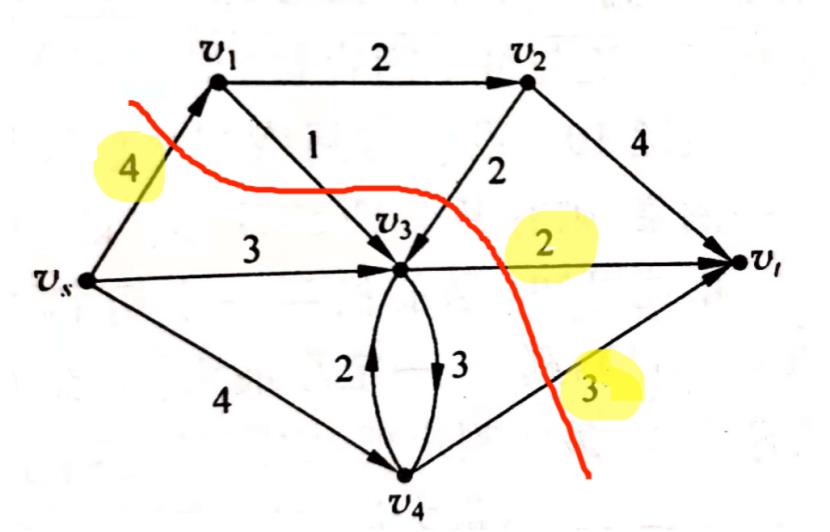
最大流-最小割问题

在容量网络中割集是由$v_s$到$v_t$的必经之路，所以任何一个可行流的流量都不会超过任一割集的容量。因此若能找到一个可行流的流量等于某一割集的容量，则该可行流为最大流，相应的割集为最小割。

以这幅图为例，每条边上的前一个数字表示流量限制，后一个数字表示初始可行流。

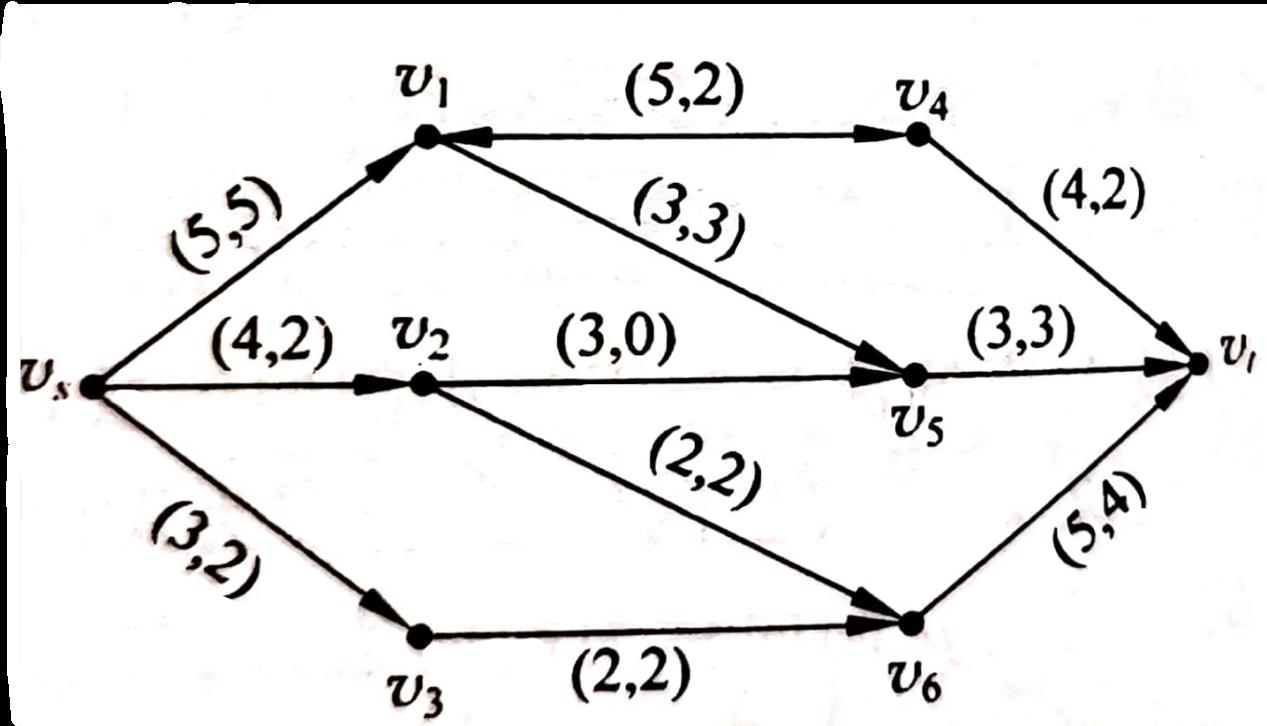
R语言实现

从$v_s$开始输入，同理，自己到自己标为0，无法到达标为0，逆流（如$v_1$到$v_s$）也标为0.

library('igraph')
#输入的数字为流量限制
r1 = c(0,5,4,3,rep(0,4))    
r2 = c(rep(0,4),5,3,0,0)
r3 = c(rep(0,5),3,2,0)
r4 = c(rep(0,6),2,0)
r5 = c(0,5,rep(0,5),4)
r6 = c(rep(0,7),3)
r7 = c(rep(0,7),5)
r8 = rep(0,8)
adj = rbind(r1,r2,r3,r4,r5,r6,r7,r8)
g = graph.adjacency(adj, mode = c('directed'), weighted = TRUE) 
vcount(g)  #顶点数
ecount(g)  #边数
E(g)  #边的方向
E(g)$weight  #表示每条边的最大承载力（流量限制）
flow1 = graph.maxflow(g,1,8,E(g)$weight)  
flow1

结果中cut为割集，value为最大流，flow是具体流量