基于ICC聚类算法的市场状态预测模型

Posted 2021-07-25 XYQuantResearch

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了基于ICC聚类算法的市场状态预测模型相关的知识，希望对你有一定的参考价值。

导读

1、作为西学东渐--海外文献推荐系列报告第一百二十四篇，本文推荐了Pier Procacci和Tomaso Aste于2019年发表的论文《Forecasting Market States》

2、市场常常会呈现出不同的状态，比如牛市状态和熊市状态，但是对市场状态的识别与划分并没有统一的明确标准；同时在固定的划分方式下，对未来市场状态的预测也是一项重要的议题。本文基于ICC聚类算法，对市场状态进行识别和预测。

3、市场状态的识别：首先，本文基于ICC聚类算法（Inverse Covariance Clustering，逆协方差聚类），将100只股票的收益率序列作为输入变量，对历史上的市场状态划分为两类，分别定为牛市状态和熊市状态。从股票在不同状态下的平均收益来看，该方法具有较好的聚类效果。

4、市场状态的预测：之后，本文基于ICC聚类算法，对未来的市场状态进行预测，具体来讲，输入变量为过去24日的股票收益率，输出结果为下一个交易日的市场状态（牛市状态或熊市状态）。结果表明，本文方法对于未来市场状态的预测具有较高的准确率。

5、本文的方法实际上是利用收益率时间序列数据进行了技术面的市场状态预测，没有借助宏观变量、情绪变量等，方法较为纯粹，为技术面择时的投资者提供了新的思路。

风险提示：文献中的结果均由相应作者通过历史数据统计、建模和测算完成，在政策、市场环境发生变化时模型存在失效的风险。

1、引言

市场并不总是呈现出同一种状态，而是存在着价格更有可能上涨的“牛市”时期和价格更有可能下跌的“熊市”时期。这些不同的市场状态通常被是由一系列宏观经济变量、市场变量和情绪变量所决定的。本文提出了一种新的方法来定义、分析和预测市场状态。

众多学术文献曾提出过各种时间序列模型，以试图捕捉不同的市场状态。其中较受欢迎的方法是TAR模型（Tong，1978）和马尔可夫转换模型（Hamilton，1989）：TAR模型试图在时间序列过程中估计“结构性断点”；马尔可夫转换模型通常根据马尔可夫链进行建模，利用建模得到的状态变量来反映市场状态的变化。然而，TAR模型在应用过程中存在一定问题：当经济时间序列发生结构性中断时，TAR模型不能确定地建立起来；而且对重大经济事件的先验知识可能导致推断偏差（Campbell等，1997）。而马尔可夫转换模型则面临着维数灾难的问题：特别是对于更复杂的动态变化（Hamilton，1989），则需要依赖变分推断方法或MCMC方法（Tsay，2005；Kim和Nelson，1999）。这意味着在多元变量的情况下，尤其是从相关性结构中提取切换信息时，将难以进行相应的估计。

其他方法侧重于将观察结果聚类成组：根据某些比较标准来发现“相似的”数据对象。时间序列聚类的研究主要分为两类：子序列聚类和点聚类。子序列聚类涉及数据滑动窗口的聚类，通常以发现重复模式为目标，例如动态时间弯曲方法（Liao，2005）、层次方法（Neville-Manning和Witten，1997）或模式发现方法（Ren等，2017）。相反，在点聚类方法中，在各个时间点t上的多元观测值都被分类到相应的聚类中。最常见的方法是通过距离度量来实现的（Grabarnik和Särkkä，2001；Focardi和Fabozzi，2004；Zolhavarih等，2014；Hendricks等，2016；Hallac等，2016）。

在多元的情况下，市场的不同状态不仅反映在收益和损失上，也反映在价格的相对动态上。事实上，牛市和熊市存在的相关性结构变化表明这些市场状态存在结构性差异。为方便起见，业内最常见的方法是假设相关性结构是平稳的（Black和Litterman，1992；Duffie和Pan，1997）。然而，股票之间的相关性不是恒定不变的，而是会随时间变化而变化，（Lin等，1994 ；Ang和Bekaert，2002；Musmeci等，2016），其在市场剧烈波动期间大幅增加，尤其是在市场整体下行时（Ang和Chen，2002；Cizeau等，2010；Schmitt等，2013）。事实上，相关文献提出了一些方法来对时变相关性进行建模和预测。例如，Bollerslev (1990) 的广义自回归条件异方差模型 (GARCH模型) 或Engle (2002) 的动态条件相关模型 (DCC模型)。然而，由于维数灾难的问题，这些模型通常无法应用于多个资产：随变量数量增加，参数数量会呈超线性增加（Danielsson，2011）。其他方法根据滚动窗口计算时变相关矩阵，然后聚焦于时变相关矩阵的变化，例如RiskMetrics等估计量（Longerstaey和Spencer，1996；Lee和Stevenson，2003）。然而，这些方法只使用小部分数据，这会导致估计量有较大差异；并且在高维情况下，可能会导致不确定的估计（Laloux等，1999）。

Hallac等人（2017）提出了一种名为TICC（Toeplitz Inverse Covariance Clustering，即Toeplitz逆协方差聚类）的聚类算法，该算法最初是针对电动汽车提出的，通过与参考稀疏精度矩阵（逆协方差矩阵）相关的似然测度构建状态分类。然而，他们的方法并没有孤立地考虑每一个观测对象，而是将较短的子序列进行了聚类，使得在子序列上构造的协方差矩阵能够提供跨时间偏相关的信息。在这种情况下，通过对每个状态的精度矩阵添加Toeplitz约束，将跨时间偏相关系数约束为常数，从而实现协方差的平稳性。尽管作者考虑的数据结构与金融中的嘈杂数据有所不同，但是从金融学的角度来看，该方法仍有许多吸引人的特点。

本文在Hallac等人（2017）的基础上提出了一种类似的基于协方差的聚类方法。然而，我们只考虑单一的观测值，并没有在精度矩阵上强制使用Toeplitz结构。因此，我们称这种方法为ICC （Inverse Covariance Clustering，逆协方差聚类）。与Hallac等人（2017）类似，我们对市场状态之间的频繁切换进行惩罚，以此来加强时间上的一致性。与Hallac等人方法的另一个区别是，我们没有直接最大化似然度，而是根据马氏距离将状态分类（De Maess- chalck等，2000）。我们在金融时间序列的背景下实证了这种方法，并对稀疏性和时间一致性所起的作用进行了详细的分析，同时评估了聚类的重要性。最后，我们证明了聚类分类可以用于样本外的一步预测。

2、聚类

如上所述，本文的主要目标是在控制时间一致性的同时，有效地将有噪声的多元时间序列聚类为不同状态。在第一个实验中，我们考虑了1995年1月2日至2015年12月31日之间的整个数据集，并将其分为两种市场状态。为了探究算法中每个模块的作用，以及其与传统基准方法之间的区别，我们共研究了五个模型：

(a) ICC模型——稀疏精度矩阵和时间一致性

(b) ICC模型——全精度矩阵和时间一致性

(d) ICC模型——全精度矩阵

(e) 高斯混合模型——全协方差

我们通过网格搜索优化了时间一致性参数：在本文的两个实验中，对于ICC稀疏模型(a)，γ=16；对于ICC全模型(b)，γ=14.7。实验得到的两个参考精度矩阵和有344个非零项（依赖网络边），其中142个是两种状态共有的，表现出一定的差异程度，但两种市场状态之间也存在显著的重叠。分配给每个聚类的样本数分别为：聚类1为3295，聚类2为1704。图表1用不同颜色的背景展示了两个聚类。我们可以观察到有较好的连续性。例如，聚类1中平均的连续天数是25.3天。我们还注意到，聚类1（蓝色背景）倾向于与市场价格上涨的时期有关，而聚类2（橙色背景）在金融危机和市场低迷时期出现得更多。可以发现该方法自动将“牛市”时期（正平均回报）分配给聚类1，将“熊市”时期（负平均回报）分配给聚类2。例如，我们可以在图1(a)中观察到：2001-2002年互联网泡沫危机期间的52个连续观测数据被归入熊市聚类2，同时2007-2008年全球金融危机期间的211个连续观测数据也被归入熊市聚类2。从图1(b)我们可以观察到，牛市聚类1所有股票的平均回报为正数，而熊市聚类2的平均回报则为负数。此外，两种聚类的标准差也不同。

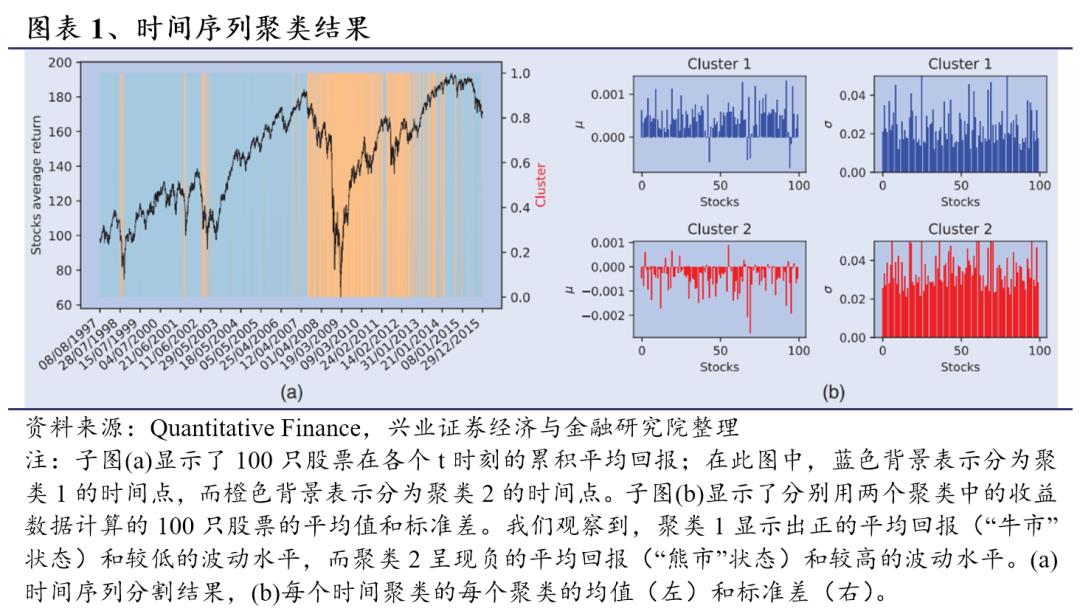
为了比较风险调整收益，我们计算了每个聚类中每只股票的夏普比率：牛市聚类的平均年化夏普比率为1.2，第5百分位数和第95百分位数分别为0.84和1.78，而熊市聚类的平均夏普比率为-0.96，第5百分位数和第95百分位数分别为-1.03和-0.24。因此，这两个聚类有着非常不同的风险收益情况。图表2展示了这两个聚类中100只股票的夏普比率，其中蓝色柱代表根据聚类1中的对数回报计算的夏普比率，而红色柱代表根据聚类2中的对数回报计算的夏普比率。为了验证结果的稳健性和通用性，我们对另外一组随机的100只股票计算夏普比率，并将该过程重复了100次。对于所有重新抽样的股票组合，我们发现均可产生关于牛市和熊市的连续性聚类结果，其中至少75%的股票在牛市状态下夏普比率大于零，且在熊市状态下夏普比率显著小于零。在100次重采样中，两个聚类的平均天数分别为3451和1293。

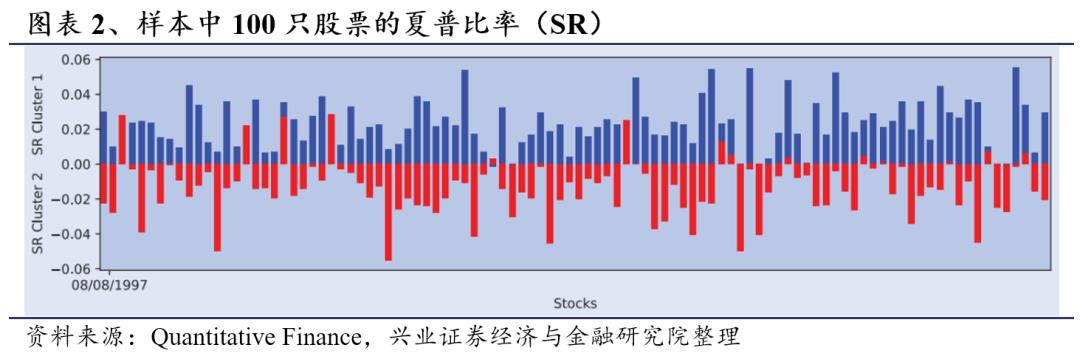
为了评估稀疏性和时间一致性的作用，我们对“备选”ICC模型(b) - (d)和GMM模型(e)进行了相同的分析。

图表3展示了100次重采样中在两个聚类中具有正/负夏普比率的股票数量。在表格中，每一对数据代表的是在牛市中夏普比率为正（左）和在熊市中夏普比率为负（右）的股票数量。我们发现，在没有时间一致性约束的情况下，两种ICC模型(c和d)均能进行有效分类。然而，当考虑时间一致性约束时，ICC全模型(b)受到约束的影响较为显著，分类效果有所减弱，而ICC稀疏模型(a)提供了稳健的结果。就收益风险角度而言，GMM的聚类效果最差。

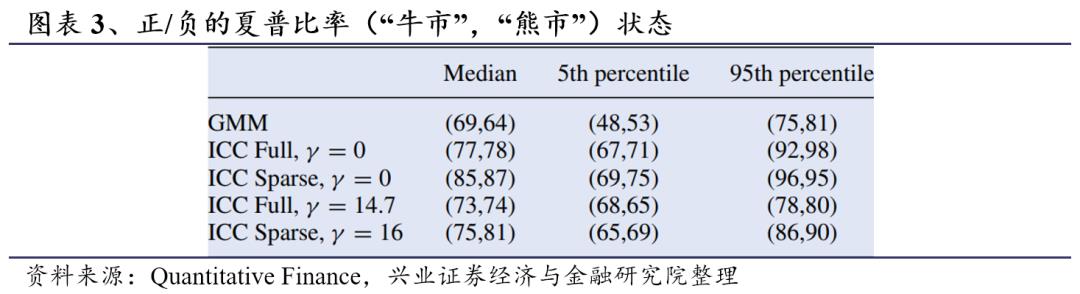
从时间一致性的角度来说，图表4展示了5个模型的聚类所产生的切换次数和分段长度。当没有时间一致性约束时（即模型(c)、(d)），ICC提供了较短的时间一致性结果。当被限制时间一致性时，ICC全模型(b)在不同样本间呈现出不同的时间一致性，有些在整个周期内只有几次切换，而另一些则有几百次切换。ICC稀疏模型(a)在整个周期中则有几百次切换，小于GMM (e)中切换次数的1/3。

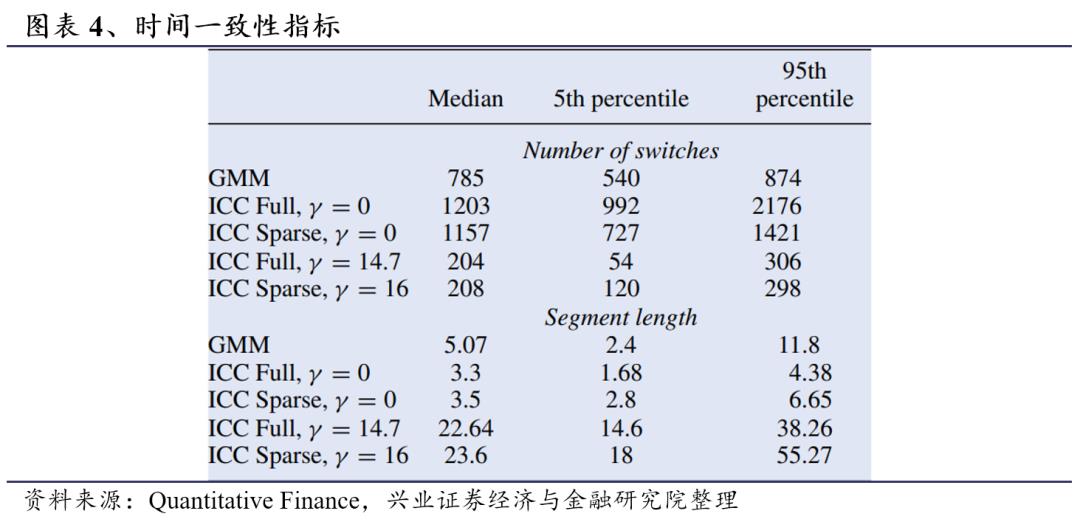
3、稀疏性的作用

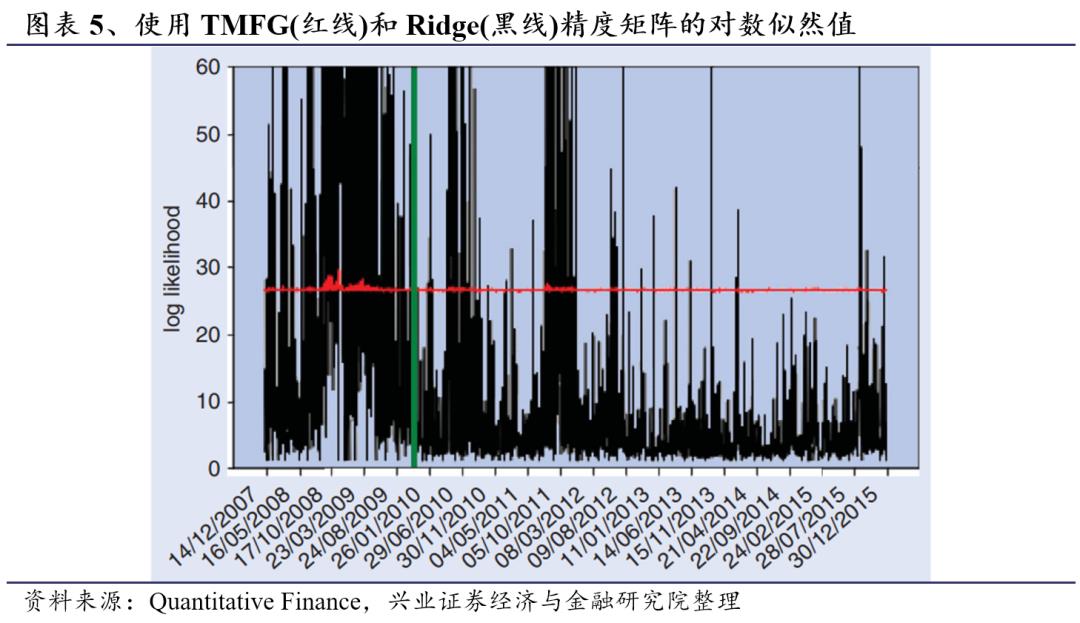
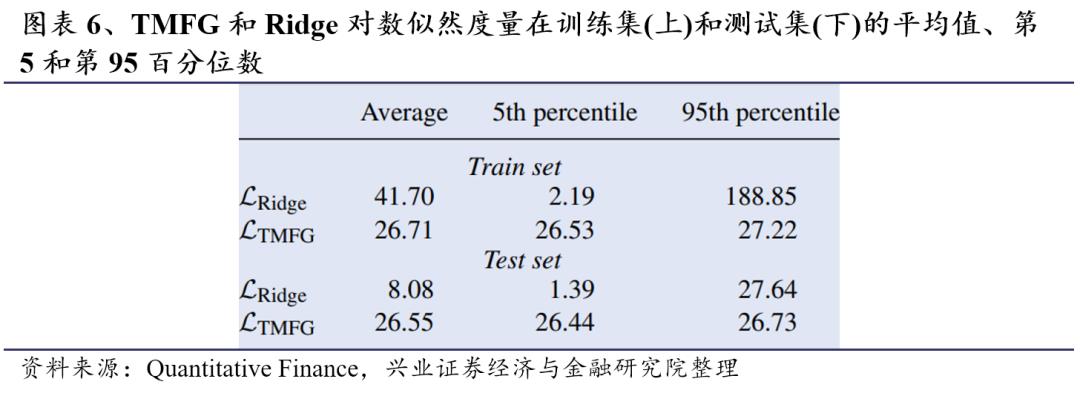
图表6显示了在训练集和测试集中计算的概率的平均值、第5百分位数和第95百分位数的详细信息。如上所述，TMFG-LoGo的似然度更稳定，TMFG-LoGo的第5和第95百分位数只变化了几个百分点，而Ridge的变化超过一个数量级。当考虑不同的q值时，我们在TMFG-LoGo和Ridge中发现了类似的结果。值得注意的是，Ridge的对数似然度在训练集和测试集上有很大的差异，这是过拟合的典型迹象。相反，TMFG表现出很小的差异，表明LoGo过程充当了拓扑惩罚。

4、预测

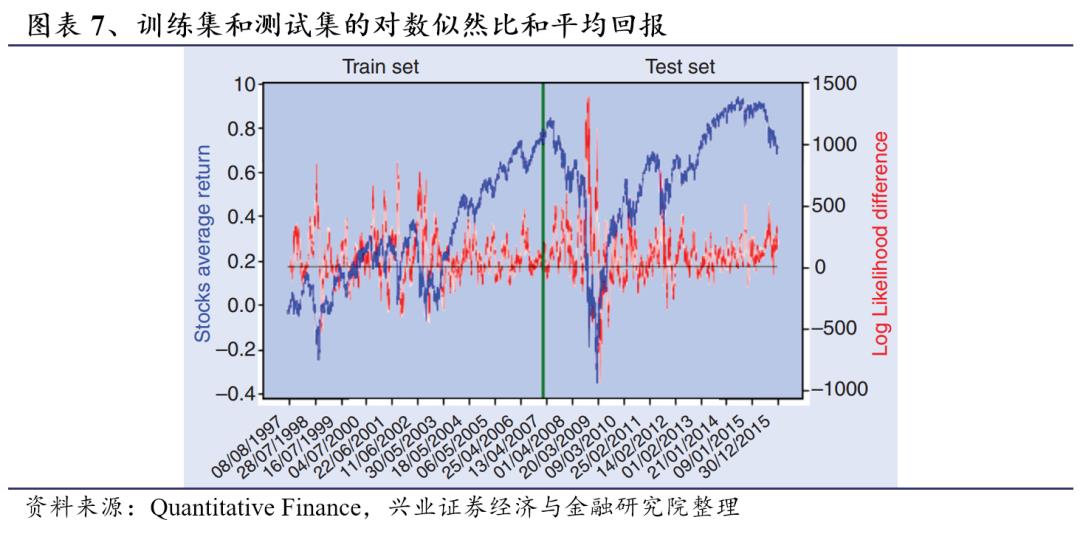
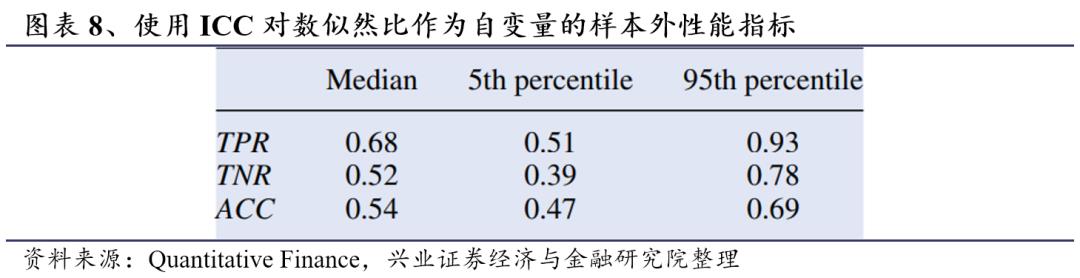
为了评估以上方法的效果，我们将测试集上的预测结果与在第一次实验的整个时间段内的分类结果进行了比较（见图表1）。我们使用了三个指标（Hastie等，2008）来评估我们分类方法的效果：真正例率TPR（True Positive Rate，正确归为聚类1的样本数除以归为聚类1的样本总数)，真负例率TNR（True Negative Rate，正确归为聚类2的样本数除以归为聚类2的样本总数）和准确率ACC（Accuracy，预测正确的样本数除以样本总数）。为了检验该方法的稳健性，我们对100只股票进行了随机重采样，并针对新的数据集进行了分类实验。我们重复这个过程100次，并计算了三个评价指标TPR、TNR和ACC，结果展示在图表8中。在重采样中获得了良好的ACC水平，只有第5百分位略低于50%。TPR在第5百分位时也高于50%，而TNR仅呈现良好的中位数结果，较低的第5百分位数值表明很难正确预测。这表明我们的方法有将样本过度分配到聚类1（牛市状态）的倾向。尽管如此，通过使用Aste和Di Matteo（2017）提出的超几何分布，我们验证了这些TNR在0.01水平上具有统计显著性，表明对熊市状态具有显著预测能力。需要强调的是，目前的预测没有进行进一步的优化，模型表现可以通过多种方式加以改进。但这超出了本文的初衷：本文更关注于方法的简单性，而不是一味追求效果。

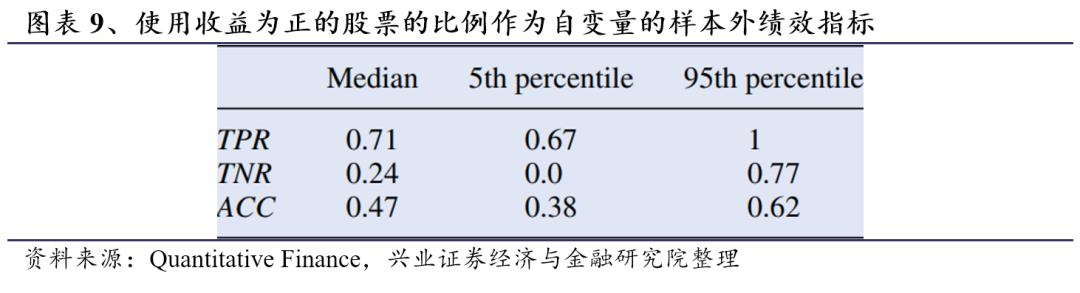
为了将上文的结果与基准方法进行对比，我们将时间t – 1时收益为正的股票的占比作为自变量，来估计方程3中的逻辑回归，从而将本文的ICC对数似然与关于相关性结构的信息简化版本进行比较。采用相同的估计方式，通过交叉验证得到阈值为0.61，结果见图表9。这种简化信息方法可以提供接近50%的中位数准确率，但与图表8中显示的ICC对数似然比的结果相比，该模型总体性能较差。

5、结论

在本文中，我们提出了一种新的方法来定义、识别、分类和预测市场状态。本文的方法具有准确性、直观性和较强的预测能力，并且能够处理高维数据。我们针对多元非平稳的金融数据集进行了两个实验，结果表明该方法在识别和预测数据集结构方面具有较强的有效性。实验使用了两个聚类和100个变量，我们也证实了类似的结果可以适用于更多或更少的变量；当使用三个或更多的聚类时，也会出现有趣的分类结果，本文选择两组只是为了简化问题。本文为使用多元分析预测股市回报的方法提供了新思路，也极大地简化了对“牛市”和“熊市”的解释。当然，在现实中，不止有两种市场状态，而且牛市和熊市的定义常常是模糊的。本文没有试图优化结果，而是更关注于简单性和可解释性，因此能够提供一个较大的开放性领域来完善本文的方法。我们还采用了几个可以在未来研究中修改的备选方法。例如，马氏距离是一个有效的方法；欧几里德距离和似然实验也可以产生不错的效果。此外，TMFG网络、其他信息过滤网络、其他稀疏化方法也是可以采用的方法。时间一致性也可以使用隐式马尔可夫方法来实行。通过逻辑回归来预测市场状态只是众多回归方法中简单的一个，本文选择它的原因是，它可能可以更好地利用我们状态结构的信息内容。所有这些方法的选择都是出于简单和直观的动机，因为本文方法的主要成就之一是计算效率，允许我们将该方法应用于高维数据集。进一步的研究将包括新的信息来源（如新闻、经济指标、情绪等）。

参考文献

[1] Ang, A.和Bekaert, G., International asset allocation with timevarying correlations. Rev. Financial Stud., 2002, 15, 1137–1187.

[2] Ang, A.和Chen, J., Asymmetric correlations of equity portfolios. J. Financ. Econ., 2002, 63, 443–494.

[3] Aste, T.和Di Matteo, T., Causality network retrieval from short time series. ArXiv preprint arXiv:1706.01954, 2017.

[4] Barfuss, W., Massara, G.P., di Matteo, T.和Aste, T., Parsimonious modeling with information filtering networks. Phys. Rev. E, 2016, 94, 062306.

[5] Bishop, C.M., Pattern Recognition和Machine Learning, 2006 (Springer-Verlag: New York).

[6]Black, F.和Litterman, R., Global portfolio optimization. Financ. Anal. J., 1992, 48, 28–43.

[7] Bollerslev, T., Modelling the coherence in short-run nominal exchange rates: A multivariate generalized ARCH model. Rev. Econ. Stat., 1990, 4, 498–505.

[8] Campbell, J.Y., Lo, A.W.和MacKinlay, A.C., The Econometrics of Financial Markets, 1997 (Princeton University Press: Princeton, NJ).

[9] Cizeau, P., Potters, M.和Bouchaud, J.P., Correlation structure of extreme stock returns. Quant. Finance, 2010, 1, 217–222.

[10] Danielsson, J., Financial Risk Forecasting: The Theory和Practice of Forecasting Market Risk with Implementation in R和Matlab, 2011 (Wiley-Blackwell: Hoboken).

[11] De Maesschalck, R., Jouan-Rimbaud, D.和Massart, D.L., The Mahalanobis distance. Chemometr. Intell. Lab. Syst., 2000, 50, 1–18.

[12] Duffie, D.和Pan, J., An overview of value at risk. J. Derivatives, 1997, 4, 7–49.

[13]Engle, R., Dynamic conditional correlation. J. Bus. Econ. Stat., 2002, 20, 339–350.

[14] Focardi, S.M.和Fabozzi, F.J., A methodology for index tracking based on time-series clustering. Quant. Finance, 2004, 4, 417–425.

[15] Friedman, J., Hastie, T.和Tibshirani, R.,稀疏模型inverse covariance estimation with the graphical lasso. Biostatistics, 2008, 9, 432–441.

[16] Grabarnik, P.和Särkkä, A., Interacting neighbour point processes: Some models for clustering. J. Stat. Comput. Simul., 2001, 68, 103–125.

[17] Hallac, D., Nystrup, P.和Boyd, S., Greedy Gaussian segmentation of multivariate time series. ArXiv e-prints, 2016.

[18] Hallac, D., Vare, S., Boyd, S.P.和Leskovec, J., Toeplitz inverse covariance-based clustering of multivariate time series data. CoRR, abs/1706.03161, 2017.

[19] Hamilton, J.D., A new approach to the economic analysis of nonstationary time series和the business cycle. Econometrica, 1989, 57, 357–384.

[20] Hastie, T., Tibshirani, R.和Friedman, J., The Elements of Statistical Learning, 2008 (Springer: New York).

[21] Hendricks, D., Gebbie, T.和Wilcox, D., Detecting intraday financial market states using temporal clustering. Quant. Finance, 2016, 16, 1657–1678.

[22] Kim, C.J.和Nelson, C., State-Space Models with Regime Switching: Classical和Gibbs-Sampling Approaches with Applications, 1999 (The MIT Press: Cambridge, MA).

[23] Laloux, L., Cizeau, P., Bouchaud, J.P.和Potters, M., Noise dressing of financial correlation matrices. Phys. Rev. Lett., 1999, 83, 1467–1470.

[24] Lauritzen, S.L., Graphical Models, 1996 (Oxford University Press: Oxford).

[25] Lee, S.和Stevenson, S., Time weighted portfolio optimisation. J. Prop. Investment Finance, 2003, 21, 233–249.

[26] Liao, W.T., Clustering of time series data – a survey. Pattern Recogn., 2005, 38, 1857–1874.

[27] Lin, W.L., Engle, R.和Ito, T., Do bulls和bears move across borders? International transmission of stock returns和volatility. Rev. Financ. Stud., 1994, 7, 507–38.

[28] Longerstaey, J.和Spencer, M., RiskMetrics Technical Document, J.P. Morgan/Reuters, 1996.

[29] Massara, G.P., di Matteo, T.和Aste, T., Network filtering for big data: Triangulated maximally filtered graph. CoRR, abs/1505.02445, 2015.

[30] Musmeci, N., Aste, T.和Di Matteo, T., What does past correlation structure tell us about the future? An answer from network filtering. ArXiv e-prints, 2016.

[31] Musmeci, N., Nicosia, V., Aste, T., Di Matteo, T.和Latora, V., The multiplex dependency structure of financial markets. Complexity, 2017, 2017, 13.

[32] Nevill-Manning, C.G.和Witten, I.H., Identifying hierarchical structure in sequences: A linear-time algorithm. J. Artif. Intell. Res., 1997, 7, 67–82.

[33] Neyman, J.和Pearson, E.S., IX. On the problem of the most efficient tests of statistical hypotheses. Philos. Trans. R. Soc. London A: Math. Phys. Eng. Sci., 1933, 231, 289–337.

[34] Ren, L., Wei, Y., Cui, J.和Du, Y., A sliding window-based multistage clustering和probabilistic forecasting approach for large multivariate time series data. J. Stat. Comput. Simul., 2017, 87, 2494–2508.

[35] Schmitt, T.A., Chetalova, D., Schäfer, R.和Guhr, T., Nonstationarity in financial time series: Generic features和tail behavior. EPL (Europhys. Lett.), 2013, 103, 58003.

[36] Sharpe, W.F., Mutual fund performance. J. Bus., 1966, 39, 119–138.

[37] Sharpe, W.F., The Sharpe ratio. J. Portf. Manag., 1994, 21, 49–58.

[38] Tong, H., On a threshold model. In Pattern Recognition和Signal Processing, edited by C. H. Chen, 1978 (Sijthoff和Noordhoff: Amsterdam).

[39] Tsay, R., Analysis of Financial Time Series, 2nd ed., 2005 (Wiley: Hoboken, NJ).

[40] Viterbi, A., Error bounds for convolutional codes和an asymptotically optimum decoding algorithm. IEEE Trans. Inf. Theory, 1967, 13, 260–269.

[41] Zolhavarieh, S., Aghabozorgi, S.和Wah Teh, Y., A review of subsequent time series clustering. Sci. World J., 2014, 2014, 312521.

风险提示：文献中的结果均由相应作者通过历史数据统计、建模和测算完成，在政策、市场环境发生变化时模型存在失效的风险。