数据库原理-第6章：Armstrong公理-模式的分解

Posted 2021-07-24 可能自洽

1.数据依赖的公理系统

1.1 Armstrong 公理

对于R〈U，F〉，X，Y，Z是属性集，F是函数依赖集。
自反律(reflexivity)：若Y $\subseteq$ X $\subseteq$ U， 则X→Y为F所蕴含。
增广律(augmentation)：若X→Y为F所蕴含，且Z $\subseteq$ U，则XZ→YZ为F所蕴含。
传递律(transitivity)：若X→Y，Y→Z为F所蕴含，则 X→Z 为F所蕴含。

由Armstrong公理导出的推理规则

合并律(union rule)：若X→Y，X→Z，则X→YZ
分解律(decomposition rule)：若X→Y，Z $\subseteq$ Y，则X→Z。 或者，若 X→YZ ，则X→Y，X→Z
伪传递律：若X→Y，WY→Z，则WX→Z

1.2 求属性集的闭包

例1 R< U, F >, U = (A, B, C, G, H, I), F = {A→B, A→C, CG→H, CG→I, B→H},计算 $(AG{)}_F^{+}$

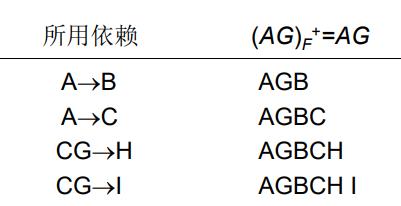
所以， $(AG{)}_F^{+}=AGBCHI$

例2 R< U, F >, U = (A, B, C, D, E), F = {AB→C, B→D, C→E, CE→B, AC→B}, 计算 $(AB{)}_F^{+}$

1.3 求最小函数依赖集

例 R< U, F >, U = (A, B, C, D, E), F = {A→B, BC→E, ED→AB},求等价于F的最小函数依赖集 $F_{min}$

①单属性化，得到F={A→B, BC→E, ED→A, ED→B}

②无冗余化，得到F={A→B, BC→E, ED→A}

A→B

令G=F-{A→B}={BC→E, ED→A, ED→B}
因为 $B\notin A_G^{+}$
所以A→B不冗余

BC→E

令G=F-{BC→E}={A→B, ED→A, ED→B}
因为 $E\notin B{C}_G^{+}$
所以BC→E不冗余

ED→A

令G=F-{ED→A}={A→B, BC→E, ED→B}
因为 $A\notin E{D}_G^{+}$
所以ED→A不冗余

ED→B

令G=F-{ED→B}={A→B, BC→E, ED→A}
因为 $B\in E{D}_G^{+}$
所以ED→B冗余

③既约化

BC→E

去掉属性B，因为 $E\notin C_F^{+}=C$ ，所以不能去掉
去掉属性C，因为 $E\notin B_F^{+}=B$ ，所以不能去掉

ED→A

去掉属性E，因为 $A\notin D_F^{+}=D$ ，所以不能去掉
去掉属性D，因为 $A\notin E_F^{+}=E$ ，所以不能去掉

④综上， F m i n = { A → B , B C → E , E D → A } F_{min}=\\{A→B, BC→E, ED→A\\} Fmin​={A→B,BC→E,ED→A}

2.模式分解等价的两个标准

例 对于关系模式SL（Sno， Sdept， Sloc），同一个系的学生住在一起，SL中有下列函数依赖：Sno→Sdept, Sdept→Sloc, Sno→Sloc, 已知SL∈2NF，该关系模式存在插入异常、删除异常、数据冗余度大和修改复杂的问题。

2.1 无损分解

将SL分解为下面二个关系模式：
ND(Sno, Sdept)
NL(Sno, Sloc)
分解后的关系：

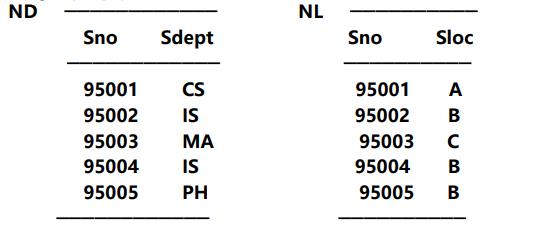
具有无损连接性，但未持函数依赖

2.2 保持函数依赖

将SL分解为下面二个关系模式：
ND(Sno, Sdept)
DL(Sdept, Sloc)
既具有无损连接性，又保持了函数依赖

2.3 判断对关系模式的一个分解是否与原关系模式等价的标准

（1）分解具有无损连接性

如果一个分解具有无损连接性，则它能够保证不丢失信息。

（2）分解要保持函数依赖

如果一个分解保持了函数依赖，则它可以减轻或解决各种异常情况。

（3）分解既要保持函数依赖，又要具有无损连接性

分解具有无损连接性和分解保持函数依赖是两个互相独立的标准。具有无损连接性的分解不一定能够保持函数依赖。同样，保持函数依赖的分解也不一定具有无损连接性。