4.5 希尔排序

Posted 2021-04-02 极夜编程

4.5 希尔排序

 

希尔排序(Shell Sort)

希尔排序本质上是直接插入排序的升级版。对于插入排序而言，在大多数元素已经有序的情况下，工作量会比较小。这个结论很明显，如果一个数组大部分元素都有序，那么数组中的元素自然不需要频繁地进行比较和交换。

如何能够让待排序的数组中大部分元素有序呢？需要对原始数组进行“预处理”，使得原始数组的大部分元素变得有序。采用“分组”的方法，可以将数组进行一定程度地“粗略调整”。

例如一个有8个数字组成的无序序列，进行升序排序。

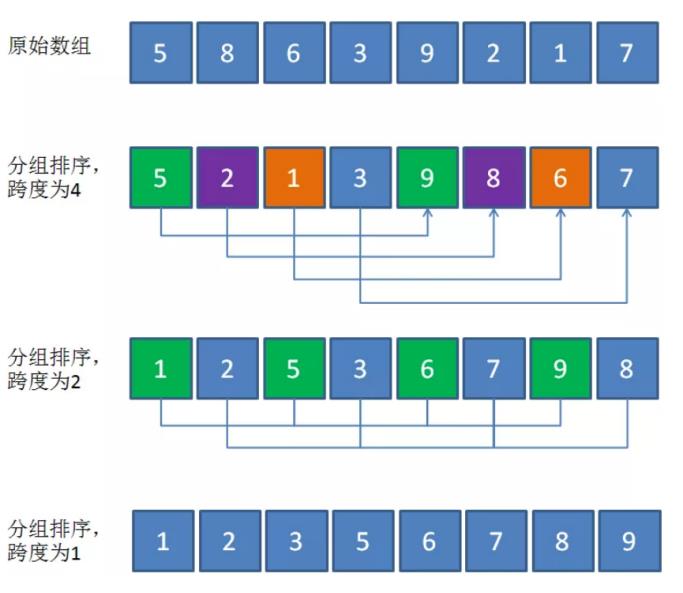
分组，即让元素两两一组，同组两个元素之间的跨度为数组总长度的一半，也就是4。

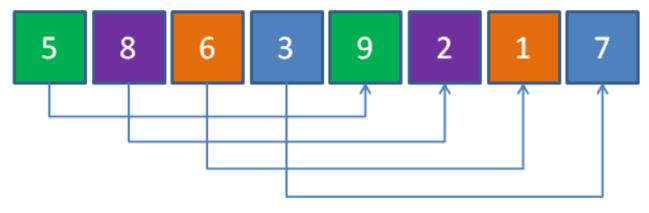
接着让每组元素进行独立排序，排序方式使用直接插入排序即可。由于每一组的元素数量很少，所以插入排序的工作量很少。

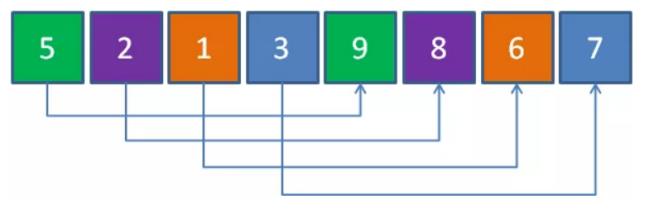
这样一来，仅仅经过几次简单的交换，数组整体的有序程序得到了显著提高，使得后续再进行直接插入排序的工作量大大减少。

但是这样还不算完，还可以进一步缩小分组跨度，重复上述工作。把跨度缩小为原先的一半，也就是跨度为2，重新对元素进行分组。

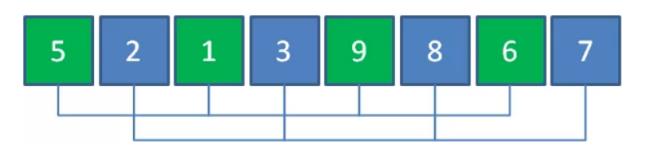
继续让每组元素进行独立排序。

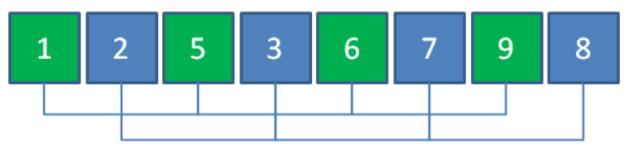
此时数组的有序程度进一步提高。最后将分组跨度再缩小一半，也就是跨度为1，也就是等同于做直接插入排序。经过之前的一系列粗略调整，直接插入排序的工作量减少了很多。

现在重新梳理一下刚才一系列的过程：

希尔排序的发明者是计算机科学家Donald Shell。希尔排序中说使用的分组跨度被称为希尔排序的增量。增量的选择可以有很多种，最朴素的就是Donald Shell在发明希尔排序时所提出的逐步折半的方法。

 

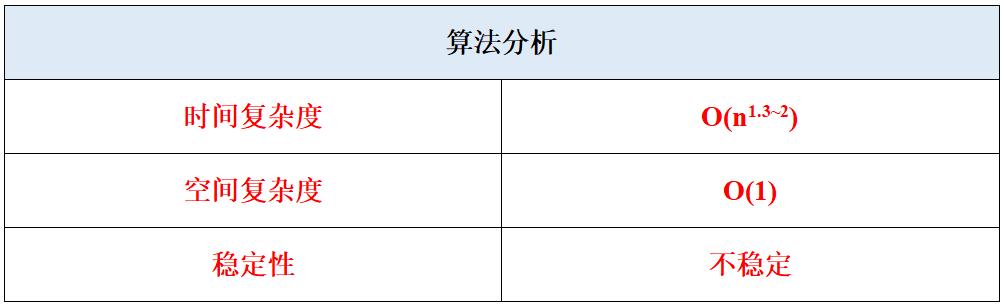
算法分析

希尔排序利用分组粗略调整的方式减少了直接插入排序的工作量，使得算法的平均时间复杂度低于O(n²)。但是在某些极端情况下，希尔排序的最坏时间复杂度仍然是O(n²)，甚至比插入排序更慢。

例如这样的数组：

无论是以4为增量，还是以2为增量，每组内部的元素都没有任何交换。直到增量缩减为1，数组才会按照直接插入排序的方式进行调整。

对于这样的数组，希尔排序不但没有减少直接插入排序的工作量，反而白白增加了分组操作的成本。

这是因为每一轮希尔增量之间都是等比的，这就导致了希尔增量存在盲区。为了避免这样的极端情况，科学家发明了许多更为严谨的增量方式。其中最具有代表性的是Hibbard增量和Sedgewick增量。

1. Hibbard增量序列：1, 3, 7, 15, ...

通项公式为2^k - 1。利用这种增量方式的希尔排序，最坏时间复杂度是O(n^3/2)。

2. Sedgewick增量序列：1, 5, 19, 41, 109, ...

通项公式为9*4^k - 9*2^k + 1或者4^k - 3*2^k + 1。利用这种增量方式的希尔排序，最坏时间复杂度是O(n^4/3)。

这两种增量方式的时间复杂度需要很复杂的数学证明，有些是人们的大致猜想。

【视频讲解】

Play