最优贸易（spfa）

Posted 2021-07-24 SSL_LKJ

最优贸易

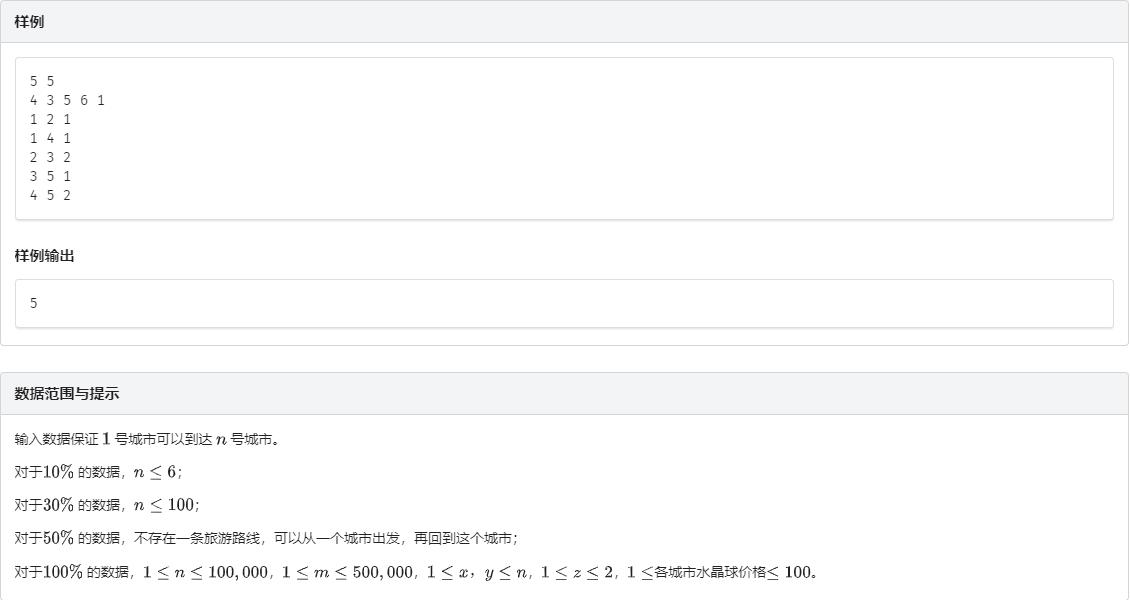
解题思路

用两个spfa
第二个要倒置

AC代码

#include<iostream>
using namespace std;
#define N 1000005
#define M 5000005
int n,m,x,y,z,tot1,tot2,head,tail,b[M],c[N],w[N],head1[M],head2[M],maxn[N],minn[N];
struct stu
{
	int to,next,w;
}a1[M],a2[M];
void add1(int x,int y)//邻接表1号
{
	tot1++;
	a1[tot1].to=y;
	a1[tot1].next=head1[x];
	head1[x]=tot1;
}
void add2(int x,int y)//邻接表2号（要倒置）
{
	tot2++;
	a2[tot2].to=y;
	a2[tot2].next=head2[x];
	head2[x]=tot2;
}
void spfa1(int o)
{
	minn[o]=w[o];//初值
    head=0;tail=1;
	b[1]=o;c[o]=1;
    do
    {
        head=head%N+1;//循环队列，否则会炸
        int k=b[head];//方便
        for(int i=head1[k];i;i=a1[i].next)
         if(minn[a1[i].to]>min(minn[k],w[a1[i].to]))//松弛算法
          {
            minn[a1[i].to]=min(minn[k],w[a1[i].to]);
            if(c[a1[i].to]==0)//是否标记过，没有就将这个数进入队列
             {
            	tail++;
            	b[tail]=a1[i].to;
            	c[a1[i].to]=1;
             }
          }
    	c[k]=0;
    }while(head<tail);
}
void spfa2(int o)
{
	maxn[o]=w[o];//初值
    head=0;tail=1;
	b[1]=o;c[o]=1;
    do
    {
        head=head%N+1;//循环队列，否则炸
        int k=b[head];//方便
        for(int i=head2[k];i;i=a2[i].next)
         if(maxn[a2[i].to]<max(maxn[k],w[a2[i].to]))//松弛算法（注意符号）
          {
            maxn[a2[i].to]=max(maxn[k],w[a2[i].to]);
            if(c[a2[i].to]==0)//进入队列或不进入队列
             {
            	tail++;
            	b[tail]=a2[i].to;
            	c[a2[i].to]=1;
             }
          }
    	c[k]=0;
    }while(head<tail);
}
int main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		cin>>w[i];//每个地方的买和卖水晶球的钱
		minn[i]=2147483647;//赋大值
	}
	for(int i=1;i<=m;i++)
	{
		cin>>x>>y>>z;
		add1(x,y);
		add2(y,x);
		if(z==2)add1(y,x);//双向
		if(z==2)add2(x,y);//双向
	}
	spfa1(1);
	for(int i=1;i<=n;i++)//清零
	 c[i]=0;
	spfa2(n);
	m=0;
	for(int i=2;i<=n-1;i++)//找最大赚的钱
	 m=max(m,maxn[i]-minn[i]);
	cout<<m;
	return 0;
} 

谢谢