有向图缩点（强连通分量）

Posted 2021-07-24 SSL_LKJ

有向图缩点

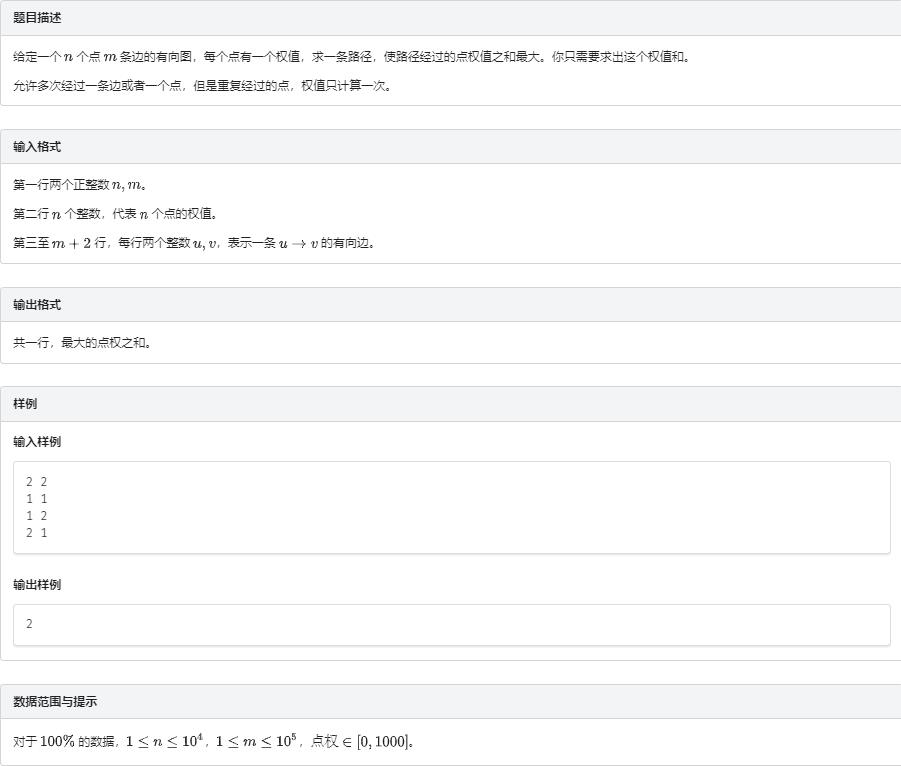
解题思路

这题先求强连通分量缩点
再进行dp

AC代码

#include<iostream>
#include<cstdio>
#include<queue>
using namespace std;
int n,m,T,TT,tot,tot1,top,ans; 
int f[10005],ru[10005],dfn[10005],low[10005],col[10005],sum[10005],num[10005],stak[10005],head[10005],head1[10005];
struct node
{
	int to,next;
}a[100005],b[100005];
void add(int x,int y)
{
	a[++tot]=(node){y,head[x]};
	head[x]=tot;
}
void add1(int x,int y)
{
	b[++tot1]=(node){y,head1[x]};
	head1[x]=tot1;
}
void Tarjan(int x)//求强连通分量缩点
{
	dfn[x]=low[x]=++T;
	stak[++top]=x;
	for(int i=head[x];i;i=a[i].next)
	{
		int v=a[i].to;
		if(!dfn[v])
		{
			Tarjan(v);
			low[x]=min(low[x],low[v]);
		}
		else if(!col[v])low[x]=min(low[x],low[v]);
	}
	if(dfn[x]==low[x])
	{
		col[x]=++TT;
		sum[TT]=num[x];
		while(stak[top]!=x)
		 sum[TT]+=num[stak[top]],col[stak[top--]]=TT;
		top--;
	}
	return;
}
void dp()
{
	queue<int>q;//队列
	for(int i=1;i<=tot;i++)if(!ru[i])q.push(i),f[i]=sum[i]; 
	while(!q.empty())
	{
		int x=q.front();
		q.pop();
		for(int i=head1[x];i;i=b[i].next)
		{
			int v=b[i].to;
			f[v]=max(f[v],f[x]+sum[v]);//用点u更新点v的f值
			ru[v]--;
			if(!ru[v])q.push(v);
		}
	}
	return;
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
	 scanf("%d",&num[i]);
	for(int i=1;i<=m;i++)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		add(x,y);
	}
	for(int i=1;i<=n;i++)
	 if(!dfn[i])Tarjan(i);
	for(int i=1;i<=n;i++)
	 for(int j=head[i];j;j=a[j].next)//枚举原图的所有边
	 {
	 	int v=a[j].to;
	 	if(col[i]!=col[v])//判断是否来自不同的强连通分量
	 	{
	 		add1(col[i],col[v]);//在新图中从点col[i]向col[v]连一条边
	 		ru[col[v]]++;//col[v]入度++
		}
	 }
	dp();
	for(int i=1;i<=n;i++)
	 ans=max(ans,f[i]);
	printf("%d",ans);
	return 0;
}

谢谢