Quantum State

Posted 2021-07-24 安徽思远

Qubit State

Notation

We need a name for this state. Let’s be unimaginative and call it 0. Similarly, there exists a qubit state that is certain to output a 1. We’ll call this 1. These two states are completely mutually exclusive. Either the qubit definitely outputs a 0, or it definitely outputs a 1. There is no overlap. One way to represent this with mathematics is to use two orthogonal vectors.

$$|0⟩=\left[\begin{array}{l}1\\ 0\end{array}\right]|1⟩=\left[\begin{array}{l}0\\ 1\end{array}\right]$$

With vectors we can describe more complex states than just $|0⟩$ and $|1⟩.$ For example, consider the vector
$$|q_0⟩=\left[\begin{array}{c}\frac{1}{\sqrt{2}}\\ \frac{i}{\sqrt{2}}\end{array}\right]$$

Since the states $|0⟩$ and $|1⟩$ form an orthonormal basis, we can represent any $2\mathrm{D}$ vector with a combination of these two states. This allows us to write the state of our qubit in the alternative form:
$$|q_0⟩=\frac{1}{\sqrt{2}}|0⟩+\frac{i}{\sqrt{2}}|1⟩$$

This vector, $|q_0⟩$ is called the qubit’s statevector, it tells us everything we could possibly know about this qubit. For now, we are only able to draw a few simple conclusions about this particular example of a statevector: it is not entirely $|0⟩$ and not entirely $|1⟩$. Instead, it is described by a linear combination of the two. In quantum mechanics, we typically describe linear combinations such as this using the word ‘superposition’.

Exploring Qubits with Qiskit (How to initiate quantum states)

from qiskit import QuantumCircuit, assemble, Aer
from qiskit.visualization import plot_histogram, plot_bloch_vector
from math import sqrt, pi
qc = QuantumCircuit(1) # Create a quantum circuit with one qubit

In our quantum circuits, our qubits always start out in the state $|0⟩.$ We can use the initialize() method o transform this into any state. We give initialize () the vector we want in the form of a list, and tell it which qubit(s) we want to initialize in this state:

qc = QuantumCircuit(1)  # Create a quantum circuit with one qubit
initial_state = [0,1]   # Define initial_state as |1>
qc.initialize(initial_state, 0) # Apply initialisation operation to the 0th qubit
qc.draw()  # Let's view our circuit

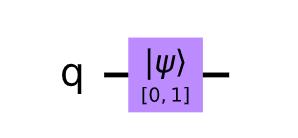
We can then use one of Qiskit’s simulators to view the resulting state of our qubit. To begin with we will use the statevector simulator, but we will explain the different simulators and their uses later.

svsim = Aer.get_backend('statevector_simulator') # Tell Qiskit how to simulate our circuit
qc = QuantumCircuit(1)  # Create a quantum circuit with one qubit
initial_state = [0,1]   # Define initial_state as |1>
qc.initialize(initial_state, 0) # Apply initialisation operation to the 0th qubit
qobj = assemble(qc)     # Create a Qobj from the circuit for the simulator to run
result = svsim.run(qobj).result() # Do the simulation and return the result
out_state = result.get_statevector()
print(out_state) # Display the output state vector

$$[\begin{array}{ll}0.+0.j& 1.+0.j]\end{array}$$

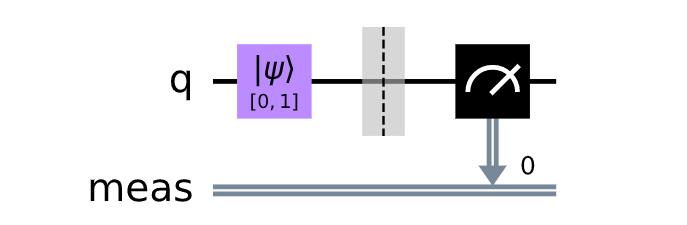
qc.measure_all()
qc.draw()

qobj = assemble(qc)
result = svsim.run(qobj).result()
counts = result.get_counts()
plot_histogram(counts)

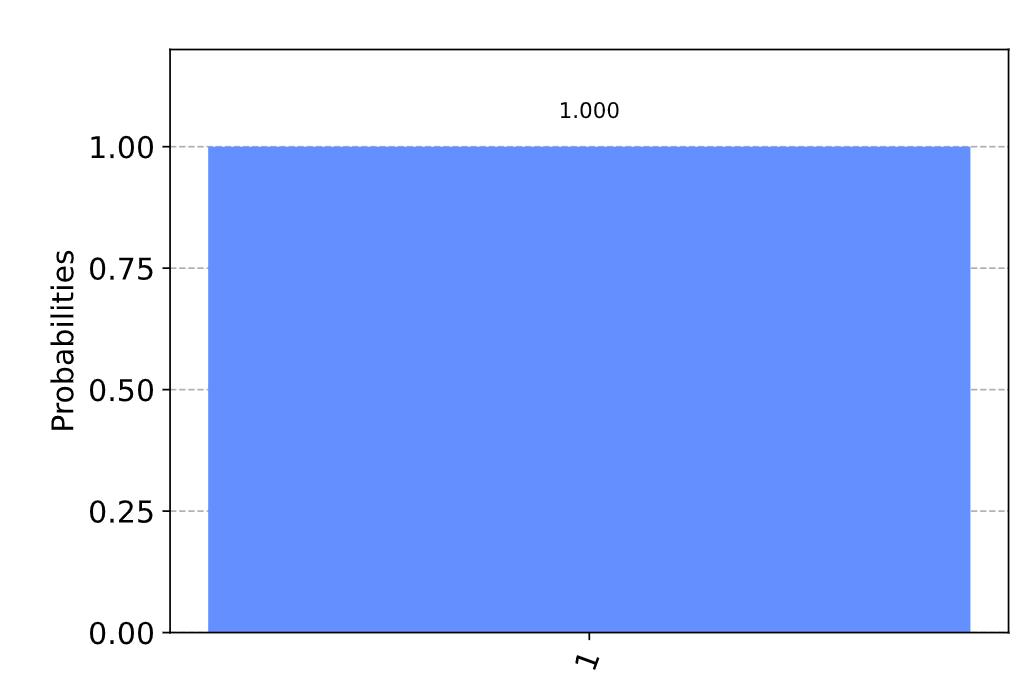
We can see that we (unsurprisingly) have a $100\%$ chance of measuring $|1⟩$. This time, let’s instead put our qubit into a superposition and see what happens. We will use the state $|q_0⟩$ from earlier in this section:
$$|q_0⟩=\frac{1}{\sqrt{2}}|0⟩+\frac{i}{\sqrt{2}}|1⟩$$
By initial_state, we can create a new quantum state.

initial_state = [1/sqrt(2), 1j/sqrt(2)]  # Define state |q_0>

qc = QuantumCircuit(1) # Must redefine qc
qc.initialize(initial_state, 0) # Initialize the 0th qubit in the state `initial_state`
qobj = assemble(qc)
state = svsim.run(qobj).result().get_statevector() # Execute the circuit
print(state)       

$$[\begin{array}{ccc}0.70710678+0.j& 0.& +0.70710678\mathrm{j}]\end{array}$$

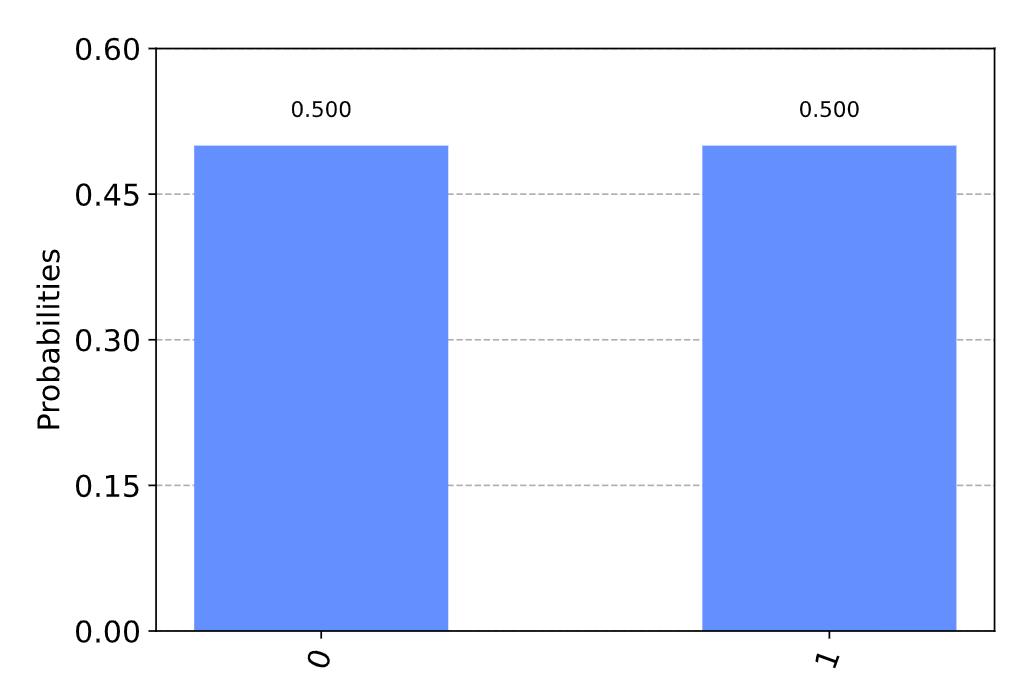
qobj = assemble(qc)
results = svsim.run(qobj).result().get_counts()
plot_histogram(results)

Measurement

Rule

There is a simple rule for measurement. To find the probability of measuring a state $|\psi ⟩$ in the state $|x⟩$ we do:
$$p(|x⟩)=|⟨x\mid \psi ⟩{|}^2$$

If we look at the state $|q_0⟩$ from before, we can see the probability of measuring $|0⟩$ is indeed $0.5$ :
$$\begin{array}{r}|q_0⟩\\ ⟨0\mid q_0⟩\\ \\ \\ {\left|⟨0\mid q_0⟩\right|}^2\end{array}$$

以上是关于Quantum State的主要内容，如果未能解决你的问题，请参考以下文章

Quantum State

Flutter 报错 DioError [DioErrorType.DEFAULT]: Bad state: Insecure HTTP is not allowed by platform(代码片段

七个办法只有一个有效：200 PORT command successful. Consider using PASV.425 Failed to establish connection.(代码片段

量子猴排（Quantum Bogo sort）

保留3D策略和Firefox Quantum，其他浏览器

GIT切换远程分支并拉取代码