Shor‘s algorithm
Posted 安徽思远
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Shor‘s algorithm相关的知识,希望对你有一定的参考价值。
周期函数:
f
(
x
)
=
a
x
m
o
d
N
f(x) = a^x \\bmod{N}
f(x)=axmodN
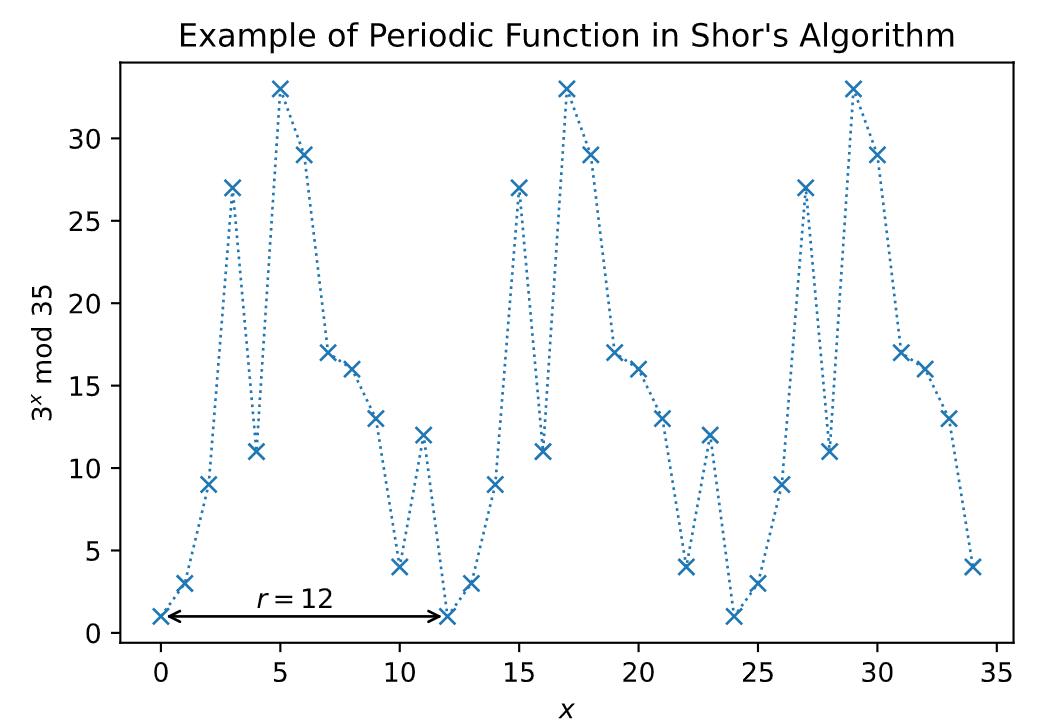
问题:如何找到一个周期函数的周期r?
Shor’s algorithm
Shor’s solution中函数U: U ∣ y ⟩ ≡ ∣ a y m o d N ⟩ U|y\\rangle \\equiv |ay \\bmod N \\rangle U∣y⟩≡∣aymodN⟩
接下来,我们可以多次作用U,便可以得到周期函数f的结果:
U
∣
1
⟩
=
∣
3
⟩
U
2
∣
1
⟩
=
∣
9
⟩
U
3
∣
1
⟩
=
∣
27
⟩
⋮
U
(
r
−
1
)
∣
1
⟩
=
∣
12
⟩
U
r
∣
1
⟩
=
∣
1
⟩
\\begin{aligned} U|1\\rangle &= |3\\rangle & \\\\ U^2|1\\rangle &= |9\\rangle \\\\ U^3|1\\rangle &= |27\\rangle \\\\ & \\vdots \\\\ U^{(r-1)}|1\\rangle &= |12\\rangle \\\\ U^r|1\\rangle &= |1\\rangle \\end{aligned}
U∣1⟩U2∣1⟩U3∣1⟩U(r−1)∣1⟩Ur∣1⟩=∣3⟩=∣9⟩=∣27⟩⋮=∣12⟩=∣1⟩
因此第一个想法便是构建叠加态,然后测量相同f(x)的x的叠加态。
So a superposition of the states in this cycle ( ∣ u 0 ⟩ ) (|u_0\\rangle) (∣u0⟩) would be an eigenstate of U:
∣ u 0 ⟩ = 1 r ∑ k = 0 r − 1 ∣ a k m o d N ⟩ |u_0\\rangle = \\tfrac{1}{\\sqrt{r}}\\sum_{k=0}^{r-1}{|a^k \\bmod N\\rangle} ∣u0⟩=r1k=0∑r−1∣akmodN⟩
This eigenstate has an eigenvalue of 1, which isn’t very interesting. A more interesting eigenstate could be one in which the phase is different for each of these computational basis states. Specifically, let’s look at the case in which the phase of the kth state is proportional to k:
∣ u 1 ⟩ = 1 r ∑ k = 0 r − 1 e − 2 π i k r ∣ a k m o d N ⟩ U ∣ u 1 ⟩ = e 2 π i r ∣ u 1 ⟩ \\begin{aligned} |u_1\\rangle &= \\tfrac{1}{\\sqrt{r}}\\sum_{k=0}^{r-1}{e^{-\\tfrac{2\\pi i k}{r}}|a^k \\bmod N\\rangle}\\\\[10pt] U|u_1\\rangle &= e^{\\tfrac{2\\pi i}{r}}|u_1\\rangle \\end{aligned} ∣u1⟩U∣u1⟩=r1k=0∑r−1e−r2πik∣akmodN⟩=er2πi∣u1⟩
∣ u s ⟩ = 1 r ∑ k = 0 r − 1 e − 2 π i s k r ∣ a k m o d N ⟩ U ∣ u s ⟩ = e 2 π i s r ∣ u s ⟩ \\begin{aligned} |u_s\\rangle &= \\tfrac{1}{\\sqrt{r}}\\sum_{k=0}^{r-1}{e^{-\\tfrac{2\\pi i s k}{r}}|a^k \\bmod N\\rangle}\\\\[10pt] U|u_s\\rangle &= e^{\\tfrac{2\\pi i s}{r}}|u_s\\rangle \\end{aligned} ∣us⟩U∣us⟩=r1k=0∑r−1e−r2πisk∣akmodN⟩=er2πis∣us⟩
We now have a unique eigenstate for each integer value of s where
0
≤
s
≤
r
−
1
0 \\leq s \\leq r-1
0≤s≤r−1. Very conveniently, if we sum up all these eigenstates, the different phases cancel out all computational basis states except
∣
1
⟩
|1\\rangle
∣1⟩:
1 r ∑ s = 0 r − 1 ∣ u s ⟩ = ∣ 1 ⟩ \\tfrac{1}{\\sqrt{r}}\\sum_{s=0}^{r-1} |u_s\\rangle = |1\\rangle r1s=0∑r−1∣us⟩=∣1⟩
Example:
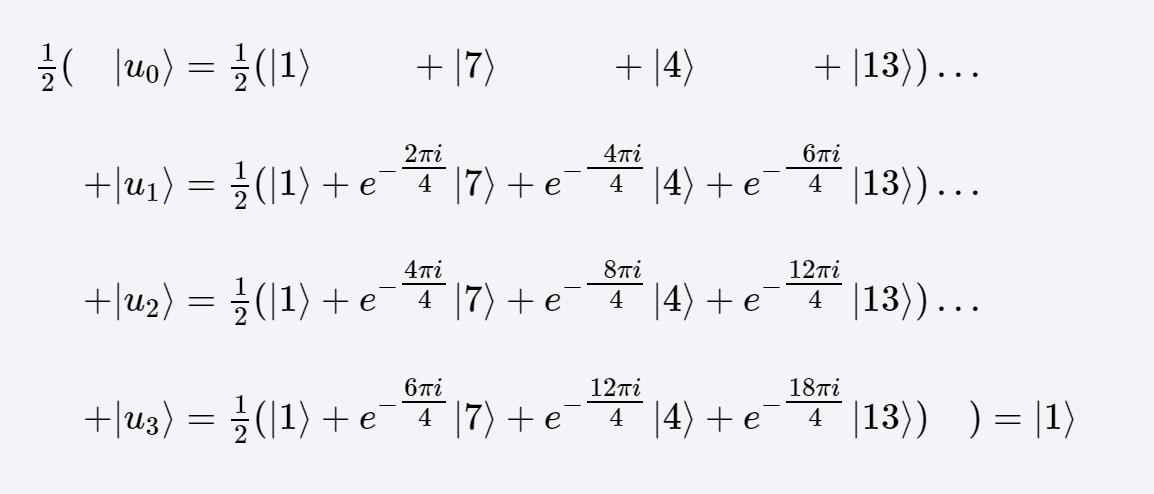
在通过U进行变化操作之后,我们得到的结果为:
∣
1
⟩
=
1
r
(
∣
u
0
⟩
+
∣
u
1
⟩
+
⋯
+
∣
u
r
−
1
⟩
)
|1\\rangle=\\frac{1}{\\sqrt{r}}\\left(\\left|u_{0}\\right\\rangle+\\left|u_{1}\\right\\rangle+\\cdots+\\left|u_{r-1}\\right\\rangle\\right)
∣1⟩=r