自动频率控制 AFC环--锁频环 FLL
Posted 者乎之类的
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了自动频率控制 AFC环--锁频环 FLL相关的知识,希望对你有一定的参考价值。
零、引言
锁相环路捕获时间直接与初始频差相关,初始频差越大,捕获时间越长。另一方面,锁相环的捕获带宽较小。因此,十分有必要在锁相环路前加一级锁频环路,将载波频偏控制在一较小范围内,便于锁相环的快速捕获。
一、最大似然频偏估计
设接收信号
r
(
t
)
=
sin
(
w
i
t
+
θ
i
)
+
n
(
t
)
{\\rm{r}}(t) = \\sin ({w_i}t + {\\theta _i}) + n(t)
r(t)=sin(wit+θi)+n(t)
在突发通信中,用于频偏估计的信号一般是导频信号。
设本地信号为:
v
o
q
(
t
)
=
cos
(
w
0
t
+
θ
0
)
{v_{oq}}(t) = \\cos ({w_0}t + {\\theta _0})
voq(t)=cos(w0t+θ0)
v
o
i
(
t
)
=
sin
(
w
0
t
+
θ
0
)
{v_{oi}}(t) = \\sin ({w_0}t + {\\theta _0})
voi(t)=sin(w0t+θ0)
相乘滤除倍频分量后得到含有载波频偏和相偏的IQ两路正交信号
I
(
t
)
=
cos
(
Δ
w
t
+
θ
)
+
n
i
(
t
)
I(t) = \\cos (\\Delta w{\\rm{t}} + \\theta ) + {n_i}(t)
I(t)=cos(Δwt+θ)+ni(t)
Q
(
t
)
=
sin
(
Δ
w
t
+
θ
)
+
n
i
(
t
)
Q(t) = \\sin (\\Delta w{\\rm{t}} + \\theta ) + {n_i}(t)
Q(t)=sin(Δwt+θ)+ni(t)
其中,
Δ
w
=
w
i
−
w
o
\\Delta w = {w_i} - {w_o}
Δw=wi−wo,
θ
=
θ
i
−
θ
o
\\theta = {\\theta _i} - {\\theta _o}
θ=θi−θo
那么可获得离散相位信息
x
~
k
=
arctan
(
Q
/
I
)
{\\tilde x_k} = \\arctan (Q/I)
x~k=arctan(Q/I)
那么连续相位信息
x
k
=
x
k
−
1
+
(
x
~
k
−
x
~
k
−
1
)
{x_{\\rm{k}}} = {x_{k - 1}} + ({\\tilde x_{\\rm{k}}} - {\\tilde x_{k - 1}})
xk=xk−1+(x~k−x~k−1) ----1式
现在再捋一下我们要干什么,我们是要得到频差信息,即
Δ
w
\\Delta w
Δw,我们现在有了xk,
而
x
k
=
2
π
k
T
s
Δ
f
+
θ
+
v
k
{x_k} = 2\\pi k{T_s}\\Delta f + \\theta + {v_k}
xk=2πkTsΔf+θ+vk
现在问题模型就是已知xk,估计
Δ
w
\\Delta w
Δw(
Δ
f
\\Delta f
Δf)和
θ
\\theta
θ
将1式写成向量形式
X
=
Δ
f
a
+
θ
b
+
V
X = \\Delta fa + \\theta b + V
X=Δfa+θb+V
X是服从高斯分布的随即向量
f
x
(
X
)
=
1
2
π
σ
N
e
−
1
2
σ
2
∣
∣
X
−
Δ
f
a
−
θ
∣
∣
2
{f_{\\rm{x}}}({\\bf{X}}) = \\frac{1}{{\\sqrt {2\\pi {\\sigma ^N}} }}{{\\rm{e}}^{ - \\frac{1}{{2{\\sigma ^2}}}}}||{\\bf{X}} - \\Delta fa - \\theta |{|^2}
fx(X)=2πσN1e−2σ21∣∣X−Δfa−θ∣∣2
对于剩余频差
Δ
f
\\Delta f
Δf和剩余相差
θ
\\theta
θ的最大似然估计
Δ
f
^
(
X
)
\\Delta \\hat f({\\bf{X}})
Δf^(X)和
θ
^
(
X
)
\\hat \\theta ({\\bf{X}})
θ^(X)的估计是使关于
Δ
f
\\Delta f
Δf和
θ
\\theta
θ的对数概率密度的梯度
∇
Δ
f
,
θ
log
f
x
(
X
)
{\\nabla _{\\Delta f,\\theta }}\\log {f_{\\rm{x}}}({\\bf{X}})
∇Δf,θlogfx(X)为零的解
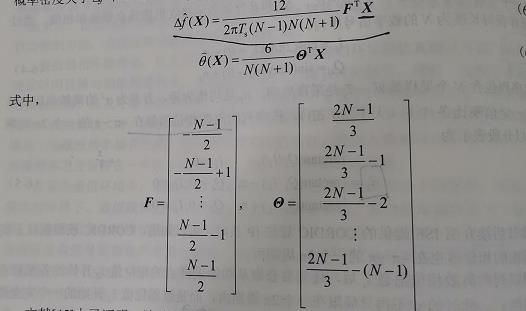
以上是关于自动频率控制 AFC环--锁频环 FLL的主要内容,如果未能解决你的问题,请参考以下文章