一阶二叉树模型
Posted 期权世界
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了一阶二叉树模型相关的知识,希望对你有一定的参考价值。
上海濡圣投资管理有限公司
二叉树模型是理解期权定价的最基础且最简单的模型。其实 Black-Scholes 期权定价模型等复杂的数学模型也可以在二叉树模型的基础上进行理解。在进行期权交易之前,虽然不一定要完全掌握 Black-Scholes 等复杂的理论,但至少要知道这些模型存在的意义,只有这样才能解决在实际交易过程中发生的诸多复杂问题和困难。
一阶二叉树模型
我们先了解在二叉树模型中最为简单的一阶二叉树模型。我们的最终目的是在既定的条件下求出期权现在(开始时点)的合理价格,然后才能判断期权是被高估还是被低估,因此求期权的合理价格就成为期权交易的基础。合理价格指交易公平原理下的价格,在经济学中用“有效市场中不存在无风险套利机会”表达“天下没有免费的午餐”这句话。
没有无风险套利机会意味着不存在与未来价格变动风险无关的稳定收益机会。因此,如果金融产品以“合理价格”交易就意味着该金融产品处于既没有被高估也没有被低估的公平定价的状态。若被高估则存在卖出该金融产品将获得确定收益的机会,若被低估则存在买入该产品将获得稳定收益的机会。
一阶二叉树模型只考虑开始和到期两个时点,即开始交易的时点和交易结束的时点(到期)。期权分为认购(买权)和认沽(卖权)两种类型,此处我们先考虑认购(买权)期权的情形。
认购期权到期的价值由到期时标的资产的价格和认购期权的行权价格决定。在这里先做一个假设:假设到期时标的资产价格较标的资产现价上涨(40%)或下跌 (-40%)。到期时标的资产的价格在现实中有上涨、下跌、价格不变三种可能。在本模型中做出了价格只有上涨和下跌两种情况,且提前知道上涨和下跌比例这样较为大胆的假设。如此的假设最初会显得很不现实,但以后将一阶二叉树模型推广到多阶二叉树模型,再推广到 Black-Scholes 模型后,我们会发现这些看似不现实的假设将逐渐符合真实市场环境。假定标的资产当前价格为 5000,认购期权是行权价为 5000 的平值期权,且是只能在到期后行权的欧式期权。再假定市场的利率为 20%。为了方便在这里假设存贷款利率同样为 20%。在这个假定下,如果到期时标的资产 价格上涨到 7000,则认购期权价值为 2000。如果标的资产价格下跌到 3000,则认购期权价值变为 0。
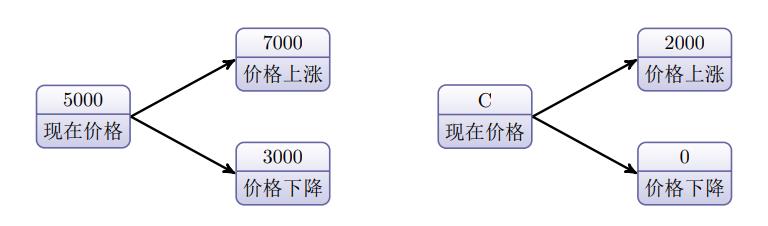
图:一阶二叉树模型
图中左边显示标的资产的现价和到期价格,右边显示尚不知合理价格(C)的当前时点认购期权价格和到期时的期权价值。认购期权到期时的价值在标的资产上涨时为 2000=7000−5000,在标的资产下跌时为 0。如何利用上面给定的条件和天下没有免费的午餐这个原理求得认购期权在当前时点的合理价格(C)?我们先来看一看金融产品的种类。
首先,从利率为 20%得知有债权产品。即投资该债券后无论何种情况都会在到期时得到 20%的利率。其次,有股票(标的资产)。投资该产品可能在到期时获得 40%收益,也可能出现-40%的亏损。最后,有认购期权。投资该期权到期时的价值为 2000 元或 0,这从直观上能判断该期权现价应为 0~2000 元的某个值。如果该期权现在以 3000 元的现价交易,很显然是被高估的。
适当地利用这三个产品,组成一个无论标的资产价格上涨或下跌都能获得确定收益的投资组合。股票和认购期权的到期价值以相同方向变动,因此可以判断,要想获得与到期状态无关的收益必须要持有股票和期权相反的头寸。买入股票需卖出认购期权,卖出股票(卖出融券)则要买入认购期权才能在到期时获得与到期状态无关的确定收益,即标的资产和认购期权的价格要相反。若两个产品都以相同方向买入,则无法获得独立于到期时标的资产价格状态的确定收益。因此这里我们先选择买入股票、卖出认购期权。
在这种情况下,买入和卖出股票、期权的数量将变得非常重要。要知道,股票买入量和认购期权卖出量之间存在一定的相关性,如果一边显著多于与或少于另一边,将无法获得预期的收益。虽然暂时还未知,但两者间买入量和卖出量的比例是非常重要的变量。我们暂且将该变量的名字定义为Δ。即买入Δ份的股票,同时卖出一份认购期权合约。这个组合的到期收益根据股票价格的变化分为上涨和下跌两种情 形。如果到期后标的资产价格上涨,则到期收益为Δ×7000−2000。如果到期后标的资产价格下跌,则到期收益为Δ×3000−0。即求无论发生任何情况都能得到期权益相同的Δ值,该值由Δ×7000−2000=Δ×3000-0 方程得出。
买入Δ份的股票,同时卖出一份认购期权合约。这个组合的到期收益根据股票价格的变化分为上涨和下跌两种情 形。具体如图所示,即求无论发生任何情况都能得到期权益相同的Δ值,该值由Δ×7000−2000=Δ×3000-0 方程得出。
图:到期的价值
由于我们是期权卖出方,因此该方程中没有认购期权的价格。解该方程得Δ=0.5,这就意味着买入 0.5 份股票、卖出 1 份认购期权后,,到期时标的资产价格无论是上涨还是下跌,该组合到期收益都为 0.5×7000−2000=0.5×3000=1500 元。当然,在实际交易中我们不能交易 0.5 份股票,但为了计算方便我们在这里假定允许以小于 1 的份额进行交易。
至此,我们求出了构建独立于标的资产价格变动风险而提供稳定权益的投资组合所需的股票和认购期权的买入/卖出比例 Δ。为了求出最终所要的认购期权的合理价格,我们再一次从“天下没有免费的午餐”这个浅显的道理出发去进行分析。假设当前的投资组合是买入 0.5 份股票、卖出 1 份认购期权,且该组合在到期时总是拥有 1500 元的价值。在金融市场上,还有一种产品在到期时不管市场情况如何都拥有确定的价值,这就是债券。买入债券后总能在到期时获得一定的债券收益(利息)。因此,不存在必须让到期价值相同的两类投资的当前价格相同。这个价格可由债券利息轻松求出。当利率为 20%时,要想获得到期价值为 1500 元,我们只需在当前时点购买 1500÷(1+0.2)=1250 元的债券。
以上是关于一阶二叉树模型的主要内容,如果未能解决你的问题,请参考以下文章