一文了解贪心算法和回溯算法在前端中的应用

Posted 2021-07-23 星期一研究室

一文了解贪心算法和回溯算法在前端中的应用

• 一、贪心算法
• • 1、贪心算法是什么？
  • 2、应用场景
  • 3、场景剖析：零钱兑换
• 二、回溯算法
• • 1、回溯算法是什么？
  • 2、什么问题适合选用回溯算法解决？
  • 2、应用场景
  • 3、场景剖析：全排列
• 三、贪心算法常见应用
• • 1、leetcode 455：分发饼干
  • 2、leetcode 122：买卖股票的最佳时机
• 四、回溯算法常见应用
• • 1、leetcode 46：全排列
  • 2、leetcode 78：子集
• 五、写在最后

在我们日常的生活中，经常会碰到贪心算法和回溯算法的应用场景。比如，贪心算法常应用于最少硬币找零问题，分数背包等问题。而回溯算法常用于迷宫求解、N皇后等问题。这两种各有各的优点，也各有各的不足。

在下面的这篇文章中，将讲解贪心算法和回溯算法的常见应用场景，以及分析高频 leetcode 算法题。

一起来学习⑧📖

一、贪心算法

1、贪心算法是什么？

• 贪心算法是算法设计中的一种方法。
• 期盼通过每个阶段的局部最优选择，从而达到全局的最优。
• 结果不一定最优。

2、应用场景

• 最少硬币找零问题
• 分数背包问题
• ……

3、场景剖析：零钱兑换

先用一张图来描述输入输出结果。

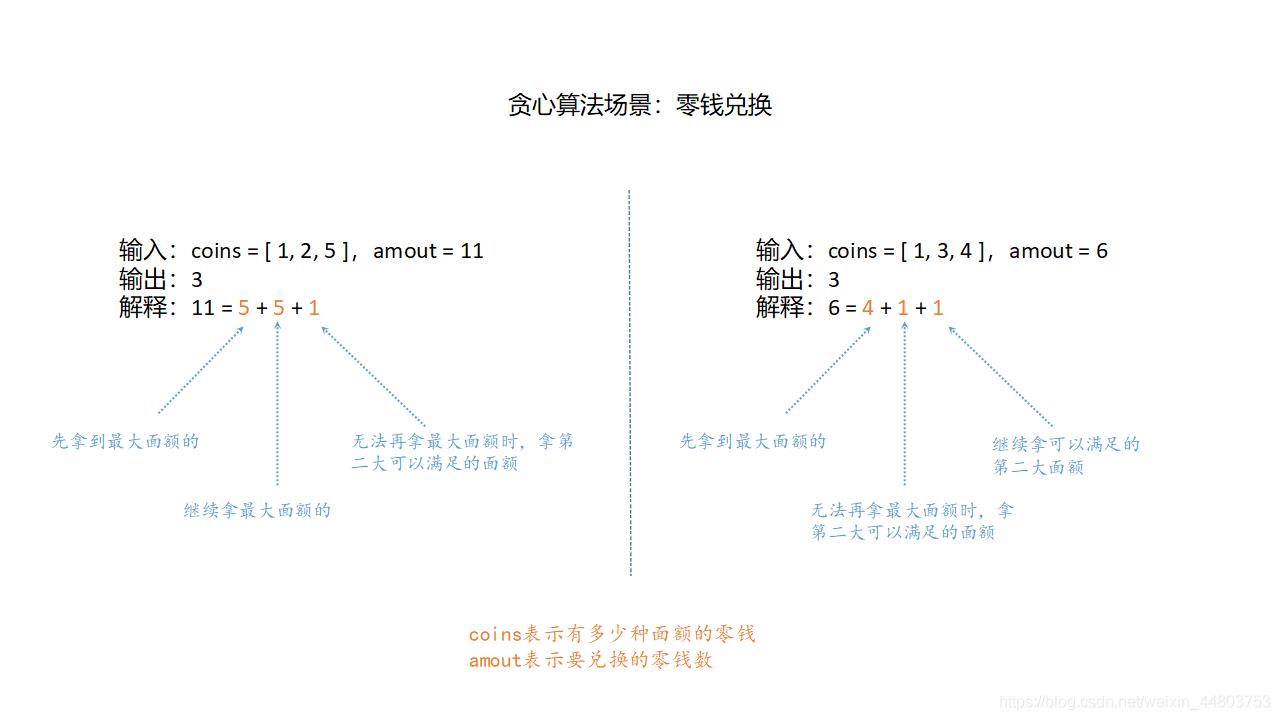
从上图中可以看到，如果用贪心算法解决零钱兑换问题的话，它会先从最大面额的硬币开始，拿尽可能多的这种硬币找零。当无法再拿更多这种价值的硬币时，开始拿第二大价值的硬币，依次继续。

大家可以发现，如果是第一种情况，确实可以达到理论最优。但是如果是第二种情况的话，还有一种更优的解法，那就是6 = 3 + 3。所以说，贪心算法并不总是能得到最优答案。

但是呢，虽说不能总是能得到最优答案，那我们为什么还有用它呢？

比起动态规则算法而言，贪心算法更简单、更快。虽然它并不总是能得到最优的答案，但是综合来看，它相对执行时间来说，输出了一个可以接受的解。

二、回溯算法

1、回溯算法是什么？

• 回溯算法是算法设计中的一种方法。
• 回溯算法是一种渐进式寻找并构建问题解决方式的策略。
• 回溯算法会先从一个可能的动作开始解决问题，如果不行，就回溯选择另一个动作，直到将问题解决。

2、什么问题适合选用回溯算法解决？

• 有很多路。
• 这些路里面，有死路，有活路。
• 通常需要递归来模拟所有的路。

2、应用场景

• 迷宫老鼠问题
• 数独解题器
• 骑士巡逻问题
• N皇后问题
• ……

3、场景剖析：全排列

先用一张图来战术输入输出的过程。

从上图中可以看到，全排列 [1, 2, 3] 三个元素，在递归的过程中会有很多种结果，比如说[1, 1, 2]，[1, 2, 1], [1, 2, 2]之类的结果。那么，当出现重复元素的时候，就会出现死路，这个时候就应该回退回去并去寻找下一条路活路走出去。这就是回溯算法要解决的问题。

三、贪心算法常见应用

引用leetcode的几道经典题目来强化贪心算法。

1、leetcode 455：分发饼干

（1）题意

这里附上原题链接

假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。

对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

输入输出示例：

• 输入: g = [1,2,3], s = [1,1]
• 输出: 1
• 解释:
  • 你有三个孩子和两块小饼干，3个孩子的胃口值分别是：1,2,3。
  • 虽然你有两块小饼干，由于他们的尺寸都是1，你只能让胃口值是1的孩子满足。
  • 所以你应该输出1。

（2）解题思路

• 既能满足孩子，还消耗最少。
• 先将“较小的饼干”分给“胃口较小”的孩子。

（3）解题步骤

• 对饼干数组和胃口数组升序降序。
• 遍历饼干数组，找到能满足第一个孩子的饼干。
• 然后继续遍历饼干数组，找到能满足第二、三、四、……、n个孩子的饼干。

（4）代码实现

/**
 * @param {number[]} g 孩子胃口
 * @param {number[]} s 饼干尺寸
 * @return {number}
 */
let findContentChildren = function(g, s) {

    // 实现升序排序
    const sortFunc = function(a, b){
        return a-b;
    }
    
    //对g进行升序排序，即从小到大排序
    g.sort(sortFunc);
    
    //对s进行升序排序，即从小到大排序
    s.sort(sortFunc);
    
    //定义初始值，记录饼干能满足多少个孩子
    let i = 0;
    
    //对排序后的饼干进行一一遍历，并逐一与孩子的胃口比对，如果能满足，则对i进行+1操作
    s.forEach(n => {
        if(n >= g[i]){
            i += 1;
        }
    });
    return i;
};

console.log(findContentChildren([1, 2], [1, 2, 3]));

2、leetcode 122：买卖股票的最佳时机

（1）题意

这里附上原题链接

给定一个数组 prices ，其中 prices[i] 是一支给定股票第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

输入输出示例：

• 输入: prices = [7,1,5,3,6,4]
• 输出: 7
• 解释:
  • 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
  • 随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。

（2）解题思路

• 前提：上帝视角，知道未来的价格。
• 局部最优：建好就收，见差就不动，不做长远打算。

（3）解题步骤

• 新建一个变量，用来统计总利润。
• 遍历价格数组，如果当前价格比昨天高，就是昨天买，今天卖，否则就不交易。
• 遍历结束后，返回所有利润之和。

（4）代码实现

/**
 * @param {number[]} prices
 * @return {number}
 */
let maxProfit = function(prices) {
    //新建一个变量，用来统计总利润
    let profit = 0;
    //遍历价格数组
    for(let i  = 1; i < prices.length; i++){
        //如果当前价格prices[i]比昨天prices[i - 1]高，就是昨天买，今天卖；
        //否则说明当前天数没买，不进行交易
        if(prices[i] > prices[i - 1]){
            //遍历过程中，不断对利润进行相加
            profit += prices[i] - prices[i-1];
        }
    }
    //遍历结束后，返回所有利润之和
    return profit;
};

console.log(maxProfit([7, 5, 4, 7]));

四、回溯算法常见应用

引用leetcode的几道经典题目来强化回溯算法。

1、leetcode 46：全排列

（1）题意

这里附上原题链接

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

输入输出示例：

• 输入: nums = [1,2,3]
• 输出: [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

（2）解题思路

• 要求：①所有排列情况；②没有重复元素。
• 有出路、有死路。
• 考虑回溯算法。

（3）解题步骤

• 用递归模拟出所有情况。
• 遇到包含重复元素的情况，就回溯。
• 收集所有到达递归终点的情况，并返回。

（4）代码实现

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
let permute = function(nums) {
    // 1.定义一个变量，收集所有结果的情况
    const res = [];
    const backtrack = (path) => {
        // 4.递归的重点收集所有满足题目要求的数组
        if(path.length === nums.length){
            res.push(path);
            return;
        }
        nums.forEach(n => {
            // 3.在把元素放进去时该数组已有此元素，那么此路为死路
            if(path.includes(n)){
                return;
            }
            backtrack(path.concat(n));
        });
    };
    // 2.递归时传入一个数组
    backtrack([]);
    return res;
};

console.log(permute([1, 2, 3]));

2、leetcode 78：子集

（1）题意

这里附上原题链接

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

输入输出示例：

• 输入: nums = [1,2,3]
• 输出: [[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

（2）解题思路

• 要求：①所有子集；②没有重复元素。
• 有出路、有死路。
• 考虑使用回溯算法。

（3）解题步骤

• 用递归模拟出所有情况。
• 保证接的数字都是后面的数字。
• 收集所有到达递归终点的情况，并返回。

（4）代码实现

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
 var subsets = function(nums) {
     //1.定义一个变量，存放结果
    const res = [];
    const backtrack = (path, l, start) => {
        // 4.到达路径终点时，push到结果里面
        if(path.length === l){
            res.push(path);
            return;
        }
        //3.不断遍历数组，并将其添加到path中
        for(let i = start; i < nums.length; i++){
            backtrack(path.concat(nums[i]), l, i + 1);
        }
    }
    //2.子集的长度有可能是0-nums.length不等
    for(let i = 0; i <= nums.length; i++){
        // 三个参数分别指：路径,路径数组的长度,起始的下标
        backtrack([], i, 0);
    }
    return res;
};

console.log(subsets([1, 2, 3]));

五、写在最后

贪心算法和回溯算法在前端的面试和笔试中也是非常经典的常考题。贪心算法相较于其他算法来说比较简单，而回溯算法涉及到很多溯回问题，逻辑较强，建议大家在做题目时如果看不懂的情况下可以选择多调试代码，一步一步跟着它的思路，多调试几遍，慢慢就能深入理解其逻辑了。

贪心算法和回溯算法在前端中的应用就讲到这里啦！如有不理解或文章有误欢迎评论区留言或私信我交流~

• 关注公众号 星期一研究室 ，第一时间关注技术干货，更多有趣的专栏待你解锁~
• 如果这篇文章对你有用，记得点个赞加个关注再走哦~
• 我们下期见！🥂🥂🥂