数据结构（部分）

Posted 可乐好哇！

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数据结构（部分）相关的知识，希望对你有一定的参考价值。

栈、队列、二叉树详解（小白专属）

栈（Stack）

  •    概念：是一种特殊的线性表，只允许在固定的一端进行插入和删除元素操作，另一端称为栈底。它遵守先进后出的原则。

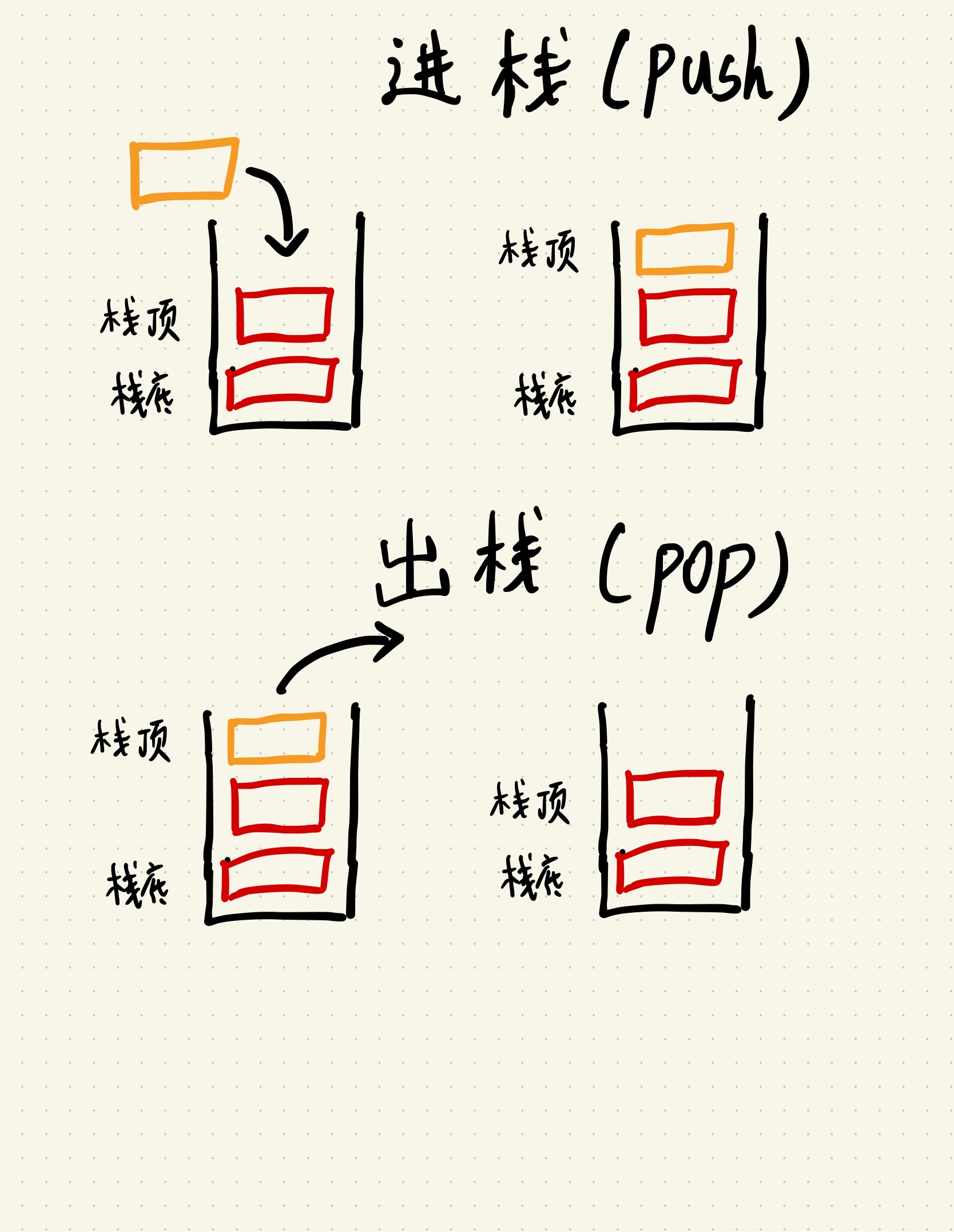
  • 代码实现：
    1.可以利用顺序表实现（使用尾插+尾删）稍微简单
    2. 可以利用链表实现（头尾都行）

public class MyStack {
   // 顺序表实现的栈
   public int[] elem = new int[100];
   public int usedSize = 0;

   public void push(int val) {
   		elem[usedSize] =  val;
   		usedSize++;
   }

   public int pop() {
   		return	elem[--usedSize];
   }

   public int peek() {
   		return	elem[usedSize - 1];
   }

   public boolean isEmpty() {
   	return usedSize == 0;
   }

   public int size() {
   	return usedSize;
   }
}

队列（Queue）

  •   概念：只允许在一端插入数据操作，在另一端进行删除操作的特殊线性表，队列遵循先进先出的原则。

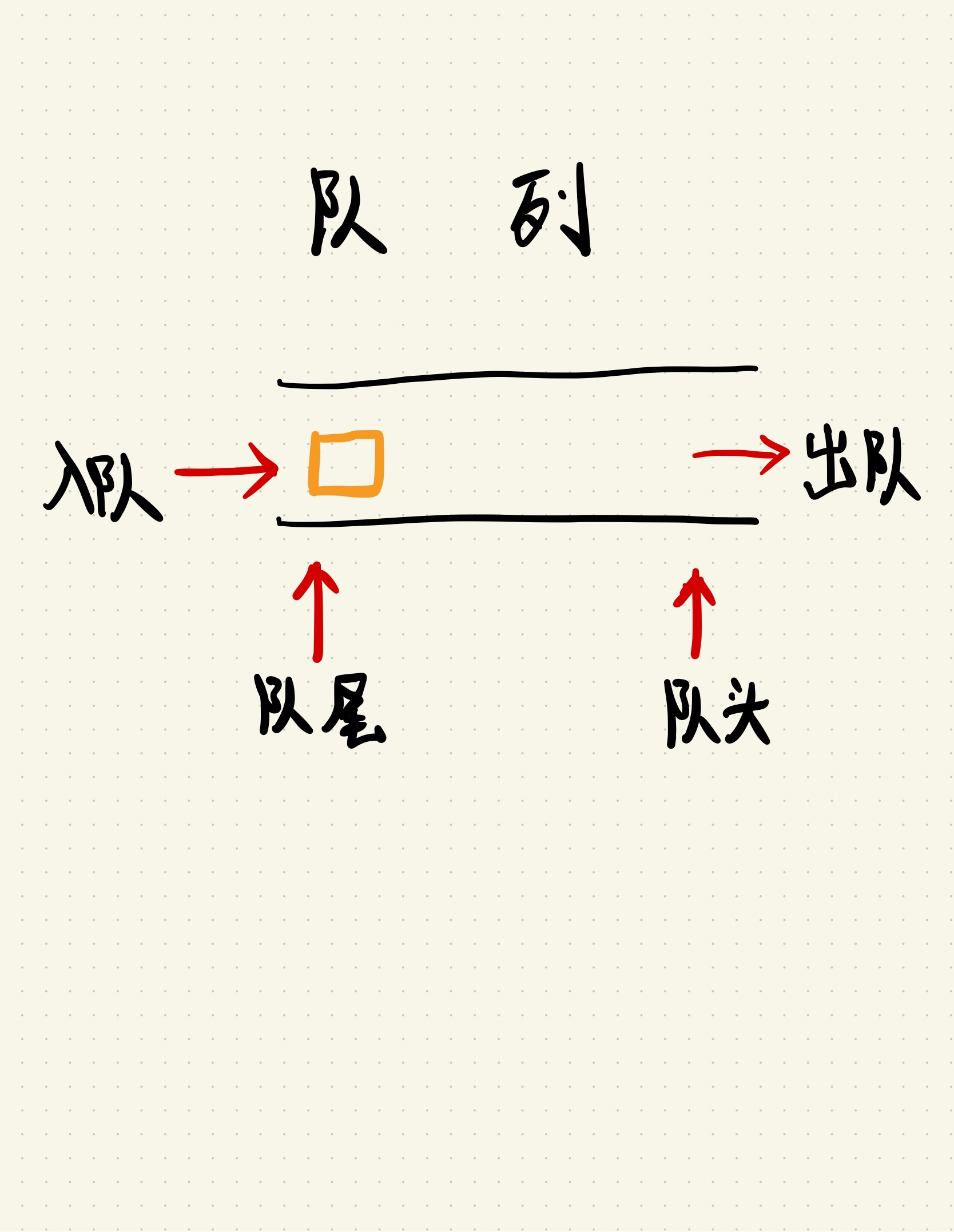
在这里插入图片描述
图解入队、出队过程：
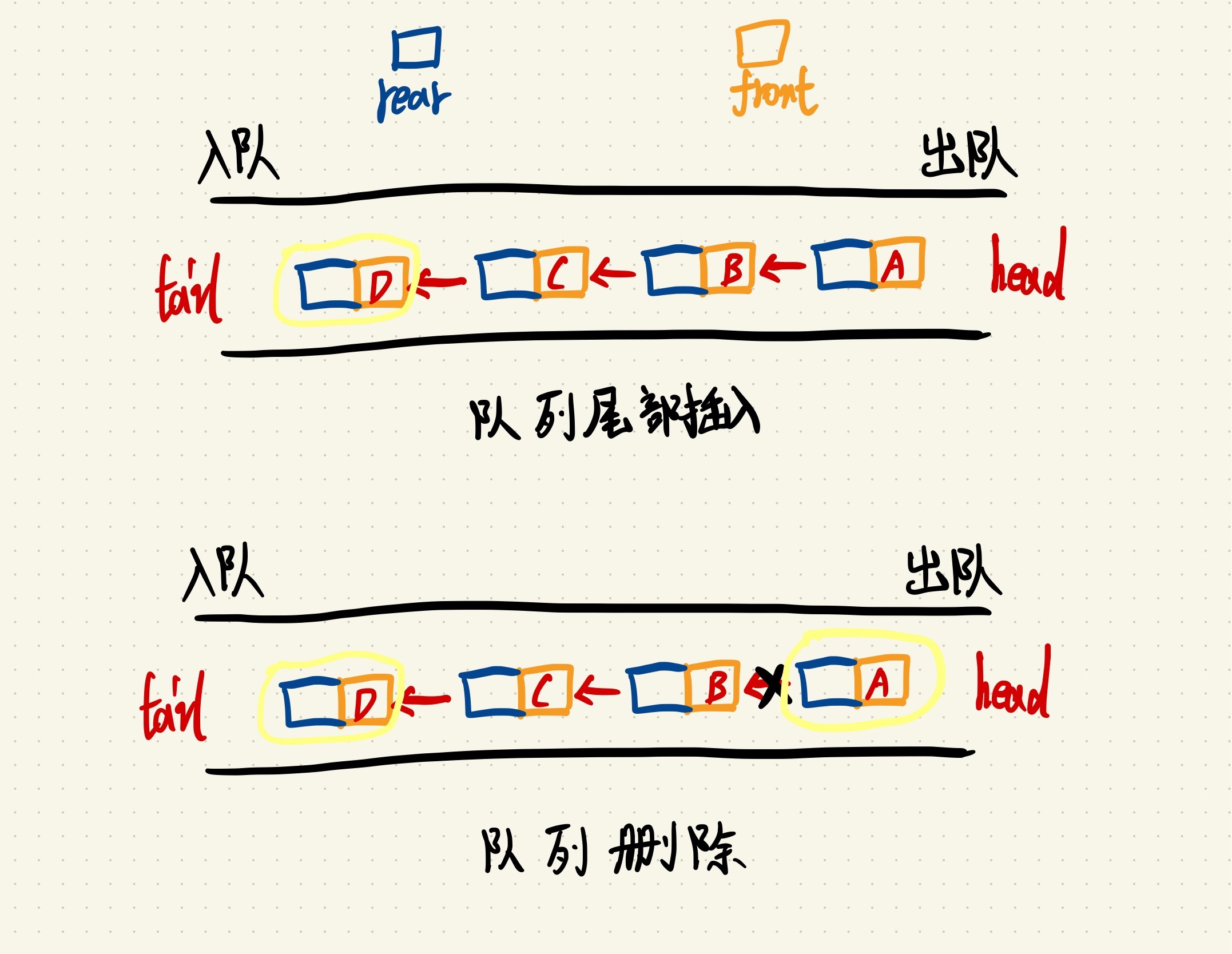
在这里插入图片描述

  • 代码实现：
      队列也可以用数组和链表的结构实现，推荐使用链表实现，相当于尾插法（效率会更高）
class Node {
    public int val;
    public Node next;

    public Node(int val) {
        this.val = val;
    }
}

public class MyQueue {

    public Node head = null;
    public Node tail = null;
    public int usedSize = 0;

    // 入队列（尾巴进）
    public void offer(int val) {
        Node node = new Node(val);
        if (this.tail == null) {
            this.head = node;
        } else {
            this.tail.next = node;
        }

        this.tail = node;
        this.usedSize++;
    }

    // 出队列（脑袋出）（删除头）
    public int poll() {
        if (this.usedSize == 0) {
            throw new RuntimeException("队列为空！");
        }

        Node oldHead = this.head;
        this.head = this.head.next;

        if (this.head == null) {
            this.tail = null;
        }

        this.usedSize--;
        return oldHead.val;
    }

    // 出队列(不删除)
    public int peek() {
        if (this.usedSize == 0) {
            throw new RuntimeException("队列为空！");
        }
        return this.head.val;
    }

    // 判断队列是否为空
    public boolean isEmpty() {
        return this.usedSize == 0;
    }

    // 使用的队列空间大小
    public int size() {
        return this.usedSize;
    }
}

二叉树

  • 概念：由一个根节点加上两颗别称左子树和右子树的二叉树组成。

  • 特点：

    1. 每个节点最多有两颗子树，二叉树不存在大于2的结点

    2. 二叉树的子树有左右之分，子树的次序不能颠倒，二叉树是有序树

  • 存储：

    1. 顺序存储

    2. 类似于链表的链式存储

    // 孩子表示法（推荐使用）
class Node {
		int val;				// 数据
		Node left;				// 左子树 
		Node right;				// 右子树
}

// 孩子双亲表示法
class Node {
		int val;				// 数据
		Node left;				// 左子树 
		Node right;				// 右子树
		Node parent;			// 当前结点的根结点 
}

  • 遍历图示：
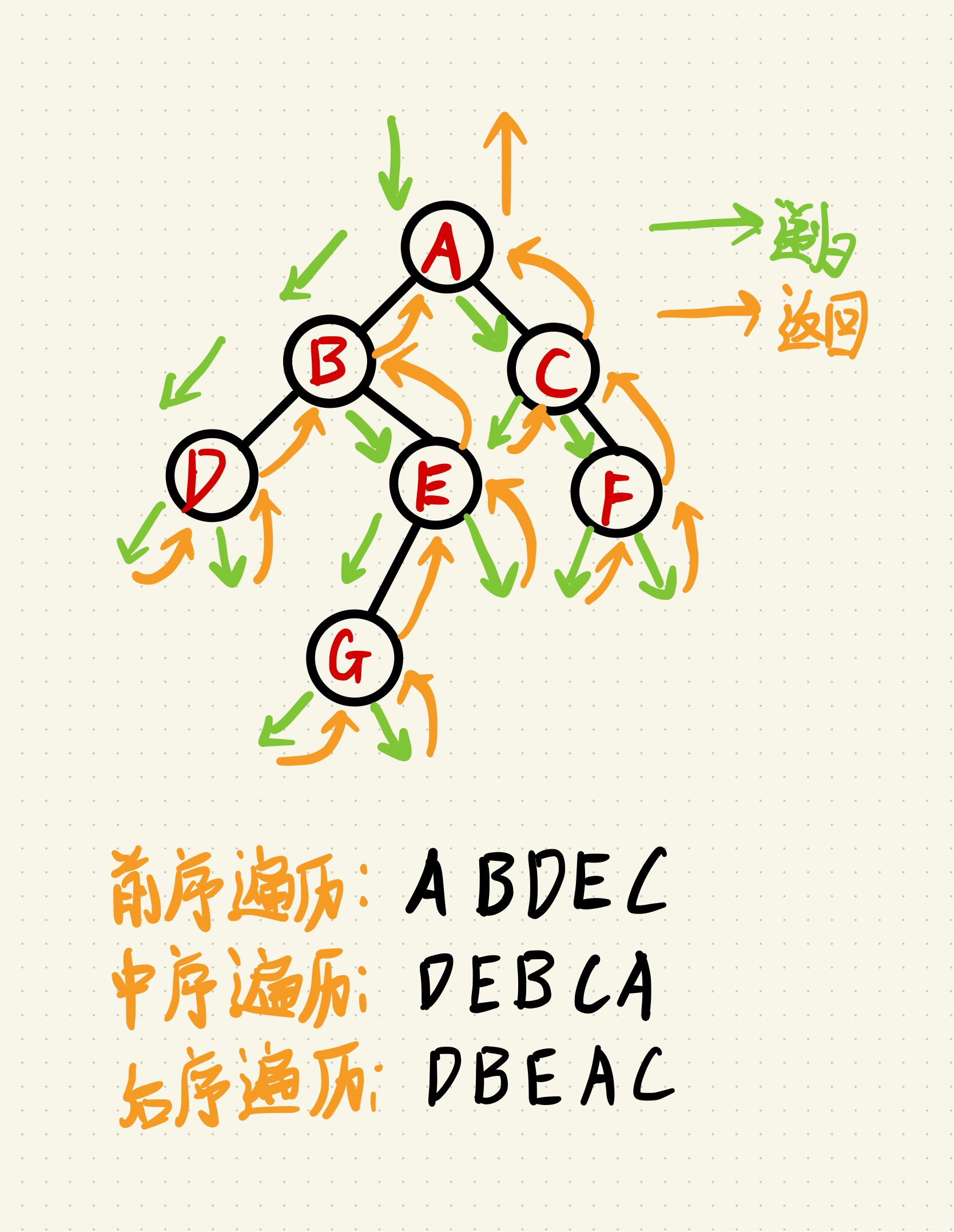
    在这里插入图片描述

  • 代码实现（递归）：

// 创建二叉树的结点
class TreeNode {

    int val;
    TreeNode left;
    TreeNode right;

    TreeNode() {
    }

    TreeNode(int val) {
        this.val = val;
    }

    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}
public class Solution() {
	// 前序遍历
    void preOrderTraversal(TreeNode root, List<Integer> res) {

        if (root == null) {
            return;
        }

        res.add(root.val);
        preOrderTraversal(root.left, res);
        preOrderTraversal(root.right, res);

    }

    // 中序遍历
    void inOrderTraversal(TreeNode root, List<Integer> res) {
        if (root == null) {
            return;
        }

        preOrderTraversal(root.left, res);
        res.add(root.val);
        preOrderTraversal(root.right, res);

    }

    // 后序遍历
    void postOrderTraversal(TreeNode root, List<Integer> res) {

        if (root == null) {
            return;
        }

        postOrderTraversal(root.left, res);
        postOrderTraversal(root.right, res);
        res.add(root.val);
    }

    // 子问题思路-求结点个数
    int getSize(TreeNode root) {
        if (root == null) {
            return 0;
        }

        return getSize(root.left) + getSize(root.right);
    }

    // 子问题思路-求叶子结点个数
    int getLeafSize(TreeNode root) {
        if (root == null) {
            return 0;
        }

        if (root.left == null && root.right == null) {
            return 1;
        }

        return getLeafSize(root.left) + getLeafSize(root.right);
    }

    // 子问题思路-求第 k 层结点个数
    int getKLevelSize(TreeNode root, int k) {
        if (root == null) {
            return 0;
        }

        if (k == 1) {
            return 1;
        }

        return getKLevelSize(root.left, k - 1) + getKLevelSize(root.right, k - 1);
    }

    // 获取二叉树的高度
    int getHeight(TreeNode root) {
        if (root == null) {
            return 0;
        }

        int l = getHeight(root.left);
        int r = getHeight(root.right);

        return l > r ? l + 1 : r + 1;
    }

    // 查找 val 所在结点，没有找到返回 null
    // 按照 根 -> 左子树 -> 右子树的顺序进行查找
    // 一旦找到，立即返回，不需要继续在其他位置查找
    TreeNode find(TreeNode root, int val) {
        if (root == null) {
            return null;
        }

        TreeNode l = find(root.left, val);
        if (l != null) {
            return l;
        }

        TreeNode r = find(root.right, val);
        if (r != null) {
            return r;
        }

        return null;
    }

    // 比较两个二叉树是否相同
    public boolean isSameTree(TreeNode p, TreeNode q) {

        if (p == null && q == null) {
            return true;
        }

        if (p == null && q != null || p != null && q == null) {
            return false;
        }

        if (p.val != q.val) {
            return false;
        }

        return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);

    }

    // 合并两个二叉树
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {

        // 如果root1为空 则使用root2的根
        if (root1 == null) {
            return root2;
        }
        // 同上
        if (root2 == null) {
            return root1;
        }

        // 都存在结点 就返回两个结点的和
        TreeNode node = new TreeNode(root1.val + root2.val);

        // 进行递归调用
        node.left = mergeTrees(root1.left, root2.left);
        node.right = mergeTrees(root1.right, root2.right);

        return node;
    }

}
  • 代码实现（非递归）：
 	//前序遍历
    public List<Integer> preorderTraversal(TreeNode root) {

        // 创建一个接收结果的ArrayList
        List<Integer> res = new ArrayList<>();

        if (root == null) {
            return res;
        }

        // 创建一个栈
        Stack<TreeNode> stack = new Stack<>();

        //定义一个node等于root
        TreeNode node = root;

        while (!stack.isEmpty() || node != null) {

            while (node != null) {
                res.add(node.val);
                stack.push(node);
                node = node.left;
            }

            node = stack.pop();
            node = node.right;

        }
        return res;
    }

    //中序遍历
    public List<Integer> inorderTraversal(TreeNode root) {

        List<Integer> res = new ArrayList<>();

        Stack<TreeNode> stack = new Stack<>();

        TreeNode node = root;

        while (node != null || !stack.isEmpty()) {

            while (node != null) {

                stack.push(node);
                node = node.left;

            }

            node = stack.pop();
            res.add(node.val);
            node = node.right;

        }
        return res;
    }

    //后序遍历
    public List<Integer> postorderTraversal(TreeNode root) {

        List<Integer> res = new ArrayList<>();

        Stack<TreeNode> stack = new Stack<>();

        if (root == null) {
            return res;
        }

        TreeNode node = root;
        TreeNode prevNode = null;

        while (node != null || !stack.isEmpty()) {

            while (node != null) {
                stack.push(node);
                node = node.left;
            }

            node = stack.pop();

            if (node.right == null || node.right == prevNode) {
                res.add(node.val);
                prevNode = node;
                node = null;
            } else {
                stack.push(node);
                node = node.right;
            }

        }
        return res;
    }

	// 层序遍历
	public void levelOrderTraversal(TreeNode root) {

        if (root == null) {
            return;
        }

        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);

        while (!queue.isEmpty()) {

            TreeNode cur = queue.poll();
            System.out.println(cur.val + " ");

            if (cur.left != null) {
                queue.offer(cur.left);
            }

            if (cur.right != null) {
                queue.offer(cur.right);
            }

        }

    }

补充

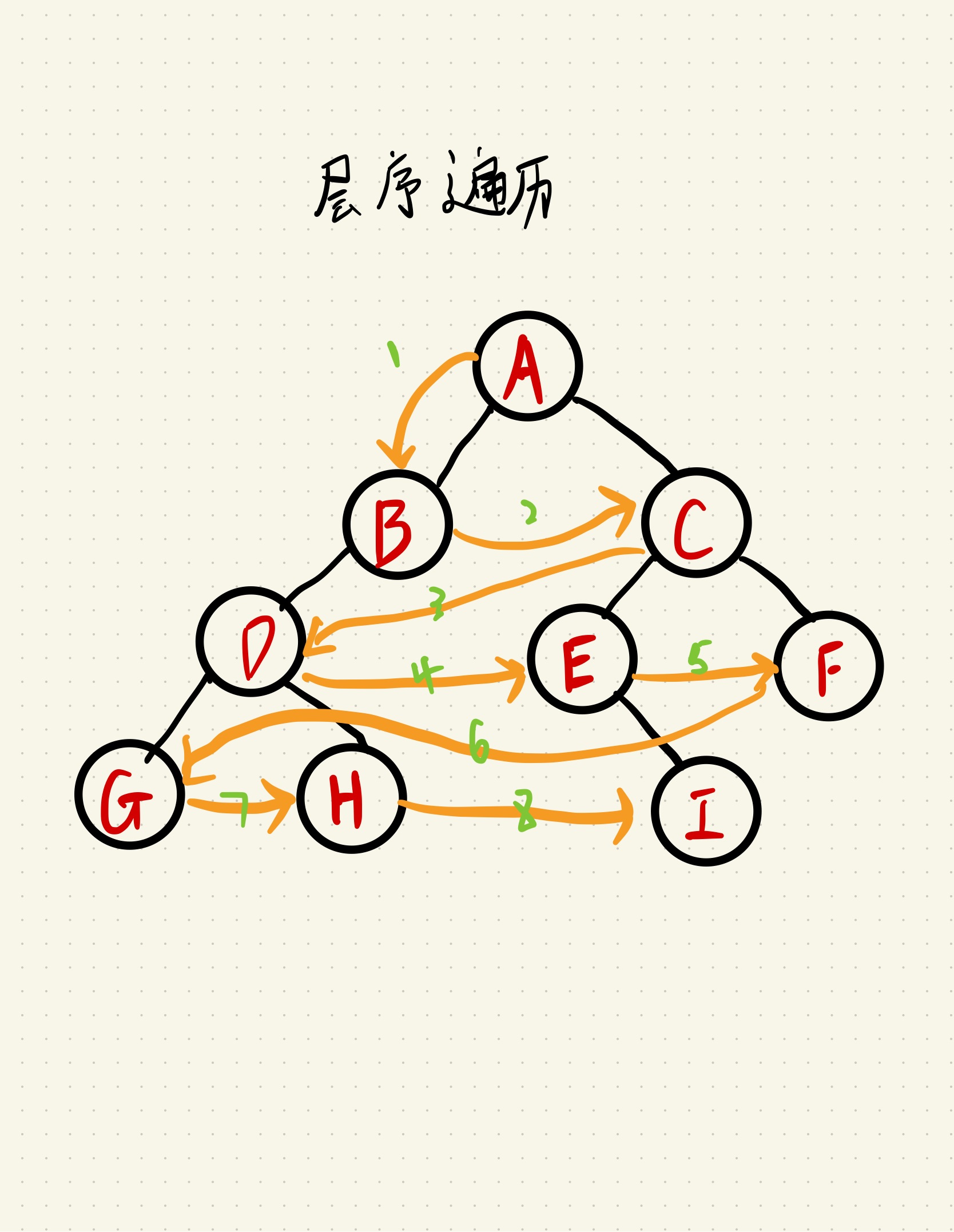
层序遍历（代码如上所述，过程图如下所示）:
         从所在二叉树的根结点出发，首先访问第一层的树根节点，然后从左到右访问第二层上的节点，接着依次往后推，自上而下，自左至右逐层访问数的节点的过程就是程序遍历。
在这里插入图片描述
不好之处请多多留言指点！！！

以上是关于数据结构（部分）的主要内容，如果未能解决你的问题，请参考以下文章

Wordpress - 将代码片段包含到布局的选定部分的插件

VS2015使用技巧 打开代码片段C#部分

;~ 小部分AutoHotkey源代码片段测试模板2019年10月9日.ahk

引用向量的部分片段？

如何在片段着色器中平铺部分纹理

AJAX相关JS代码片段和部分浏览器模型