快速傅里叶变化(FFT)含模板
Posted 皓洲
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了快速傅里叶变化(FFT)含模板相关的知识,希望对你有一定的参考价值。
快速傅里叶变化(FFT)
资料来源:https://www.bilibili.com/video/BV1Y7411W73U
前置知识索引
FFT的核心算法是基于复数和单位根的,并且在算法竞赛中FFT的最普遍应用是求i多项式乘法,或者是卷积。
复数 Complex Number
定
义
:
z
=
a
+
b
i
其
中
a
,
b
∈
R
,
i
=
n
加
法
法
则
:
(
a
+
b
i
)
+
(
c
+
d
i
)
=
(
a
+
c
)
+
(
b
+
d
)
i
乘
法
法
则
:
(
a
+
b
i
)
(
c
+
d
i
)
=
(
a
c
−
b
d
)
+
(
a
d
+
b
c
)
i
欧
拉
定
理
:
e
i
θ
=
cos
θ
+
i
sin
θ
定义:z = a + bi 其中 a,b∈R ,i =\\sqrt{n}\\\\ 加法法则:(a+bi)+(c+di) = (a+c)+(b+d)i\\\\ 乘法法则:(a+bi)(c+di) = (ac-bd)+(ad+bc)i\\\\ 欧拉定理:{e}^{iθ} = \\cosθ+i\\sinθ
定义:z=a+bi其中a,b∈R,i=n加法法则:(a+bi)+(c+di)=(a+c)+(b+d)i乘法法则:(a+bi)(c+di)=(ac−bd)+(ad+bc)i欧拉定理:eiθ=cosθ+isinθ
复数的几何意义
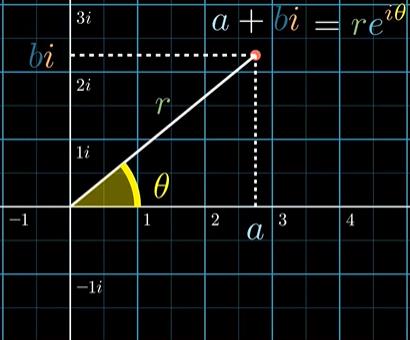
单位根
快速傅里叶变换的核心是用单位根的某些独特性质来快速实现的
我们知道每个复数都可以表示为:
z
=
r
∗
e
i
θ
z = r*{e}^{iθ}\\\\
z=r∗eiθ
所以两复数相乘可以表示为
z
2
=
r
2
∗
e
(
2
θ
)
i
z^2 = r^2*e^{(2θ)i}
z2=r2∗e(2θ)i
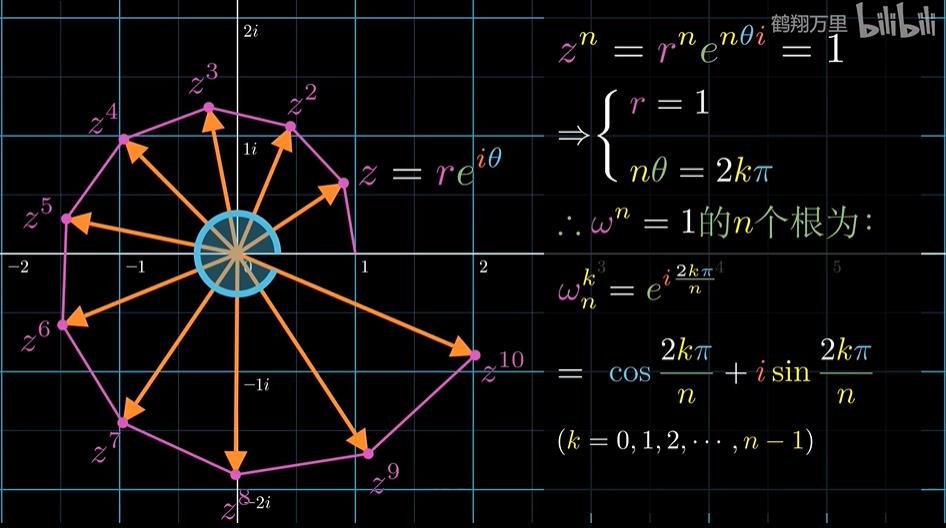
每个单位根都可以看成如下公式单位根的幂
ω
n
=
e
i
2
π
n
ω_n = e^{i{\\frac{2\\pi}{n}}}
ωn=ein2π
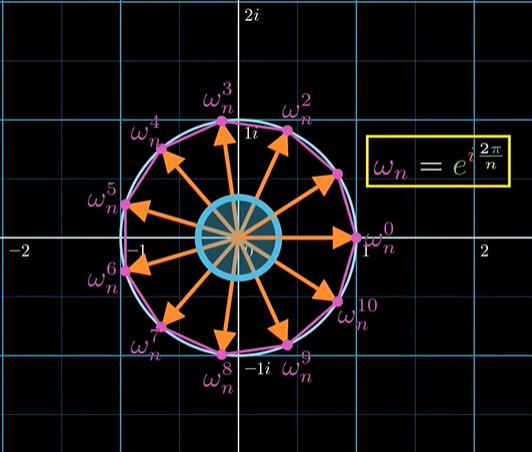
单位根-三个引理
- lemma.1 消去引理:
ω d k d n = ω k n ω n n 2 = ω 2 = − 1 ω_{dk}^{dn} = ω_{k}^{n}\\\\ ω^{\\frac{n}{2}}_{n} = ω_{2} = -1\\\\ ωdkdn=ωknωn2n=ω2=−1
证明:
ω
d
k
d
n
=
(
e
2
π
d
n
i
)
d
k
=
(
e
2
π
n
i
)
k
=
ω
k
n
ω_{dk}^{dn}=(e^{\\frac{2\\pi}{dn}i})^{dk} = (e^{\\frac{2\\pi}{n}i})^{k} = ω_{k}^{n}
ωdkdn=(edn2πi)dk=(en2πi)k=ωkn
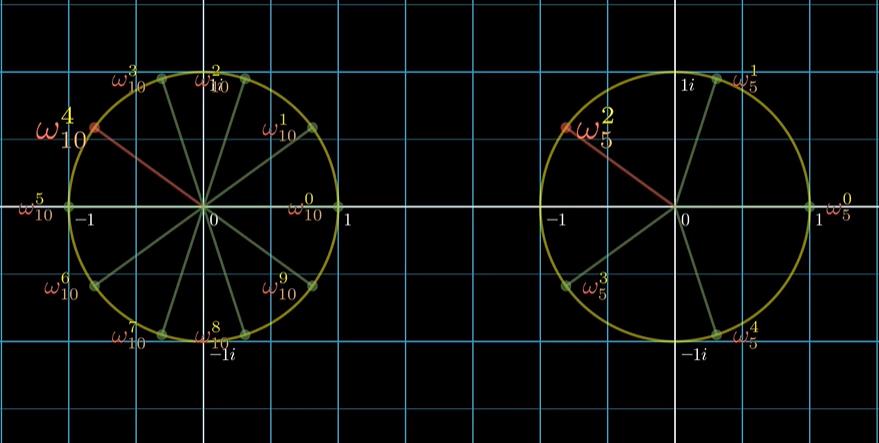
- lemma.2 折半引理:
( ω n k + n 2 ) 2 = ( ω k n ) 2 = ω n 2 k (ω^{k+\\frac{n}{2}}_{n})^2 = (ω_{k}^{n})^2 = ω_{\\frac{n}{2}}^{k}\\\\ (ωnk+2n)2=(ωkn)2=ω2nk
证明:
ω
n
k
+
n
2
=
ω
n
k
ω
n
n
2
=
−
ω
n
k
(
ω
n
k
)
2
=
ω
n
2
k
=
ω
n
2
k
ω
n
k
+
n
2
=
ω
n
k
ω
n
n
2
=
−
ω
n
k
(
ω
n
k
)
2
=
ω
n
2
k
=
ω
n
2
k
ω^{k+\\frac{n}{2}}_{n} = ω_{n}^{k}ω_{n}^{\\frac{n}{2}} =- ω_{n}^{k}\\\\ (ω^{k}_{n})^2 = ω_{n}^{2k} = ω_{\\frac{n}{2}}^{k}\\\\ω^{k+\\frac{n}{2}}_{n} = ω_{n}^{k}ω_{n}^{\\frac{n}{2}} =- ω_{n}^{k}\\\\ (ω^{k}_{n})^2 = ω_{n}^{2k} = ω_{\\frac{n}{2}}^{k}\\\\
ωnk+2n=ωnkωn2n=−ωnk(ωnk)2=ωn2k=ω2nkωnk+2n=ωnk以上是关于快速傅里叶变化(FFT)含模板的主要内容,如果未能解决你的问题,请参考以下文章