强网杯2021 ctf线上赛ezmath wp(#超详细,带逆向新手走过一个又一个小坑)
Posted 漫小牛
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了强网杯2021 ctf线上赛ezmath wp(#超详细,带逆向新手走过一个又一个小坑)相关的知识,希望对你有一定的参考价值。
文章目录
引言
这是强网杯2021中的一道Reverse题,题目是ezmath,将附件进行下载,名称为chall,说明这道题跟数学有关,都说ctf比赛三大谎言:ez、eazy和baby,名称简单,实则并不简单。做出这道题,需要的数学知识远远大于逆向知识。
题目附件:
链接:https://pan.baidu.com/s/13TheaHB7XcbGnBp-M1N5Rg
提取码:k4pm
一、分析文件类型
使用Exeinfo PE查看文件的类型,该工具主要用来查看文件是否为可执行文件,是否为动态链接库,是否有壳以及运行的操作系统等等。具体情况见下图:
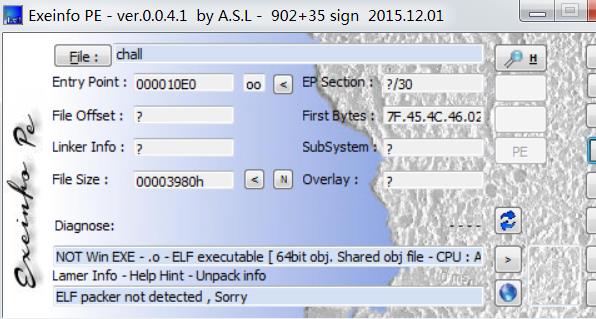
从图中可知,该程序是64位的elf文件,无壳。
二、初步分析
1 运行情况
运行一下程序,需要输入一串字符,由于是随便输入的,结果为wrong,想必输入的字符就是flag。
2 IDA初步分析
拖入IDA中,shift+f12常规操作查找关键字符串:
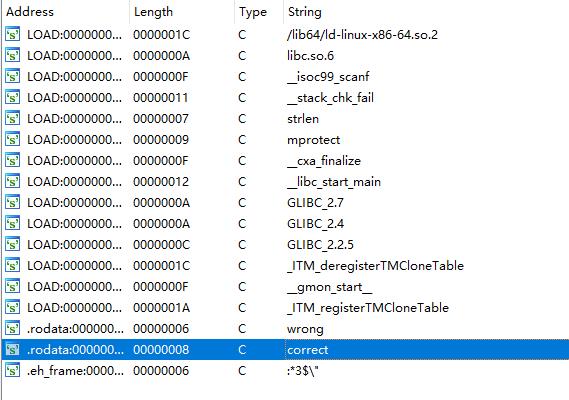
从correct字符的输出位置即可定位到代码段:
__int64 __fastcall main(int a1, char **a2, char **a3)
{
__int64 result; // rax
int i; // [rsp+Ch] [rbp-44h]
char s[8]; // [rsp+20h] [rbp-30h] BYREF
__int64 v6; // [rsp+28h] [rbp-28h]
__int64 v7; // [rsp+30h] [rbp-20h]
__int64 v8; // [rsp+38h] [rbp-18h]
__int64 v9; // [rsp+40h] [rbp-10h]
unsigned __int64 v10; // [rsp+48h] [rbp-8h]
v10 = __readfsqword(0x28u);
*(_QWORD *)s = 0LL;
v6 = 0LL;
v7 = 0LL;
v8 = 0LL;
v9 = 0LL;
__isoc99_scanf("%39s");
if ( strlen(s) == 38 )
{
for ( i = 0; i <= 37; i += 2 )
{
if ( dbl_4020[i / 2] != sub_13F3(*(unsigned __int16 *)&s[i]) )
goto LABEL_2;
}
puts("correct");
result = 0LL;
}
else
{
LABEL_2:
puts("wrong");
result = 0LL;
}
return result;
}
看到main函数,说明代码并不太复杂,简单看一下,有如下一些初步的结果:
- 输入字符的长度为38
- 关键函数为sub_13F3,将函数的返回值和dbl_4020比较时必须相等
- 关键函数sub_13F3的参数是2个bytes,也就是每次从输入的38个字符中取两个
提取出dbl_4020的数据为:
double dbl_4020[19] =
{
0.00009794904266317233,
0.00010270456917442,
0.00009194256152777895,
0.0001090322021913372,
0.0001112636336217534,
0.0001007442677411854,
0.0001112636336217534,
0.0001047063607908828,
0.0001112818534005219,
0.0001046861985862495,
0.0001112818534005219,
0.000108992856167966,
0.0001112636336217534,
0.0001090234561758122,
0.0001113183108652088,
0.0001006882924839248,
0.0001112590796092291,
0.0001089841164633298,
0.00008468431512187874
};
三、详细分析
1 sub_13F3函数分析
既然sub_13F3函数是关键函数,就先来分析它:
double __fastcall sub_13F3(int a1)
{
int i; // [rsp+8h] [rbp-Ch]
double v3; // [rsp+Ch] [rbp-8h]
v3 = unk_2010;
for ( i = 8225; i < a1; ++i )
v3 = 2.718281828459045 - (double)i * v3;
return v3;
}
这个函数关键代码只有3行,v3的初始值是0.2021,a1是输入的两个字符转化为的unsigned short型整数,不要看这里的参数int a,要看调用位置的强制类型转换:
if ( dbl_4020[i / 2] != sub_13F3(*(unsigned __int16 *)&s[i]) )
goto LABEL_2;
循环中,迭代从8225加到a1,将结果保存到v3中返回,既然如此,就可以按这个程序写逻辑,每两个字符跑一下这个函数,然后跟dbl_4020[19]里的19个数依次比较,最后把38个数算出来,真的这么简单吗?就写出exp跑跑看吧:
#include <stdio.h>
#include <string.h>
double dbl_4020[19] =
{
0.00009794904266317233,
0.00010270456917442,
0.00009194256152777895,
0.0001090322021913372,
0.0001112636336217534,
0.0001007442677411854,
0.0001112636336217534,
0.0001047063607908828,
0.0001112818534005219,
0.0001046861985862495,
0.0001112818534005219,
0.000108992856167966,
0.0001112636336217534,
0.0001090234561758122,
0.0001113183108652088,
0.0001006882924839248,
0.0001112590796092291,
0.0001089841164633298,
0.00008468431512187874
};
main()
{
long long a = 0x3FC9DE69AD42C3CA;
printf("size of a is %d\\n",sizeof(a));
double d = *(double *)&a;
printf("%f\\n", d);
int i = 0;
int j = 0;
int k = 0;
double result = 0;
printf("1st is %lf\\n", dbl_4020[j]);
// for(i = 0; i<18; i++)
// {
result = d;
for(k = 8225; k<9000; k++)
{
result = (double)2.718281828459045 - (double)k * result;
printf("k is %d; result is %f\\n", k, result);
//break;
if(dbl_4020[j]>result)
{
//printf("%d\\n", k);
}
}
// }
}
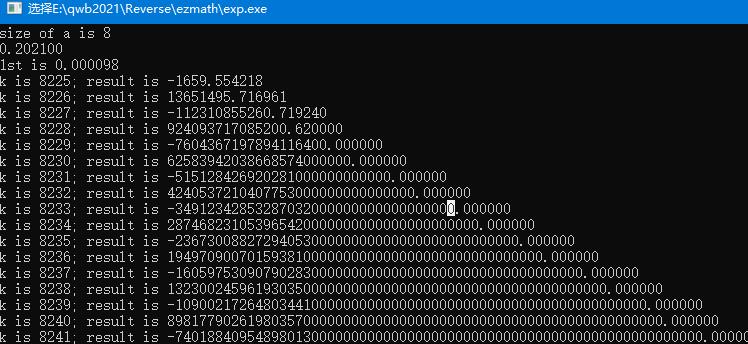
从运行结果看,这个值越来越发散,跑到8303就开始越界了:
2 查找蛛丝马迹
(1)mprotect
既然这道题没这么简单,那么就老老实实的分析程序逻辑吧,在IDA的funciton窗口,可以找到mprotect这个函数,这是这道题的第一个小坑,它的功能是修改某一块儿内存区域的是否可读、是否可写、是否可执行的状态的,它的调用位置是在sub_1391函数中:
__int64 sub_1391()
{
__int64 result; // rax
mprotect((void *)((unsigned __int64)(&qword_2018 - 1) & 0xFFFFFFFFFFFFF000LL), 0x1000uLL, 7);
((void (__fastcall *)(double (__fastcall *)(double), double, double))((char *)&sub_11C8 + 1))(sub_1301, 0.0, 1.0);
result = 0LL;
*(&qword_2018 - 1) = 0LL;
return result;
}
从这个函数中,也可以看到mprotect函数把(unsigned __int64)(&qword_2018 - 1) & 0xFFFFFFFFFFFFF000LL)的位置设置成了7,可读可写可执行,由于设置过程是按页的,所以要&一个0xFFFFFFFFFFFFF000LL,虽然mprotect没有直接写unk_2010的位置,但通过&qword_2018 - 1实际指向的也是这个位置,现在的关键就是看看这个值修改成了什么。
(2)重写unk_2010
在这个函数return前,执行了*(&qword_2018 - 1) = 0LL,这条语句就是对unk_2010的写入操作,也是逆向新手可能遇到的第二个坑,那么这个值真的写的是0吗?如果拿0作为sub_13F3中v3的初始值计算,显然跑不出结果。
这里的解决思路是:不要相信IDA的伪代码,有问题的时候要看汇编。
下面来解决这个小坑,首先给出sub_1391函数的汇编代码:
.text:0000000000001391 sub_1391 proc near ; CODE XREF: init+49↓p
.text:0000000000001391 ; DATA XREF: .init_array:0000000000003D88↓o
.text:0000000000001391
.text:0000000000001391 var_8 = qword ptr -8
.text:0000000000001391
.text:0000000000001391 ; __unwind {
.text:0000000000001391 endbr64
.text:0000000000001395 push rbp
.text:0000000000001396 mov rbp, rsp
.text:0000000000001399 sub rsp, 10h
.text:000000000000139D lea rax, qword_2018
.text:00000000000013A4 sub rax, 8
.text:00000000000013A8 mov [rbp+var_8], rax
.text:00000000000013AC mov rax, [rbp+var_8]
.text:00000000000013B0 and rax, 0FFFFFFFFFFFFF000h
.text:00000000000013B6 mov edx, 7 ; prot
.text:00000000000013BB mov esi, 1000h ; len
.text:00000000000013C0 mov rdi, rax ; addr
.text:00000000000013C3 call _mprotect
.text:00000000000013C8 movsd xmm0, cs:qword_2050
.text:00000000000013D0 movapd xmm1, xmm0
.text:00000000000013D4 pxor xmm0, xmm0
.text:00000000000013D8 lea rdi, sub_1301
.text:00000000000013DF call near ptr sub_11C8+1
.text:00000000000013E4 movq rax, xmm0
.text:00000000000013E9 mov rdx, [rbp+var_8]
.text:00000000000013ED mov [rdx], rax
.text:00000000000013F0 nop
.text:00000000000013F1 leave
.text:00000000000013F2 retn
.text:00000000000013F2 ; } // starts at 1391
从汇编可以看出,.text:00000000000013ED的位置写入修改后的unk_2010的代码,这个值是rax,这个值又是从xmm0获得的,xmm0是0吗?由于IDA对向量寄存器的反编译支持的不太好(至少免费版是这样),在伪代码中没有变量直接表示xmm0寄存器(在这个例子中大部分是通过double型的变量来表示的),因此IDA错误的解析为0。解析为0的另一个原因是在mprotect和*(&qword_2018 - 1) = 0LL;中间进行了函数调用:
((void (__fastcall *)(double (__fastcall *)(double), double, double))((char *)&sub_11C8 + 1))(sub_1301, 0.0, 1.0);
如果跟到这一行代码里认真分析,就能慢慢的找到xmm0是这个调用的返回值,也是要重写0.2021的关键代码(具体过程当然也是看汇编,跟上面的方法一样,这里先略过)。
3 分析重写unk_2010的值(一)
分析重写unk_2020是这道题最复杂的部分,也需要坚实的理论基础,关键部分还是下面的这行代码,由于比较重要,再打出来一遍:
((void (__fastcall *)(double (__fastcall *)(double), double, double))((char *)&sub_11C8 + 1))(sub_1301, 0.0, 1.0);
这个函数是(char *)&sub_11C8 + 1),有三个参数,第一个参数是一个函数指针,指向sub_1301,第二个参数是0.0,第三个参数是1.0。首先来看sub_11C8:
void __fastcall sub_11C8(double (__fastcall *a1)(double), double a2, double a3)
{
int i; // [rsp-28h] [rbp-30h]
double v5; // [rsp-20h] [rbp-28h]
double v6; // [rsp-18h] [rbp-20h]
double v7; // [rsp-10h] [rbp-18h]
v7 = (a3 - a2) / (double)1000;
v5 = a1(v7 / 2.0 + a2);
v6 = 0.0;
for ( i = 1; i < 1000; ++i )
{
v5 = a1(v7 / 2.0 + (double)i * v7 + a2) + v5;
v6 = a1((double)i * v7 + a2) + v6;
}
a1(a2);
a1(a3);
}
这个函数执行了一些操作,操作中多次调用a1,即sub_1301:
double __fastcall sub_1301(double a1)
{
int i; // [rsp+Ch] [rbp-1Ch]
double v3; // [rsp+10h] [rbp-18h]
double v4; // [rsp+18h] [rbp-10h]
double v5; // [rsp+20h] [rbp-8h]
v3 = 1.0;
v4 = 1.0;
v5 = 1.0;
for ( i = 1; i <= 8225; ++i )
{
v3 = v3 * a1;
v5 = (double)i * v5;
v4 = v3 / v5 + v4;
}
return v3 * v4;
}
相比sub_11C8,还是这个函数好理解一些,逐行分析代码可知,该函数计算出的结果为:
x
8225
∗
(
1
+
x
1
1
!
+
x
2
2
!
+
x
3
3
!
+
.
.
.
+
x
8225
8225
!
)
{x^{8225}}*(1 + \\frac{{{x^1}}}{{1!}} + \\frac{{{x^2}}}{{2!}} + \\frac{{{x^3}}}{{3!}} + ... + \\frac{{{x^{8225}}}}{{8225!}})
x8225∗(1+1!x1+2!x2+3!x3+...+8225!x8225)
看到这个就要往高等数学级数这一章去想,看看到底是个啥?原来后面那一堆阶乘和是
e
x
{e^x}
ex的泰勒展开式。这个函数搞清楚后,是不是就先放在这里呢?吸取了之前的经验,再去看看汇编,为了节省篇幅,只列出sub_1301汇编的最后几行:
.text:000000000000137C cmp [rbp+var_1C], 2021h
.text:0000000000001383 jle short loc_133E
.text:0000000000001385 movsd xmm0, [rbp+var_18]
.text:000000000000138A mulsd xmm0, [rbp+var_10]
.text:000000000000138F pop rbp
.text:0000000000001390 retn
.text:0000000000001390 ; } // starts at 1301
从这几行可知,返回值就是xmm0,下面,可以放心的回到sub_11C8来看了。
从上往下看,一切都很正常,但到了最后两行代码就有些奇怪,a1(a2);和a1(a3);a1是函数sub_1301,a3是参数传入的1.0,好像这些计算和上面那一堆操作没有关系啊?除了最后一行,上面的一堆都是废代码吗?CTF比赛中,当然有这个可能,用来干扰视听。但为了保险起见,还是去看汇编(又是看汇编,大家的IDA也是这样吗?有点儿怀疑了)。那就贴出来分析吧:
.text:00000000000011C8 sub_11C8 proc near ; CODE XREF: sub_1391+4E↓p
.text:00000000000011C8 push rbx
.text:00000000000011CA
.text:00000000000011CA loc_11CA:
.text:00000000000011CA nop edx
.text:00000000000011CD push rbp
.text:00000000000011CE mov rbp, rsp
.text:00000000000011D1 sub rsp, 40h
.text:00000000000011D5 mov [rbp-28h], rdi
.text:00000000000011D9 movsd qword ptr [rbp-30h], xmm0
.text:00000000000011DE movsd qword ptr [rbp-38h], xmm1
.text:00000000000011E3 mov dword ptr [rbp-1Ch], 3E8h
.text:00000000000011EA movsd xmm0, qword ptr [rbp-38h]
.text:00000000000011EF subsd xmm0, qword ptr [rbp-30h]
.text:00000000000011F4 cvtsi2sd xmm1, dword ptr [rbp-1Ch]
.text:00000000000011F9 divsd xmm0, xmm1
.text:00000000000011FD movsd qword ptr [rbp-8], xmm0
.text:0000000000001202 movsd xmm0, qword ptr [rbp-8]
.text:0000000000001207 movsd xmm1, cs:qword_2038
.text:000000000000120F divsd xmm0, xmm1
.text:0000000000001213 addsd xmm0, qword ptr [rbp-30h]
.text:0000000000001218 mov rax, [rbp-28h]
.text:000000000000121C call rax
.text:000000000000121E movq rax, xmm0
.text:0000000000001223 mov [rbp-18h], rax
.text:0000000000001227 pxor xmm0, xmm0
.text:000000000000122B movsd qword ptr [rbp-10h], xmm0
.text:0000000000001230 mov dword ptr [rbp-20h], 1
.text:0000000000001237 jmp short loc_129C
.text:0000000000001239 ; ---------------------------------------------------------------------------
.text:0000000000001239
.text:0000000000001239 loc_1239: ; CODE XREF: sub_11C8+DA↓j
.text:0000000000001239 cvtsi2sd xmm0, dword ptr [rbp-20h]
.text:000000000000123E mulsd xmm0, qword ptr [rbp-8]
.text:0000000000001243 movapd xmm1, xmm0
.text:0000000000001247 addsd xmm1, qword ptr [rbp-30h]
.text:000000000000124C movsd xmm0, qword ptr [rbp-8]
.text:0000000000001251 movsd xmm2, cs:qword_2038
.text:0000000000001259 divsd xmm0, xmm2
.text:000000000000125D addsd xmm0, xmm1
.text:0000000000001261 mov rax, [rbp-28h]
.text:0000000000001265 call rax
.text:0000000000001267 movsd xmm1, qword ptr [rbp-18h]
.text:000000000000126C addsd xmm0, xmm1
.text:0000000000001270 movsd qword ptr [rbp-18h], xmm0
.text:0000000000001275 cvtsi2sd xmm0, dword ptr [rbp-20h]
.text:000000000000127A mulsd xmm0, qword ptr [rbp-8]
.text:000000000000127F addsd xmm0, qword ptr [rbp-30h]
.text:0000000000001284 mov rax, [rbp-28h]
.text:0000000000001288 call rax
.text:000000000000128A movsd xmm1, qword ptr [rbp-10h]
.text:000000000000128F addsd xmm0, xmm1
.text:0000000000001293 movsd qword ptr [rbp-10h], xmm0
.text:0000000000001298 add dword ptr [rbp-20h], 1
.text:000000000000129C
.text:000000000000129C loc_129C: ; CODE XREF: sub_11C8+6F↑j
.text:000000000000129C mov eax, [rbp-20h]
.text:000000000000129F cmp eax, [rbp-1Ch]
.text:00000000000012A2 jl short loc_1239
.text:00000000000012A4 mov rax, [rbp-30h]
.text:00000000000012A8 mov rdx, [rbp-28h]
.text:00000000000012AC movq xmm0, rax
.text:00000000000012B1 call rdx
.text:00000000000012B3 movsd xmm2, qword ptr [rbp-18h]
.text:00000000000012B8 movsd xmm1, cs:qword_2040
.text:00000000000012C0 mulsd xmm1, xmm2
.text:00000000000012C4 addsd xmm1, xmm0
.text:00000000000012C8 movsd xmm0, qword ptr [rbp-10h]
.text:00000000000012CD addsd xmm0, xmm0
.text:00000000000012D1 addsd xmm1, xmm0
.text:00000000000012D5 movsd qword ptr [rbp-40h], xmm1
.text:00000000000012DA mov rax, [rbp-38h]
.text:00000000000012DE mov rdx, [rbp-28h]
.text:00000000000012E2 movq xmm0, rax
.text:00000000000012E7 call rdx
.text:00000000000012E9 addsd xmm0, qword ptr [rbp-40h]
.text:00000000000012EE mulsd xmm0, qword ptr [rbp-8]
.text:00000000000012F3 movsd xmm1, cs:qword_2048
.text:00000000000012FB divsd xmm0, xmm1
.text:00000000000012FF leave
.text:0000000000001300 retn
.text:0000000000001300 ; } // starts at 11C9
为了保险起见,从头到尾对照汇编和伪代码读一遍,直到最后两行就会发现问题,从.text:00000000000012A4到.text:00000000000012B1对应伪代码a1(a2);进行修正,分析的技巧是,一定要自己把堆栈画出来。一直到.text:00000000000012D1,可以解析出代码:
v4 = v54+a1(a2)+2v6,v4放在rbp-40h的位置。
从.text:00000000000012DA到.text:00000000000012E7对应伪代码a1(a3),接着解析,可以解析出代妈xmm0 = (a1(a3)+v4)*v7/6.0,到这里,就分析完了。
虽然解析出来了,但这个到底是个啥?这是逆向新手可能遇到的第三个坑,即识别sub_11C8的功能。这个计算实际上是辛普森积分,公式如下:
∫
a
b
f
(
x
)
d
x
≈
b
−
a
6
n
[
y
0
+
y
2
n
+
4
(
y
1
+
y
3
+
.
.
.
+
y
2
n
−
1
)
+
2
(
y
2
+
y
4
+
.
.
.
+
y
2
n
−
2
)
]
\\int_a^b {f(x)dx \\approx \\frac{{b - a}}{{6n}}[{y_0} + {y_{2n}} + 4({y_1} + {y_3} + ... + {y_{2n - 1}}) + 2({y_2} + {y_4} + ... + {y_{2n - 2}})]}
∫abf(x)dx≈6nb−a[y0以上是关于强网杯2021 ctf线上赛ezmath wp(#超详细,带逆向新手走过一个又一个小坑)的主要内容,如果未能解决你的问题,请参考以下文章