凸优化中的对偶问题
Posted LeoJarvis
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了凸优化中的对偶问题相关的知识,希望对你有一定的参考价值。
最近看论文里面有好多凸优化、对偶函数、KKT什么的,太顶了,看不下去,就先补一补这方面的知识。
凸优化其实是一个比较大的问题,看了半天也是一知半解,只能理解大概的原理和意义,这里就先记录一下,后面有更深的理解再补充。
我们知道所谓优化就是要去找全局最优解,凸优化是什么,凸优化中的全局最优解怎么找,我们首先从一般的优化问题开始理解。
优化问题的基本形式
minimize
f
0
f_0
f0(w), w∈
R
n
R^n
Rn
subject to
f
i
f_i
fi(w)≤0, i=1,…,m;
h
j
h_j
hj(w)=0, j=1,…,p
以上式子为普通的优化问题的基本形式,其中优化变量为w∈
R
n
R^n
Rn,不等式约束为
f
i
f_i
fi(w)≤0,等式约束为
h
j
h_j
hj(w)=0。特殊情况:当m=p=0时,就变成了无约束优化问题。
相关概念:
定义域:优化问题
f
0
f_0
f0(w)的定义域D就是
f
i
f_i
fi(w)和
h
j
h_j
hj(x)定义域的交集: D = dom
f
i
f_i
fi∩dom
h
j
h_j
hj
可行点(解):若w∈D,且满足约束条件,那么x就是可行点
可行域:所有可行点的集合
最优化值:
p
∗
p^*
p∗=inf{
f
0
f_0
f0(w)|
f
i
f_i
fi(w)≤0, i=1,…,m,
h
j
h_j
hj(w)=0, j=1,…,p}
最优化值就是优化问题
f
0
f_0
f0(x)在满足约束条件时,所有函数值的下确界。
最优化解:
p
∗
p^*
p∗=
f
0
f_0
f0(
w
∗
w^*
w∗)
最优化解就是函数值为
p
∗
p^*
p∗时x的取值
w
∗
w^*
w∗。
凸优化问题的基本形式
说完了优化问题的基本形式,那凸优化问题又是怎么样的呢?首先,表达式上是一样的,都是
minimize
f
0
f_0
f0(w), w∈
R
n
R^n
Rn
subject to
f
i
f_i
fi(w)≤0, i=1,…,m;
h
j
h_j
hj(w)=0, j=1,…,p
不同之处在于,只有当
f
i
f_i
fi(w)是凸函数,
h
j
h_j
hj(w)是仿射函数时,普通的优化问题才变为凸优化问题。
这种定义有什么好处呢?当然有,只要在于
一、可行域是凸集
二、局部最优解即为全局最优解
诶,全局最优解不就是我们优化问题的目标吗?所以说,凸优化问题不用担心陷入局部最优解的情况。
问题的转化
在凸优化中,当目标函数本身比较复杂时,常将目标函数通过拉格朗日函数转换为其对偶问题进行求解,这样能够更高效地得到最优化值。这个转换的过程是怎样的呢?我们接着看下面的例子。
下面是一个一般的优化问题
P
0
P_0
P0(
f
i
f_i
fi(w)不用是凸函数,
h
j
h_j
hj(w)也不用是仿射函数)
minimize
f
f
f(w), w∈
R
n
R^n
Rn
subject to
g
i
g_i
gi(w)≤0, i=1,…,m;
h
j
h_j
hj(w)=0, j=1,…,p
假设
P
0
P_0
P0的最优解为
p
∗
p^*
p∗
通过拉格朗日乘子法将问题
P
0
P_0
P0转换为
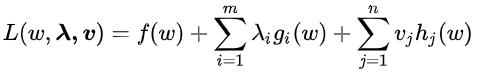
其中λ=[
λ
1
λ_1
λ1,…,
λ
m
λ_m
λm] ,且∀i,
λ
i
λ_i
λi≥0。v=[
v
1
v_1
v1,…,
v
p
v_p
vp]。
根据定义我们知道
h
j
h_j
hj(w)=0,
g
i
g_i
gi(w)≤0,所以实际上,L(w,λ,v)是关于λ的仿射函数。
再加上现在
λ
i
λ_i
λi≥0,则对于w的任意可行解都有L(w,λ,v) ≤ f(w)
回到问题
P
0
P_0
P0本身,这个优化问题的目的是找全局最优解,也就是f(w)最小值,而我们此时其实可以把问题转换成求L(w,λ,v) 的下确界(因为L(w,λ,v) ≤ f(w),所以min f(w) ≥ inf L(w,λ,v),也就可以通过L(w,λ,v) 的下确界来逼近求解f(w)的最小值)
对偶函数
而拉格朗日函数L(w,λ,v)的下确界就是拉格朗日对偶函数,简称为“对偶函数”,表示为:
g(λ,v) = inf L(w,λ,v) ≤ min f(w) =
p
∗
p^*
p∗
由L(w,λ,v)的表达式可知 g(λ,v) 关于拉格朗日乘子λ,v是线性的(因此是凹的),而inf函数是保凹的。所以即使原问题
P
0
P_0
P0不是凸的(我们这里讨论的例子只是一般的优化问题),其对偶函数g(λ,v)也是凹的。
注意了,g(λ,v)是凹的,那么只要加个负号,也就是-g(λ,v),就可以变成一个凸函数!这样我们就可以把一个一般的优化问题转化为一个凸函数求极值问题!
对偶问题
求解下确界可以定义为求解以下问题,记为
D
0
D_0
D0 以上是关于凸优化中的对偶问题的主要内容,如果未能解决你的问题,请参考以下文章
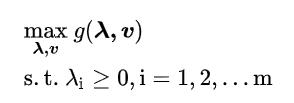
实际上
D
0
D_0
D0就是原始问题
P
0
P_0
P0的对偶问题,其最优解记为
d
∗
d^*
d∗。由之前的推导可知,
d
∗
d^*
d∗ ≤
p
∗
p^*
p∗,此时称
D
0
D_0
D0为
P
0
P_0
P0的弱对偶问题(只能通过
D
0
D_0
D0的最优化解去逼近
P
0
P_0
P0的最优化解),而当
d
∗
d^*
d∗ =
p
∗
p^*
p∗时,就称
D
0
D_0
D0为
P
0
P_0
P0的强对偶问题(此时
D
0
D_0
D0的最优化解就是
P